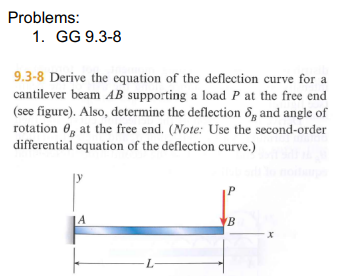
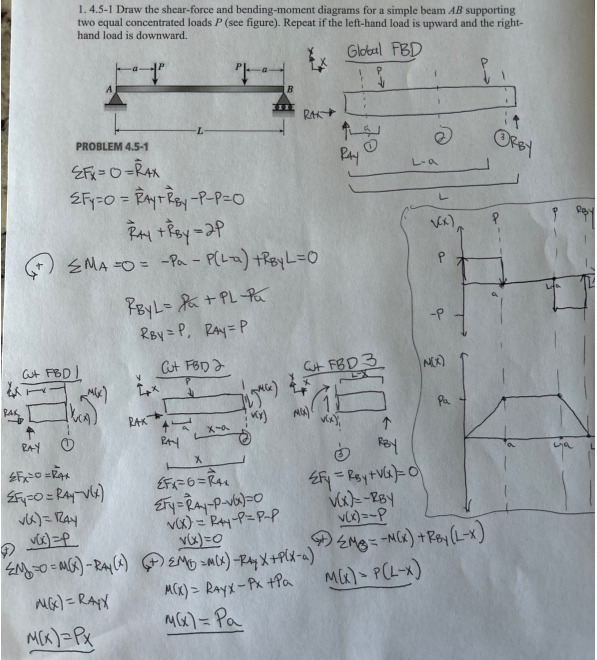
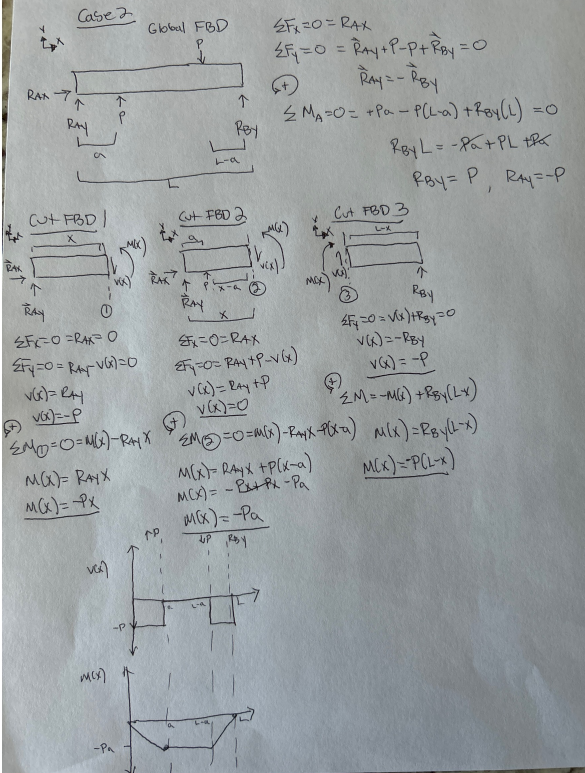
Problems: 1. GG 9.3-8 9.3-8 Derive the equation of the deflection curve for a cantilever beam AB supporting a load P at the free end (see figure). Also, determine the deflection do, and angle of rotation at the free end. (Note: Use the second-order differential equation of the deflection curve.) A L B x 1.4.5-1 Draw the shear-force and bending-moment diagrams for a simple beam AB supporting two equal concentrated loads P (see figure). Repeat if the left-hand load is upward and the right- hand load is downward. Global FBD P II B RAK PAY Cut FBD PROBLEM 4.5-1 Fx =0=RAX 2Fy=0=Ray+Rey-P-P=0 MA== -Pa-P(La) +Rey L=0 RBYL= a + PL-Pa RBY = P, RAY = P Cut FBD2 ORBY L-a VCX) P P -P Cut FBD3 NOX) MW) Pa x19 RAK 4 RAY FX0=R4x Fy=0 = Ray-v(x) RAX RAY EFX=6=R4x RBY y=Ray+Vx=0 V(x)=-2BY (x)=RAY v(x) = Ray-P=P-P v(x)=0 v(x)=-P Mg=-M(x) +Rey (L-X) 0=M)-RAY() EM=M(x)-RX+P(x-a) M(x)=RAYX MCX)= RAYX-Px +Pa M(X) = P(L-X) M(x)=Px MGX)= Pa Case 2 Global FBD Fx =0=RAX RAX 7 RAY 7 Rey L-a Cut FBD Cut FBD 2 2y=0 = Ray+P-P+Ray = 0 RAY=-RBY + MA== +Pa - P(La) +284(L)=0 RBY L= -Pa+PL the Cut FBD3 L-X RBY= P, RAY=-P RAY FX=0=RAX y=0= RAVGx)=0 V(x)=RAY VG)=-P EMO=0=MX-RAYX M(X)= RAYX M(x)=Px VG) RAK RAY + SEX=0=RAX 2y=0= RAY+P-V (x) v(x)= Ray +P v(x)=0 1 MCX vu)." RBY 24=0=(x)+3y=0 V(x)=-RBY v(x) = -P M=-MG) +RBy(Lx) M=0=M(x)-RayX-P(xa) M(x)=R8y(L-x) M(x)= RAYX +P(x-a) MCX)= -PP-Pa MCX)=-PCL-X) M(x)=-Pa UP Y M(x) -Pa