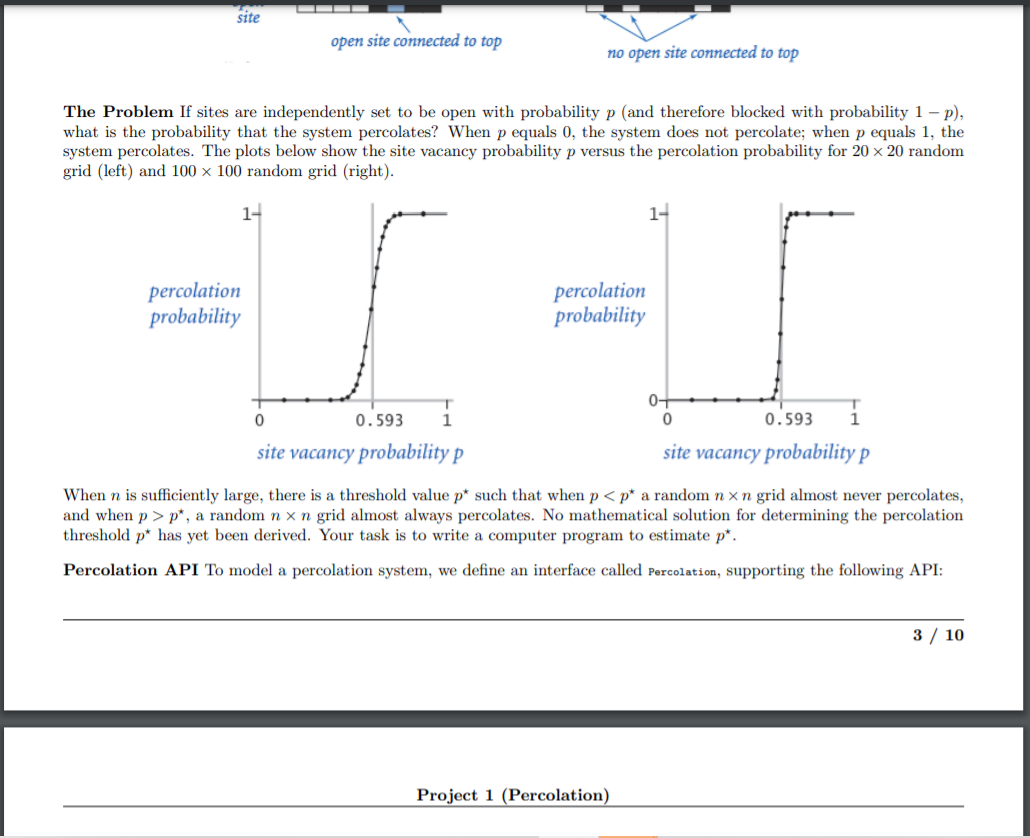
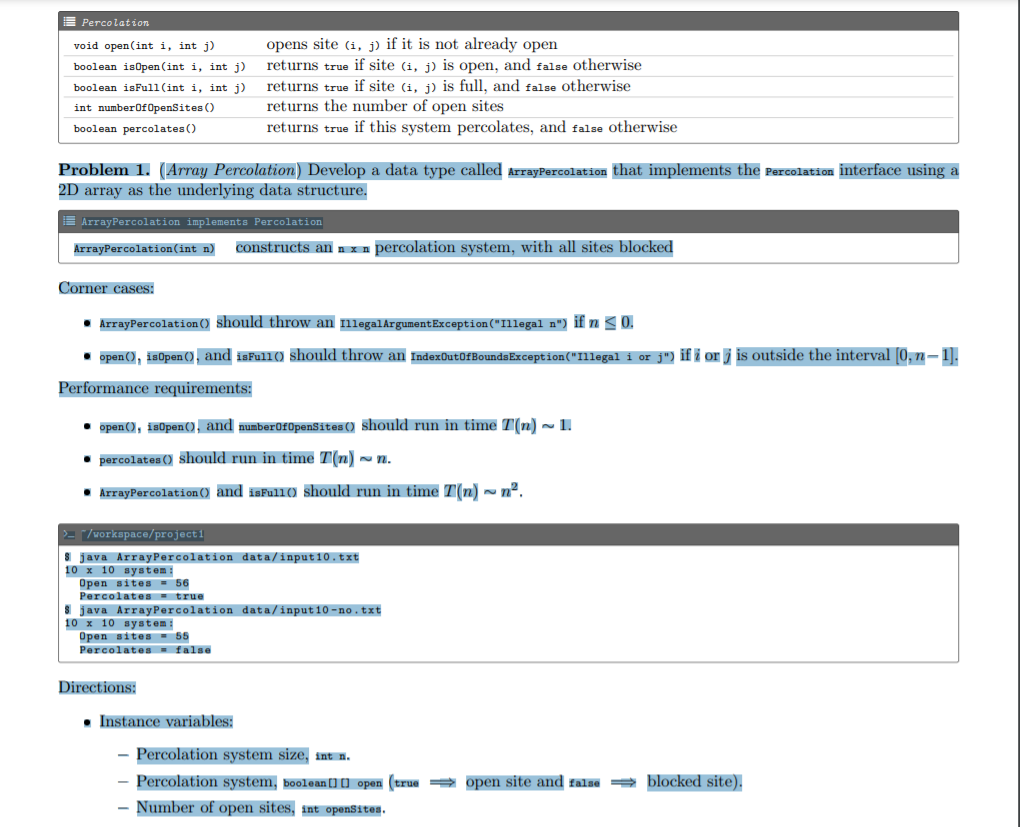
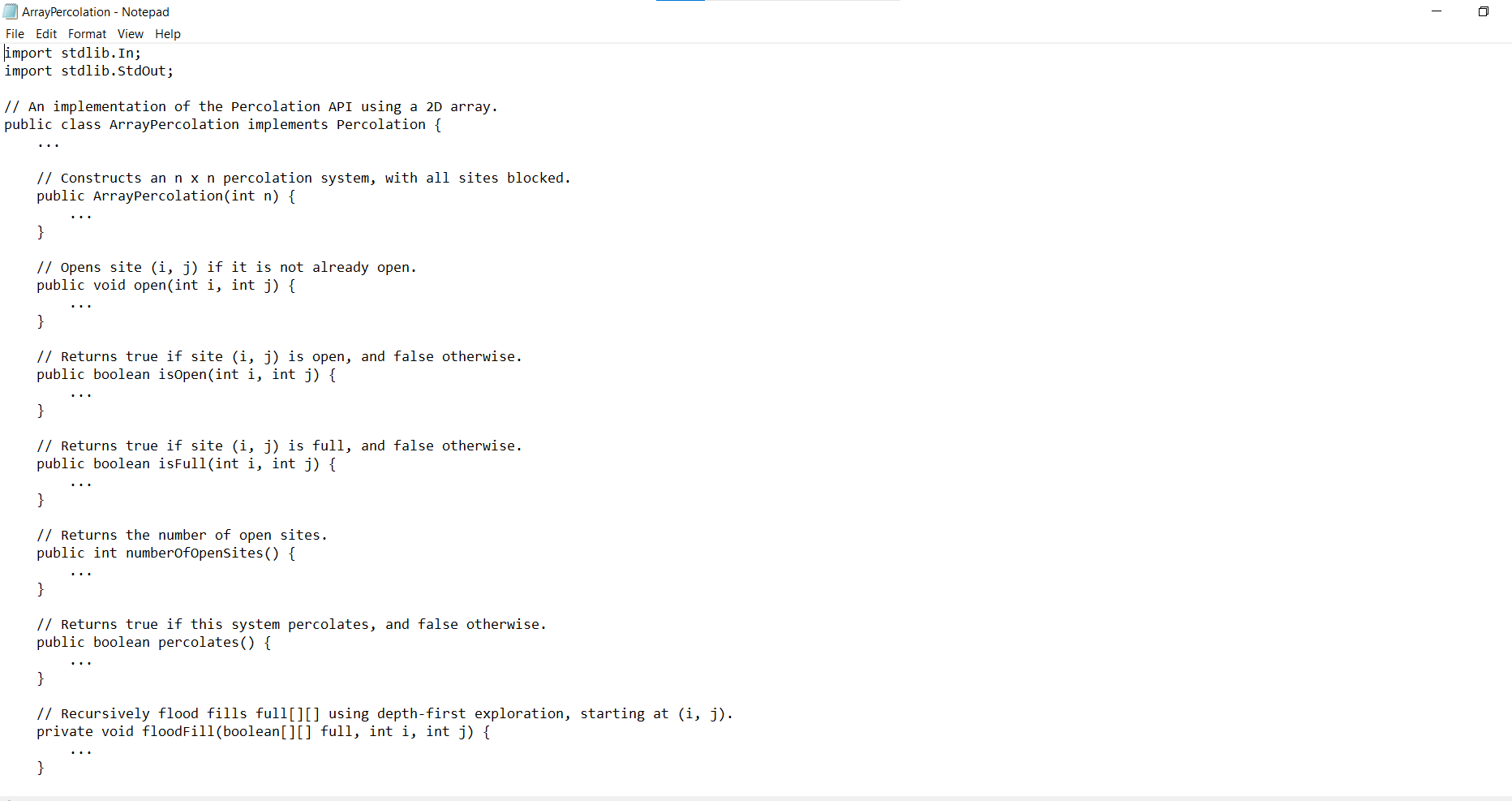
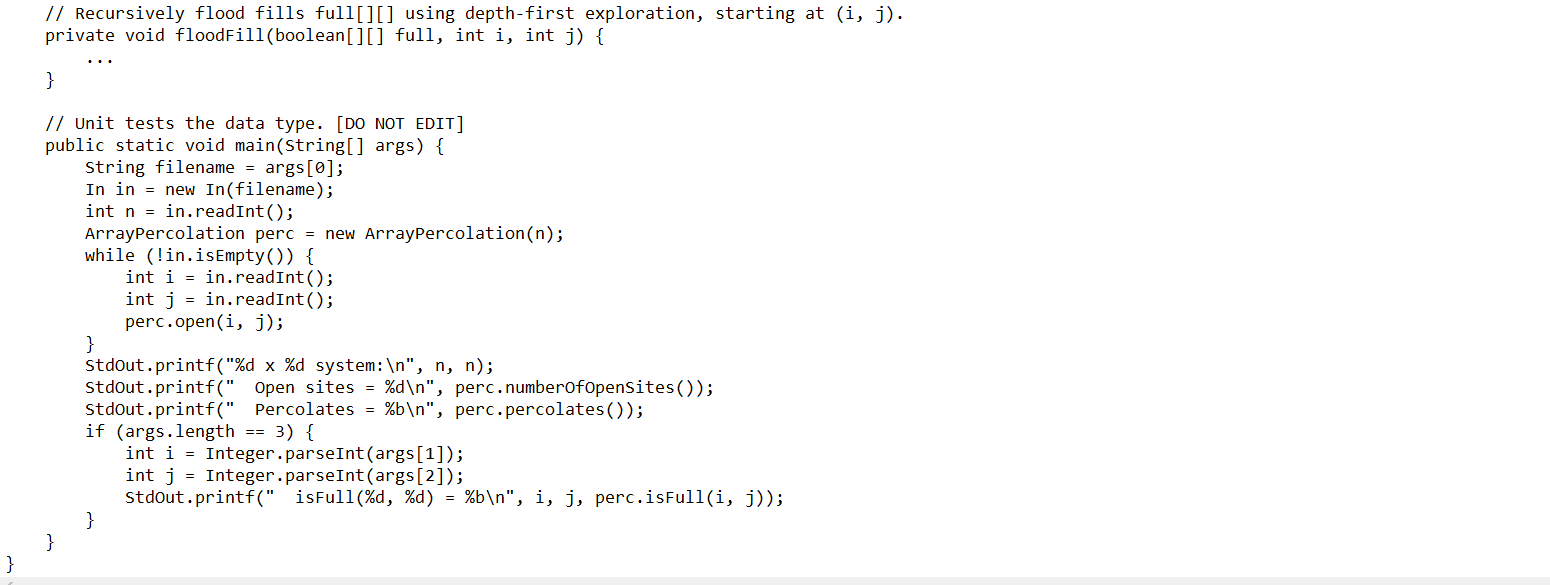
Problems Goal Write a program to estimate the percolation threshold of a system. Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations. Project 1 (Percolation) The Model We model a percolation system using an nan grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. percolates does not percolate empty open site 1- blocked site full open site open site connected to top no open site connected to top The Problem If sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20 x 20 random grid (left) and 100 x 100 random grid (right). 1- site 1- open site connected to top The Problem If sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20 x 20 random grid (left) and 100 x 100 random grid (right). percolation probability no open site connected to top 0 0.593 1 site vacancy probability p percolation probability 1- Project 1 (Percolation) 0- 0 0.593 1 site vacancy probability p When n is sufficiently large, there is a threshold value p* such that when p < p* a random nxn grid almost never percolates, and when p > p*, a random n x n grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*. Percolation API To model a percolation system, we define an interface called Percolation, supporting the following API: 3/10 Percolation void open(int i, int j) boolean isOpen (int i, int j) boolean isFull (int i, int j) int number Of OpenSites () boolean percolates () Problem 1. (Array Percolation) Develop a data type called ArrayPercolation that implements the Percolation interface using a 2D array as the underlying data structure. ArrayPercolation implements Percolation ArrayPercolation(int n) constructs anx percolation system, with all sites blocked Corner cases: opens site (i, j) if it is not already open returns true if site (i, j) is open, and false otherwise returns true if site (i, j) is full, and false Otherwise returns the number of open sites returns true if this system percolates, and false otherwise ArrayPercolation() should throw an Illegal ArgumentException ("Illegal n") if n < 0. open(), isOpen(), and isFul10 should throw an IndexOutOfBounds Exception ("Illegal i or j") ifi orj is outside the interval [0, n1]. Performance requirements: open(), isOpen(), and numberOfOpenSites() should run in time T(n) 1. percolates() should run in time T(n) n. ArrayPercolation () and isFull should run in time T(n) ~ n. > "/workspace/project1 Sjava ArrayPercolation data/input10.txt 10 x 10 system: Open sites = 56 Percolates = true Sjava ArrayPercolation data/input10-no.txt 10 x 10 system: Open sites = 55 Percolates = false Directions: Instance variables: - Percolation system size, int n. - Percolation system, boolean[] [] open (true open site and false blocked site). - Number of open sites, int openSites. Instance variables: Percolation system size, int n. Percolation system, boolean[] [] open (true open site and false blocked site). Number of open sites, int openSites. private void floodFill(boolean[][] full, int i, int j) - Return if i orj is out of bounds; or site (i, j) is not open; or site (i, j) is full (ie, full[i][j] is true). - Fill site (i, j). - Call floodFi110) recursively on the sites to the north, east, west, and south of site (i, j). public ArrayPercolation (int n) - Initialize instance variables. void open(int i, int j) If site (i, j) is not open: * Open the site. * Increment opensites by one. Project 1 (Percolation) boolean isOpen(int i, int j) - Return whether site (1, 3) is open or not. boolean isFull(int i, int j) - Create an n x n array of booleans called fu11. - Call floodFill() on every site in the first row of the percolation system, passing run as the first argument. 4/ 10 boolean isFull(int i, int j) - Create an n x n array of booleans called full. - Call floodF111() on every site in the first row of the percolation system, passing full as the first argument. - Return full [1] [j]. int number of OpenSites () - Return the number of open sites. boolean percolates() - Return whether the system percolates or not a system percolates if the last row contains at least one full site. ArrayPercolation - Notepad File Edit Format View Help import stdlib.In; import stdlib.stdout; // An implementation of the Percolation API using a 2D array. public class ArrayPercolation implements Percolation { // Constructs an n x n percolation system, with all sites blocked. public ArrayPercolation (int n) { } // Opens site (i, j) if it is not already open. public void open(int i, int j) { } // Returns true if site (i, j) is open, and false otherwise. public boolean isopen(int i, int j) } // Returns true if site (i, j) is full, and false otherwise. public boolean isFull(int i, int j) { } // Returns the number of open sites. public int numberOfOpenSites() { } // Returns true if this system percolates, and false otherwise. public boolean percolates () { } // Recursively flood fills full[][] using depth-first exploration, starting at (i, j). private void flood Fill (boolean[][] full, int i, int j) { } I 0 // Recursively flood fills full[][] using depth-first exploration, starting at (i, j). private void floodFill(boolean[][] full, int i, int j) { } // Unit tests the data type. [DO NOT EDIT] public static void main(String[] args) { String filename = args[0]; } In in = new In (filename); int n = in.readInt (); ArrayPercolation perc = new ArrayPercolation (n); while (!in.isEmpty()) { int i = in.readInt (); int j = in.readInt (); perc.open(i, j); } stdout.printf("%d x %d system: ", n, n); stdout.printf(" Open sites = %d ", perc.numberOfOpenSites ()); stdout.printf(" Percolates = %b ", perc.percolates()); if (args.length == 3) { int i = Integer.parseInt(args[1]); int j = Integer.parseInt(args[2]); stdout.printf(" isFull(%d, %d) = %b ", i, j, perc.isFull(i, j));