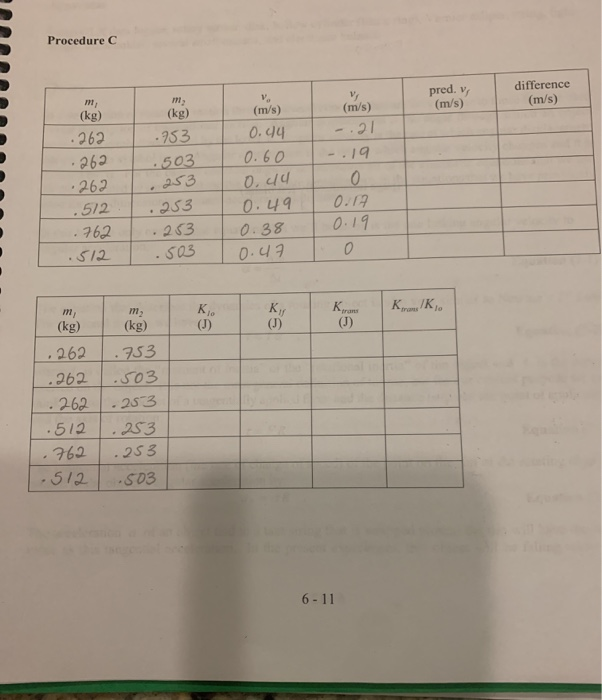
Procedure C m (kg) .262 262 262 .512 762 .512 m (kg) .753 503 .253 .253 .253 -503 m (kg) (kg) .262 .753 .262 .503 .262 1.253 .512 .253 -762 .253 512 .503 Klo 6 V (m/s) 0.44 0.60 0.44 0.49 0.38 0.47 K (m/s) -.21 -.19 0 0.17 0.19 0 Karamanis (J) 6-11 pred. v, (m/s) Krans Ko difference (m/s) In the case of a completely inelastic collision, the objects join together and move as one after the collision. For a completely inelastic collision in which the target is initially at rest, conservation of momentum may be expressed by: mv, Mv Equation (6-4) after is the mass of the initially moving object, v, is its velocity, Mis the mass of the combined object after the collision, and v, is the velocity of the combined object. Equation (6-4) can be solved for any one of the quantities that appear in it if all of the others are known. this experiment we ll use it to obtain predicted final velocities, which will be compared to observed final In completely inelastic collisions, and in many collisions that are not completely inelastic, kinetic energy belost. [It is also possible to have a collision in which kinetic energy is gained; consider the collision between a pop ball and the pavement.] Collisions in which the kinetic energy of the system after the collision is the same as the system kinetic energy was before the collision are called elastic collisions. In all elastic collisions, the individual objects remain separate. Thus, the conservation-of-momentum equation contains more terms. Again considering the case for which one object is initially at rest, we will now have: MVMV// Equation (6-5) The additional requirement that is imposed on elastic collisions, conservation of kinetic energy, may be expressed as: m - + m, ++ mv, Equation (6-6) In our experiment, we will be monitoring the velocity of the initially-moving object. In order to be able to compare our experimental results with the predictions of theory, we need to obtain the final velocity of mass 1 from these two equations. First, solve Equation (6-5) for v. This produces: V/ = V M Substitute this result into Equation (6-6) and multiply all terms by 2. From this we obtain: my-mv, + M The equation can be rewritten: (-)--- The difference of squares factors into the product of the sum and the difference. Then, the difference term can be cancelled to produce: 6-2 . m M VI and this can be re-organized to give us: (m, +m,)v,, (m, -m,)v,, which can then be solved for the final velocity of object 1 . The result is: AM+ AM Equation (6-7) We will compare values predicted by this equation to our experimental values of the final velocities. Additional Kinematic Theory Used in the Analysis The following section does not relate to energy or momentum conservation but is needed for the analysis of the data used in the first part of this lab. We use one of the standard one-dimensional constant-acceleration kinematic equations to analyze our raw data in this lab. We need: v+2a(d-d.) Equation (6-8) where d is the position along some scale, v, is the initial velocity, a is the constant acceleration, and ris the time since the object had its initial position and velocity. For our experiment, the object will be released from rest so v, is zero. Replace the difference in positions with D (for distance traveled) and solve for v (taking into account that the initial velocity is zero) to obtain: Equation (6-9) v=2aD which gives us the velocity at the end of the object s path. We will also use the definition of acceleration (for the case of constant acceleration) in our analysis. Note Concerning the Previous Section and the Operation of the Motion Sensor In this lab a motion sensor is used in all three sections (energy conservation, inelastic collisions, and elastic collisions). This sensor, used in conjunction with the GLX data logger, is capable of providing data in the form of position vs. time, velocity vs. time, or acceleration vs. time. Its operation, however, is such that it really only determines position. The internal software in the GLX computes velocity or acceleration from that position data. The motion sensor is a pulse-echo device. It emits a sequence of ultrasonic signals and listens for their returns. It is then a simple matter to determine the position of the object being observed as a function of time. Velocity calculations are done by dividing differences in two successive positions by the differences in the times at which those positions occurred. Acceleration calculations are done by dividing differences in two successive velocity calculations by the differences in the times at which those occurred. 6-3 Procedure C 28. Transfer the masses back to the red car and place the cars back on the track, located as in step 19 but now with the red car s Velcro pads toward the bumper and the blue car s Velcro pads toward the sensor. The other ends of the cars have magnetic bumpers that should repel one another. Now the collision will be approximately elastic. 6-6 29. Repeat the data collection process used in Procedure B. [Steps 20-24, except see the following statement regarding the graph on screen.] The graph during this procedure may look like the one displayed previously for Procedure B or it may look like the one in Figure (6-2) at right. The difference between this graph and the previous one is that the final velocity is negative. [Recall that the dotted line is the 0 reference line for velocity.] Figure 6-2 30. Use Equation (6-7) to find predicted final velocities. Also, find the differences (not percentage differences) between these values and the measured velocities. 31. Copy the masses to the appropriate locations in the next table. For each run, find the initial and final kinetic energies of car 1 (the blue car). [Note that the kinetic energy in this case is not lost from the system but transferred to the other (red) car.] The initial energy of the blue car is: and the final energy of the blue car is: 32. Calculate the amount of energy transferred from the blue car to the red car. Also, calculate the ratio of the transferred energy to the initial kinetic energy of the blue car. 33. Straighten up your area, turn off the GLX, and submit your lab report to your lab instructor.