Programming Language C++

What kind of logic is similar to list of children implementation?

(btw this is list of children implementation)

a) Breadth-first tree traversals

b) Depth-first tree traversals

c) pre-order

d) post-order

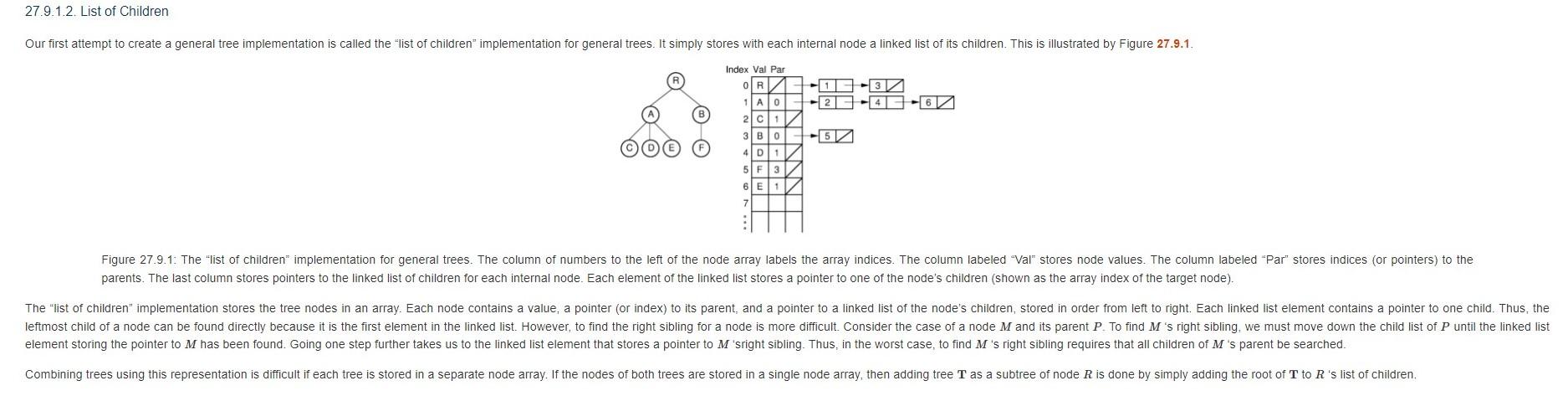
27.9.1.2. List of Children Our first attempt to create a general tree implementation is called the "list of children" implementation for general trees. It simply stores with each internal node a linked list of its children. This is illustrated by Figure 27.9.1 Index Val Par R A 0 3 -11 -23 21 C 11 3 B 0 -54 4D1 5 F 3 6E 1 Figure 27.9.1: The "list of children" implementation for general trees. The column of numbers to the left of the node array labels the array indices. The column labeled "Val" stores node values. The column labeled "Par" stores indices (or pointers) to the parents. The last column stores pointers to the linked list of children for each internal node. Each element of the linked list stores a pointer to one of the node's children (shown as the array index of the target node). The "list of children" implementation stores the tree nodes in an array. Each node contains a value, a pointer (or index) to its parent, and a pointer to a linked list of the node's children, stored in order from left to right. Each linked list element contains a pointer to one child. Thus, the leftmost child of a node can be found directly because it is the first element in the linked list. However, to find the right sibling for a node is more difficult. Consider the case of a node M and its parent P. To find M's right sibling, we must move down the child list of P until the linked list element storing the pointer to M has been found. Going one step further takes us to the linked list element that stores a pointer to M'sright sibling. Thus, in the worst case, to find M's right sibling requires that all children of M's parent be searched. Combining trees using this representation is difficult if each tree is stored in a separate node array. If the nodes of both trees are stored in a single node array, then adding tree T as a subtree of node R is done by simply adding the root of T to R's list of children