Prove every linear combination of sa + tb can be accurately measured using jugs of capacities a, b. It is required that 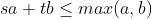, since the measured amount must fit within one of the jugs. Assume that a

a. Show that if m is a linear combination of a, b then m = sa + tb where s > 0. In other words, every linear combination can be expressed in a manner where the coefficient of the smaller jug is non-negative.

Hint: what happens to the value of the linear combination if we increase s to s+b and decrease t to t-a?

b. Consider the following algorithm, starting with two empty jugs A of capacity a, and B of capacity b, with a

1. Fill jug A.

2. Pour as much water from A into B as possible. If B becomes full, empty it out, and finish pouring any remaining water from A into B.

Show the sequence of states (amount in each jug) at each step if a = 21 and b = 26 until jug B contains exactly 3 units of water. Here are the first few steps:

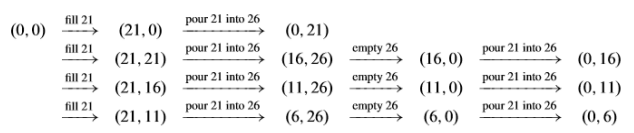
c. Show that when the algorithm is repeated s times, where s satisfies the conditions of part (a) above, that the amount of water in jug B is exactly m. The remarkable conclusion is that not only can every multiple of gcd(a,b) be measured eactly, but we don't even need to know s and t in advance. Simply repeat the 2-step algorithm until you have the desired amount in jug B.

sa tb S mar (a, b) sa tb S mar (a, b)