Question: . Prove that these inference rules are sound. . Are these inference rules complete? If so, then prove why. Otherwise, show why not. HINT:

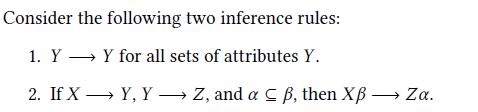
. Prove that these inference rules are sound. . Are these inference rules complete? If so, then prove why. Consider the following two inference rules: 1. Y Y for all sets of attributes Y. 2. If XY, Y Z, and a B, then

. Prove that these inference rules are sound. . Are these inference rules complete? If so, then prove why. Otherwise, show why not. HINT: You may assume that the Armstrong Axioms are complete. . Are these inference rules independent? If so, then show why. Otherwise, show why not. Consider the following two inference rules: 1. Y Y for all sets of attributes Y. 2. If XY, Y Z, and a B, then XB Za.

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Lets analyze the given inference rules one by one in terms of soundness completeness and independence 1 YY for all sets of attributes Y Soundness This ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

WATCH DOCUMENTARY: https://youtu.be/V3kJ6OticrY Questions: 1. What insights did you gain from watching the documentary? List and explain at least three. Timestamp each point from the video. 2. For...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Laura Martinez is interested in buying and selling soybeans on the Chicago Board of Trade. She remembers that they discussed concepts like price functions, revenue functions, cost functions, profit...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Microkernel operating systems aim to address perceived modularity and reliability issues in traditional "monolithic" operating systems. (i) Describe the typical architecture of a microkernel...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Assume all rates are annualized with semi-annual compounding. Be explicit about how you derive your results and round to four decimals after the comma. The 0.5-year zero rate is 7% and the 1-year...

Born in the rural area of Mbale, Uganda, Andrew Mupuya moved to Kampala on a half bursary to study at an advanced level. It later became a hurdle to cater for his needs while at school after his...

In finance managament this is question ehre Use excel for frollowing question . Carling Corporation will raise $ 1 , 0 0 0 , 0 0 0 to finance an expansion. They plan to raise $ 5 0 0 , 0 0 0 through...

For each relation given below determine whether it is reflexive, irreflexive or neither; symmetric, asymmetric, antisymmetric, or none of the above; transitive or not. Rom this determine whether it...

The solubility of a solid solute in four different solvents is shown in the graph below. Based on the information in the graph, selected the best solvent to use for a recerystallization of this...

A stone, M= 1 kg is projected from a point, h= 15 m above the ground with an initial speed, v - 10 m/s. What is the speed of the stone, v just before it strikes the ground? (assume g = 10 m/s, ignore...

A 90 kg man on ice skates pushes and a 50 kg boy on skates with a force of 60 N. The magnitude of the force exerted by the boy on the man is, OA) 60 N B) 900 N 50 N D) 90 N E) 600 N

If the total work done on a particle is negative, what happens to its kinetic energy? O A) Its kinetic energy increases. B) Its kinetic energy does not charnge OC) Its kinetic energy become negative....

Paula is a freelance accountant hired by George's Fried Chicken whenever auditing work is needed in the back office. Paula is called to the office on a need basis and is paid $250 per day for her...

The circuit in Figure 5.59 gives a shift register in which the parallel load control input is independent of the enable input. Show a different shift register circuit in which the parallel-load...

Section 7.5 shows how to implement the traditional long division that is done by hand. A different approach for implementing integer division is to perform repeated subtraction as indicated in the...

Convert the following binary numbers into decimal. (a) (1001) 2 (b) (11100) 2 (c) (111111) 2 (d) (101010101010) 2

An analyst has timed a metal-cutting operation for 50 cycles. The average time per cycle was 10.40 minutes, and the standard deviation was 1.20 minutes for a worker with a performance rating of 125...

How are tools such as a process chart and a worker-machine chart useful?

How many work cycles should be timed to estimate tire average cycle time to within 2 percent of the sample mean with a confidence of 99 percent if a pilot study yielded these times (in minutes): 5.2,...