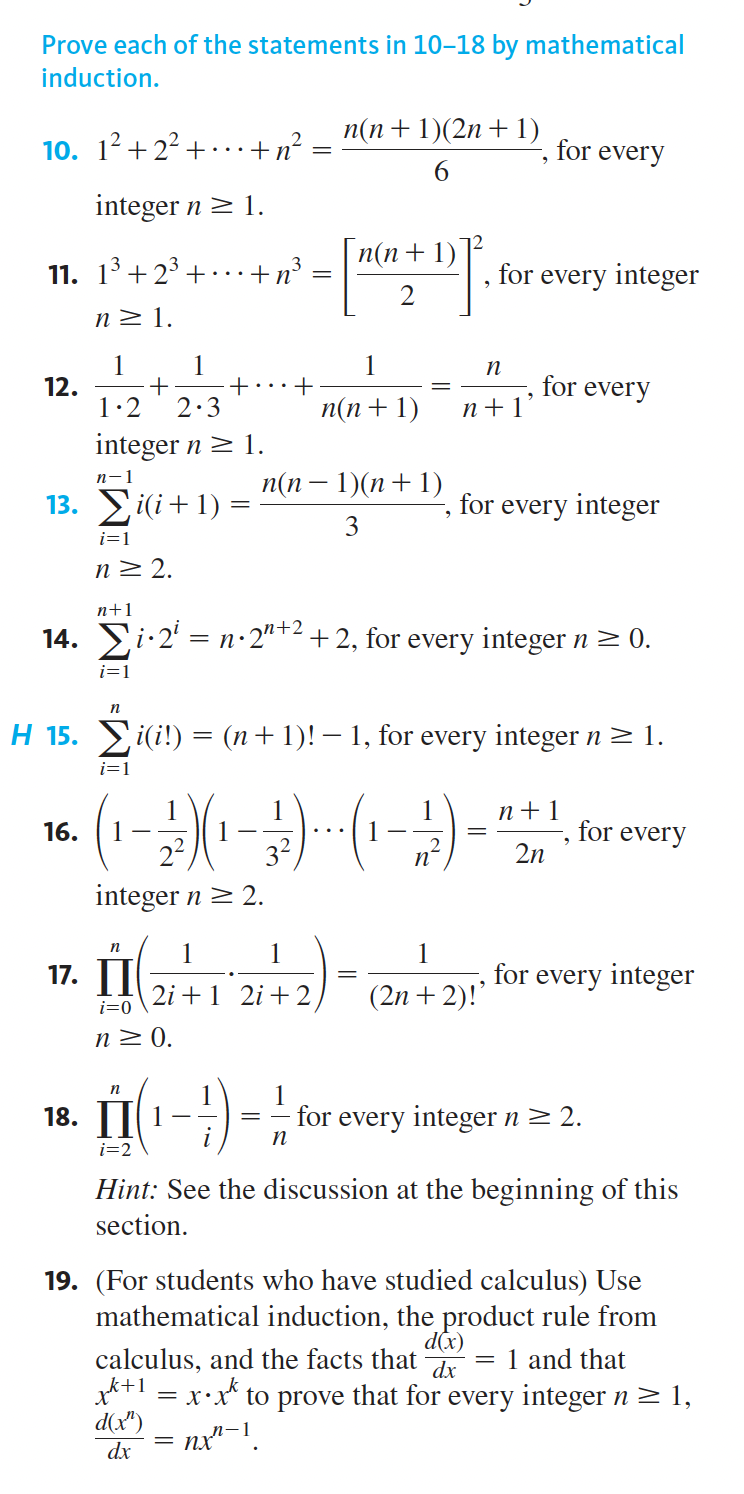
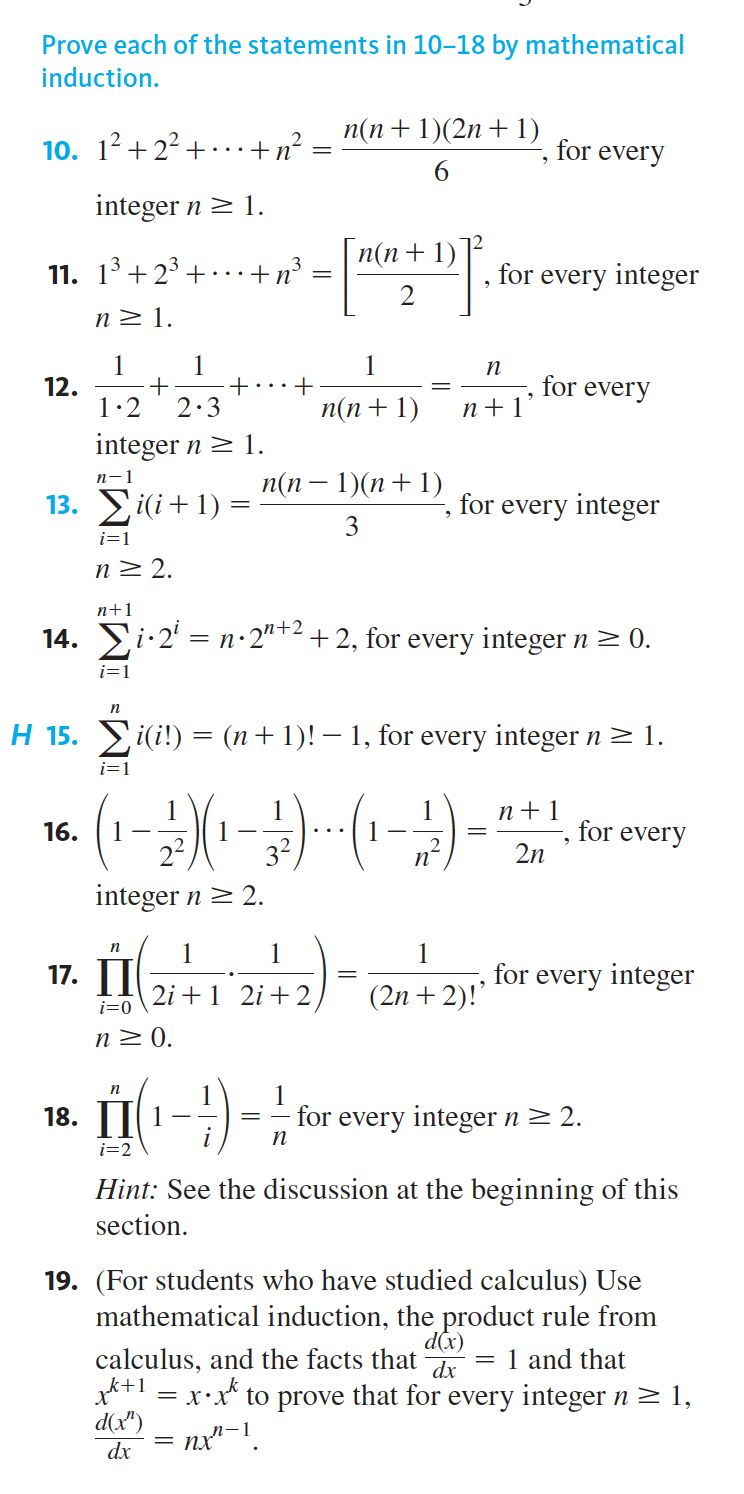
Prove the statements in 111. In each case use only the definitions ofthe terms and the Assumptions listed on page 161, not any previously established properties of odd and even integers. Follow the directions given in this section for writing proofs of universal statements. 1. For every integer n, if n, is odd then 3;: + 5 is even. 2. For every integer m, if m is even then 3171 + 5 is odd. 3. For every integer n, 2n 1 is odd. 4. Theorem 4.2.2: The difference of any even inte ger minus any odd integer is odd. In 1720, determine whether the property is true for all integers, true for no integers, or true for some integers and false for other integers. Justify your answers. 17. (a+b)2 = 613+};2 ac a+c w.+= Prove each statement in 6-9 using mathematical induction. Do not derive them from Theorem 5.2.2 or Theorem 5.2.3. 6. For all integers n > 1, 2 + 4 + 6 + . .. + 2n = n- + n. 7. For all integers n 2 1, n(5n - 3) 1 + 6+ 11 + 16 + . .. + (5n -4) = 2 8. For all integers n 2 0, 1 + 2 + 22 + ... + 2" = 2n+1 - 1. 9. For all integers n > 3, 4(4" - 16) 4 + 45 + . . . + 4n = 3Prove each of the statements in 10-18 by mathematical induction. 10. 12 + 22 + .. . + 12 = n(n + 1)(2n + 1) , for every 6 integer n 2 1. n(n + 1) 72 11. 13 + 23 + .. . + n) = , for every integer 2 n 21. 1 n 12. + .. .+ for every 1 .2 2.3 n(n + 1) n+1 integer n 2 1. n- 1 13. Ci(i + 1) n(n - 1)(n + 1) for every integer i=1 3 n 2 2. n+1 14. i.2' = n. 2"+2 + 2, for every integer n 2 0. i=1 n H 15. i(i!) = (n + 1)! -1, for every integer n 2 1. 1= 1 n +1 16. = for every n 2n integer n > 2. n 17. II for every integer 1=0 2i + 1 2i + 2 (2n + 2)!' n 20. n 18. - for every integer n > 2. i=2 n Hint: See the discussion at the beginning of this section. 19. (For students who have studied calculus) Use mathematical induction, the product rule from calculus, and the facts that d = 1 and that d(x) *+l = x.x to prove that for every integer n 2 1, d(x") = nx-1.Some of the statements in 1522 are true and some are false. Prove each true statement and find a counterexarr ple for each false statement, but do not use Theorem 4.6 in your proofs. 15. For every real number x, [x 1] = LxJ 1. 16. For every real number x, [162] = m2. H 17. For every integer n, 12/3 ifn mod 3 = 0 [31/3]: (n1)/3 ifnm0d3 =1 (n2)/3 ifnm0d3=2. H 18. For all real numbers x and y, [x + y] = [x] + [y]. H 19. For every real number x, [x 1] = [x] 1