Provide code BY ENTERING CODE WHERE IT STATES "# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****" 

(Table 5.1 is at the end of the problems)
 

# set up code for this experiment
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

np.random.seed(1)
 

Problem 1: Exercise 4.1 of Alpaydin {-}

Write the code that generates a Bernoulli sample with given parameter p, and the code that calculates p from the sample. You can choose any data structure to store the samples.

def ex4_1(p, nSample):
"""

  Inputs:
  - p: the parameter of Bernoulli
  - nSample: number of samples to draw
 
Output:
  """
  np.random.seed(1)
 
  # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  return phat
 

Problem 2: Exercise 4.3 of Alpaydin {-}

Write the code that generates a real-valued normal sample with given μ and σ, and the code that calculates m and s from the sample. Do the same using the Bayes' estimator assuming a Gaussian prior distribution for μ.

def ex4_3_mle(mu, sigma, nSample):
  """
  find the labels of the top k nearest neighbors
 
  Inputs:
  - mu: mean of Gaussian
  - sigma: standard deviation of Gaussian
  - nSample: number of samples to draw
 
  Output:
  - m:
  - s:
  """
  np.random.seed(1)
 
  # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  return m, s
 
def ex4_3_Bayes(mu, sigma, priorMean, priorStd, nSample):
  """
 
  Inputs:
  - mu: mean of Gaussian
  - sigma: standard deviation of Gaussian
  - priorMean: the mean of the Gaussian prior assumed on mu
  - priorStd: the standard deviation of the Gaussian prior assumed on mu
  - nSample: number of samples to draw
 
  Output:
  - m:
  - s:
  """
  np.random.seed(1)
 
  # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  return m, s
 

Problem 3: Exercise 4.6 of Alpaydin {-}
For a two-class problem, generate normal samples for two classes with different variances, then use parametric classification to estimate the discriminant points. Compare these with the theoretical values.

def ex4_6(X_test, X_train, Y_train, k):
  """
  predict labels for test data.
 
  Inputs:
  - X_test: A numpy array of shape (num_test, dim_feat) containing test data.
  - X_train: A numpy array of shape (num_train, dim_feat) containing training data.
  - Y_train: A numpy array of shape (num_train) containing ground truth labels for training data
  - k: An integer, k nearest neighbors
 
  Output:
  - Y_pred: A numpy array of shape (num_test). Predicted labels for the test data.
  """
 
  num_test = X_test.shape[0]
  Y_pred = np.zeros(num_test, dtype=int)
  dists = euclidean_dist(X_test, X_train)
  neighbors = find_k_neighbors(dists, Y_train, k)
 
  for i in range(num_test):
    value, counts = np.unique(neighbors[i], return_counts=True)
    idx = np.argmax(counts)
    Y_pred[i] = value[idx]
   
  return Y_pred
 

Problem 4: Exercise 4.7 of Alpaydin {-}

Assume a linear model and then add 0-mean Gaussian noise to generate a sample. Divide your sample into two as training and validation sets. Use linear regression using the training half. Compute error on the validation set. Do the same for polynomials of degrees 2 and 3 as well.

def ex4_7(ypred, ytrue):
     """
     xxx.
     Inputs:
     - ypred: array of prediction results.
     - ytrue: array of true labels.
       ypred and ytrue should be of same length.
     Output:
     - error rate: float number indicating the error in percentage
                   (i.e., a number between 0 and 100).
"""

     error_rate =  (ypred != ytrue).mean()*100
     return error_rate
 

Problem 5: Exercise 5.2 of Alpaydin {-}
Generate a sample from a 2-dimensional normal density N(μ, Σ), calculate m and S, and
compare them with μ and Σ. Check how your estimates change as the sample size changes. Specificially, draw N = 10, 50, 500 samples. For each value of N , generate a scatter plot of
the samples drawn. On each plot, also include a contour of the original density N (μ, Σ). You can use L2 error on μ estimation, and Frobenius distance for Σ estimation.

def ex5_2(num_examples, n):
     """
     Split the dataset in to training sets and validation sets.
     Inputs:
     - num_examples: Integer, the total number of examples in the dataset
     - n: number of folds
     Outputs:
     - train_sets: List of lists, where train_sets[i] (i = 0 ... n-1) contains
                   the indices of examples for training
     - validation_sets: List of list, where validation_sets[i] (i = 0 ... n-1)
                   contains the indices of examples for validation
     """
     
     # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
     
     # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
  return train_sets, validation_sets
 
# Unit test code here (you can uncomment the lines below to test)
# train_sets, val_sets = split_nfold(11, 5)
# print(train_sets[4])
# print(val_sets[4])
 

Problem 6: Exercise 5.3 of Alpaydin {-}
Generate samples from two multivariate normal densities N(μi, Σi), i = 1, 2, and calculate the Bayes' optimal discriminant for the four cases in Table 5.1

def ex5_3(classifier, X, Y, n, *args):
  """
  Perform cross validation for the given classifier,
      and return the cross validation error rate.
  Inputs:
  - classifier: function of classification method
  - X: A 2-D numpy array of shape (num_train, dim_feat), containing the whole dataset
  - Y: A 1-D numpy array of length num_train, containing the ground-true labels
  - n: number of folds
  - *args: parameters needed by the classifier.
        In this assignment, there is only one parameter (k) for the kNN clasifier.
        For other classifiers, there may be multiple paramters.
        To keep this function general,
        let's use *args here for an unspecified number of paramters.
  Output:
  - error_rate: a floating-point number indicating the cross validation error rate
  """
  # Here is the pseudo code:
 
  np.random.seed(1)
  # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
 
  return error_rate
 
# Unit test code here (you can uncomment the lines below to test) # X_dataset = np.array([[1, 2], [0, 3], [-1, 1], [-1, 0], [2, 1]]) # Y_dataset = np.array([1, 1, 1, 0, 0])
#n= 5
#k= 3
# cross_validation(knn_predict, X_dataset, Y_dataset, n, k)
 

Problem 7: Exercise 5.6 of Alpaydin {-}

Let us say in two dimensions, we have two classes with exactly the same mean. What type of boundaries can be defined?

import os
import gzip

DATA_URL = 'http://yann.lecun.com/exdb/mnist/'

# Download and import the MNIST dataset from Yann LeCun's website.
# Each image is an array of 784 (28x28) float values  from 0 (white) to 1 (black).
def load_data():
    x_tr = load_images('train-images-idx3-ubyte.gz')
    y_tr = load_labels('train-labels-idx1-ubyte.gz')
    x_te = load_images('t10k-images-idx3-ubyte.gz')
    y_te = load_labels('t10k-labels-idx1-ubyte.gz')
   
    return x_tr, y_tr, x_te, y_te
   
def load_images(filename):
    maybe_download(filename)
    with gzip.open(filename, 'rb') as f:
        data = np.frombuffer(f.read(), np.uint8, offset=16)
    return data.reshape(-1, 28 * 28) / np.float32(256)
   
def load_labels(filename):
    maybe_download(filename)
    with gzip.open(filename, 'rb') as f:
        data = np.frombuffer(f.read(), np.uint8, offset=8)
    return data
   
# Download the file, unless it's already here.
def maybe_download(filename):
    if not os.path.exists(filename):
        from urllib.request import urlretrieve
        print("Downloading %s" % filename)
        urlretrieve(DATA_URL + filename, filename)
       
Xtrain, ytrain, Xtest, ytest = load_data()

train_size = 10000
test_size  = 10000

Xtrain = Xtrain[0:train_size]
ytrain = ytrain[0:train_size]

Xtest = Xtest[0:test_size]
ytest = ytest[0:test_size]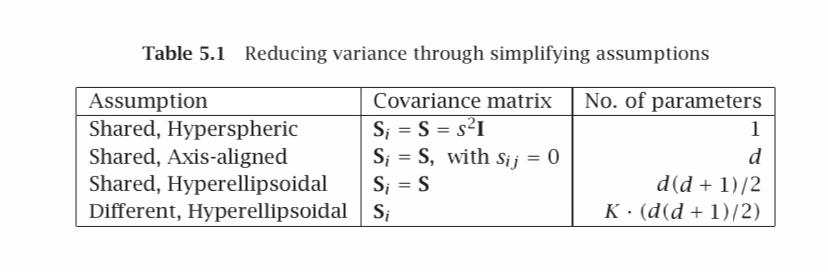
 

Table 5.1 Reducing variance through simplifying assumptions Assumption Covariance matrix No. of parameters S = S = s1 Shared, Hyperspheric Shared, Axis-aligned S = S, with Sij = 0 S = S Shared, Hyperellipsoidal Different, Hyperellipsoidal Si 1 d d(d + 1)/2 K (d(d+1)/2)