Purpose and Goal: We have discussed binary trees (BTs) and you will utilize them in a rough implementation of a famous compression algorithm: Huffman Compression. In this program you will utilize a pre-made Huffman compression tree to compress and decompress selected text strings.

Huffman Compression is a very useful compression algorithm that is utilized in several commonly used compression schemes. The details of Huffman compression, its viability and how the Huffman tree is initially created are not necessary for this project, but may be of interest to you. If you would like more information on the details of Huffman Compression, see: http://en.wikipedia.org/wiki/Huffman_coding

In this assignment, you must do the following:

1) Read in a representation of a Huffman tree from a text file and generate a Huffman tree of binary nodes. See more details below about the format of the file and requirements for the tree.

2) Use the tree generated in 1) above to create a Huffman encoding table. See more details below about the format of the encoding table.

3) Initiate an interactive session with the user that will continue until the user elects to quit. Each iteration has the following options:

a. Encode a word. In this case, show the user the set of valid characters and prompt the user to enter a word in normal text. Your program should output the equivalent Huffman codes as strings of 0's and 1's, with the code for each character being shown on a separate line. If the input String cannot be encoded properly, indicate this to the user. See example output in the files specified below.

b. Decode a Huffman code. In this case, show the user the Huffman encoding table and prompt the user to enter a Huffman string of 0s and 1s on a single line. There should be no spaces in the line. Your program should output the equivalent text string on a single line. If the Huffman code cannot be decoded properly, indicate this to the user. See example output in the files specified below.

c. Quit the program

Note that for a real Huffman code, the encoded output would be binary bits. Since we are instead using strings of 0's and 1's, we are not actually compressing anything (rather we are making the data bigger). However, we can still see how the process works and see what the binary bits WOULD be if we completed the implementation.

Reading the tree: Creating a Huffman tree from scratch is a non-trivial process. However, reading a representation of a Huffman tree from a file can be done in a fairly simple way utilizing recursion. The input file will consist of a number of lines of text. Each line will be one of two possibilities:

1) The single letter "I". This indicates that the node is an Interior node in the Huffman tree. For simplicity, in this case we will consider the root to also be an interior node. Due to the nature of Huffman trees, all interior nodes will have two children.

2) The single letter "L" followed by a single space, followed by a single letter. This indicates a Leaf node in the Huffman tree. The second letter on each line can be any upper-case letter, 'A' through 'Z', but each letter in the alphabet can appear in at most one line. These second letters represent the characters that can be encoded by the Huffman tree. For simplicity, assume that any subset of the alphabet in the file will always be a contiguous sequence starting at 'A'. For example, if the file contains only 5 letters, the leaf nodes will be 'A', 'B', 'C', 'D' and 'E'. However, they do not have to appear in the file in any particular order

Your algorithm can read the tree in the following way:

? Start with an empty binary tree, using the BinaryNode class from the text (or your extension of it) to store your tree nodes. Use BinaryNode for your node type so that you can store character values within your nodes.

? Recursively build the tree as follows:

- Read the next line from the file

- If the line starts with an "I", it represents an interior node and thus must have two children in the tree. Create a BinaryNode with a dummy character for its data (ex: '\0') and then recursively read in its left subtree and then recursively read in its right subtree.

- If the line starts with an "L", it represents a leaf node. Split the line and use the second character for the data value. Make a new BinaryNode using the data value. Note that this is a base case so it does not recurse.

See various example binary tree algorithms discussed in class for help with this process. Below is a simple example of the tree building algorithm:

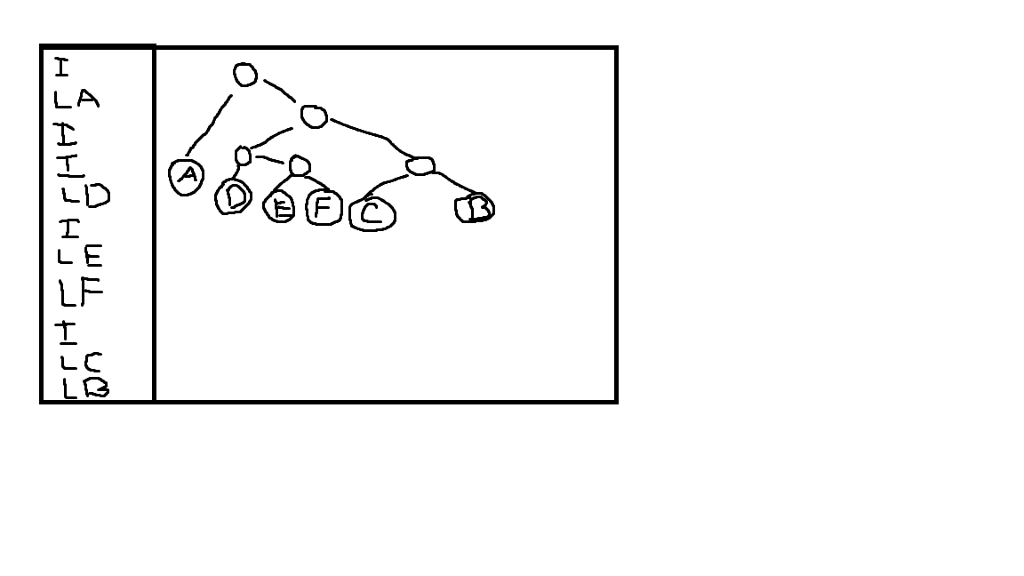
The file in the left box represents the Huffman tree shown in the right box. Even though the interior and leaf nodes look different in the picture, you will use the same type for all of your tree nodes.

To obtain actual Huffman codes from this tree, assign the value '0' to each left edge and the value '1' to each right edge. Thus, for example, the character 'D' would have the Huffman code "100" and the character 'F' would have the Huffman code "1011".

Creating the table: A Huffman tree can be used directly for decoding Huffman codes, but it is harder to use it for encoding. This is because to encode we need to start with a letter and end up with a Huffman code. However, in the Huffman tree the letters are leaves and we don't have an easy way of locating a particular letter, or of going back up the tree from a leaf. Thus, to encode we will first traverse the tree and generate an encoding table. This is actually fairly simple to do with an inorder traversal and a StringBuilder. As mentioned above, we will assign the bit '0' to the left child of a node and the bit '1' to the right child of a node. As we recursively traverse the tree, we add the correct bit to our StringBuilder with each recursive call, and we remove the bit when we backtrack. Upon reaching a leaf node, the current StringBuilder should contain the Huffman encoding string for that letter. We then store that value in an array of Strings. To make indexing easier, we will map the letter 'A' to location 0 and successive letters to the following locations. Given the example tree above, the resulting encoding table will be:

Index	Letter	Huffman Code
0	A	0
1	B	111
2	C	110
3	D	100
4	E	1010
5	F	1011

Encoding a text string: Once you have the encoding table built, encoding a string is a simple process. Simply iterate through the characters of the string. For each character, look up the Huffman code in the encoding table and append the results of all of the lookups together. To make it easier to grade, separate the codes of different letters with line feeds. For example, given the text string "BAD", your program would append "111", "0" and "100" to yield "111 0 100 ".

Decoding a Huffman string: Decoding a Huffman string works in the following way:

Start at the root of the Huffman tree and at the first bit (character) in the Huffman string

If the current bit is a '0', go left in the tree

If the current bit is a '1', go right in the tree

When a leaf in the tree is reached, append the corresponding character to the output and return to the root

Continue until all of the bits have been consumed

For example, given the Huffman code string: 1110100

The process would be:

Go right, go right, go right append 'B' and return to root

Go left append 'A' and return to root

Go right, go left, go left append 'D' and return to root

No more bits remain so the decoding is over return "BAD"

Representing the Tree: The Huffman tree must be stored as a dynamic tree of BinaryNodes. You may use the BinaryNode class as provided by the author (see the attached code), or you may modify it as necessary to make your implementation simpler. Either way, be sure to include all files that you use for this assignment, whether you have written them or the textbook author has written them.

To give you an idea of how the finished product would look, you can find some test runs. See the attached files a5out1.txt and a5out2.txt.

Extra CREDIT

As a challenging extra credit option, add code to generate the initial Huffman tree by processing a text file and creating the tree based on the relative frequencies of the characters in the file. Once the tree has been generated, save it in the format described above so that it can be read in again later if necessary. This is a lot of work so don't attempt it unless you have already completed the required elements of the assignment. You may need to consult various sources to see how the Huffman tree is initially generated.

PROVIDED CODE

BinaryNode.java /** * An implementation of the ADT Binary Node. * * This code is from * Chapter 24 of Data Structures and Abstractions with Java 4/e * by Carrano */ class BinaryNode {

private T data; private BinaryNode leftChild; private BinaryNode rightChild;

public BinaryNode() { this(null); // Call next constructor } // end default constructor

public BinaryNode(T dataPortion) { this(dataPortion, null, null); // Call next constructor } // end constructor

public BinaryNode(T dataPortion, BinaryNode newLeftChild, BinaryNode newRightChild) { data = dataPortion; leftChild = newLeftChild; rightChild = newRightChild; } // end constructor

/** * Retrieves the data portion of this node. * * @return The object in the data portion of the node. */ public T getData() { return data; } // end getData

/** * Sets the data portion of this node. * * @param newData The data object. */ public void setData(T newData) { data = newData; } // end setData

/** * Retrieves the left child of this node. * * @return The node that is this node's left child. */ public BinaryNode getLeftChild() { return leftChild; } // end getLeftChild

/** * Sets this node's left child to a given node. * * @param newLeftChild A node that will be the left child. */ public void setLeftChild(BinaryNode newLeftChild) { leftChild = newLeftChild; } // end setLeftChild

/** * Detects whether this node has a left child. * * @return True if the node has a left child. */ public boolean hasLeftChild() { return leftChild != null; } // end hasLeftChild

/** * Retrieves the right child of this node. * * @return The node that is this node's right child. */ public BinaryNode getRightChild() { return rightChild; } // end getRightChild

/** * Sets this nodes's right child to a given node. * * @param newRightChild A node that will be the right child. */ public void setRightChild(BinaryNode newRightChild) { rightChild = newRightChild; } // end setRightChild

/** * Detects whether this node has a right child. * * @return True if the node has a right child. */ public boolean hasRightChild() { return rightChild != null; } // end hasRightChild

/** * Detects whether this node is a leaf. * * @return True if the node is a leaf. */ public boolean isLeaf() { return (leftChild == null) && (rightChild == null); } // end isLeaf

/** * Computes the height of the subtree rooted at this node. * * @return The height of the subtree rooted at this node. */ public int getHeight() { return getHeight(this); // Call private getHeight } // end getHeight

private int getHeight(BinaryNode node) { int height = 0; if (node != null) { height = 1 + Math.max(getHeight(node.getLeftChild()), getHeight(node.getRightChild())); } return height; } // end getHeight

/** * Counts the nodes in the subtree rooted at this node. * * @return The number of nodes in the subtree rooted at this node. */ public int getNumberOfNodes() { int leftNumber = 0; int rightNumber = 0;

if (leftChild != null) { leftNumber = leftChild.getNumberOfNodes(); }

if (rightChild != null) { rightNumber = rightChild.getNumberOfNodes(); }

return 1 + leftNumber + rightNumber; } // end getNumberOfNodes

/** * Copies the subtree rooted at this node. * * @return The root of a copy of the subtree rooted at this node. */ public BinaryNode copy() { BinaryNode newRoot = new BinaryNode(data); if (leftChild != null) { newRoot.setLeftChild(leftChild.copy()); } if (rightChild != null) { newRoot.setRightChild(rightChild.copy()); } return newRoot; } // end copy

} // end BinaryNode

a5out1.txt

> java Assig5 huff1.txt

The Huffman Tree has been restored

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 1 Enter a String from the following characters: ABCDEF BAD Huffman String: 111 0 100

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 0 B: 111 C: 110 D: 100 E: 1010 F: 1011 Please enter a Huffman string (one line, no spaces) 1110100 Text string: BAD

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 1 Enter a String from the following characters: ABCDEF CAFE Huffman String: 110 0 1011 1010

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 0 B: 111 C: 110 D: 100 E: 1010 F: 1011 Please enter a Huffman string (one line, no spaces) 110010111010 Text string: CAFE

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 1 Enter a String from the following characters: ABCDEF Q There was an error in your text string

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 0 B: 111 C: 110 D: 100 E: 1010 F: 1011 Please enter a Huffman string (one line, no spaces) 01 There was an error in your Huffman string

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 3 Good-bye

a5out2.txt

> java Assig5 huff2.txt

The Huffman Tree has been restored

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 1 Enter a String from the following characters: ABCDEFGHI FADED Huffman String: 011010 00 01011 01100 01011

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 00 B: 0100 C: 01010 D: 01011 E: 01100 F: 011010 G: 011011 H: 0111 I: 1 Please enter a Huffman string (one line, no spaces) 01101000010110110001011 Text string: FADED

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 1 Enter a String from the following characters: ABCDEFGHI ICE Huffman String: 1 01010 01100

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 00 B: 0100 C: 01010 D: 01011 E: 01100 F: 011010 G: 011011 H: 0111 I: 1 Please enter a Huffman string (one line, no spaces) 10101001100 Text string: ICE

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 2 Here is the encoding table: A: 00 B: 0100 C: 01010 D: 01011 E: 01100 F: 011010 G: 011011 H: 0111 I: 1 Please enter a Huffman string (one line, no spaces) 011011000100 Text string: GAB

Please choose from the following: 1) Encode a text string 2) Decode a Huffman string 3) Quit 3 Good-bye

huff1.txt

I L A I I L D I L E L F I L C L B

huff2.txt

I I L A I I L B I L C L D I I L E I L F L G L H L I

LA LD L E LF TI LC LO