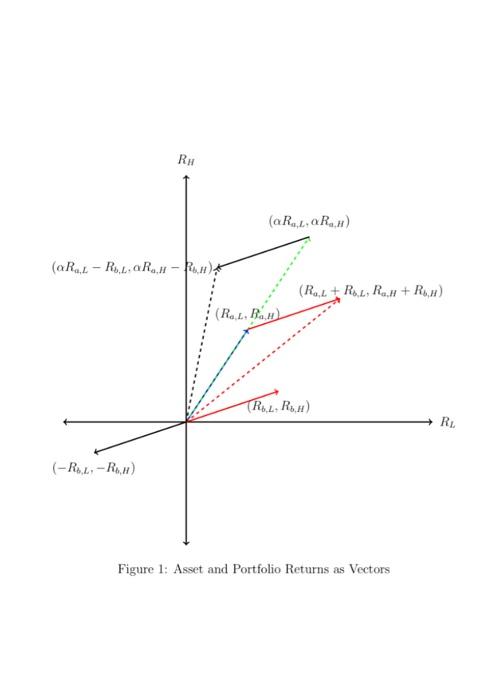
PURPOSE: In this problem set, you are to draw asset portfolio returns to highlight the concept of complete vs incomplete asset return structures. This is meant to illustrate an individual's ability to use asset portfolios to achieved desired returns across different states-of-nature. It is directly related to our discussion about the ability of an individual to completely insure their consumption risk or only partially insure their consumption risk Consider an individual facing the prospect of having high income, ya > 0, with probability and low income, y: with probability 1 - TY > y. Prior to learning whether realized income is high or low, the individual is able to go into the market and purchase (or sell) two types of assets. Let the Asset 1 have a return structure such that it pays R units of goods if y = y and pays R1,2 units of goods if y = yL. Similarly, let Asset 2 have a return structure such that it pays R24 units of goods if y = yn and pays R2,4 units of goods if y = y. The individual is endowed with w units of wealth to spend in the asset market but this wealth is not storable and hence cannot be save to purchase consumption goods. Denote by a, the amount of Asset 1 purchased by the individual and as the amount of Asset 2 purchased by the individual. Definition 1 An asset's return structure is state-contingent if the realized return of the asset varies across states-of-nature. If an asset pays yields the same return across states-of-nature, then it has a return structure that is non-contingent. In our exercise, as the the structure of return for asset i is ( RR) and depends on the individual's income (which is the realized state-of-nature) then if RL #RH then the asset's return structure is state-contingent (the return depends on the realized state-of-nature) The individual's problem is to maximize the expected utility from consumption sub- ject to the constraints that consumption must be financed out of income and the realized return from the asset portfolio as well as a constraint that spending on the asset portfolio must be financed out of the non-storable endowment wealth w. Consumption and portfolio spending satisfies the following constraints, = y + R/+R2.Ha2 + (1) = yL+ R... + R2,202 (2) w = a1 + 02. (3) Note that a and a, can be positive (purchase) or negative (sell). Definition 2 An asset structure is complete from the perspective of an economic actor if the actor is, in effect, unrestricted (up to their budget constraints) in the ability to transfer wealth across states-of-nature. CH CL One way to think about this is that if there are N states-of-nature, then a complete asset structure allows the individual the flexibility to construct combinations of payoffs that can vary in N different directions. If the asset structure is incomplete then the individual can only choose from payoffs that vary in MN directions. Note that in referring to the asset structure, we are referring to the possibility of constructing portfolio returns to acheive any combination of portfolio returns across the N states-of-nature using all the available assets; we are not referring to the asset return structure of a single asset. 1. Suppose that R1 = a R2., and R12 = R2, L. Then if a 0, with probability and low income, y: with probability 1 - TY > y. Prior to learning whether realized income is high or low, the individual is able to go into the market and purchase (or sell) two types of assets. Let the Asset 1 have a return structure such that it pays R units of goods if y = y and pays R1,2 units of goods if y = yL. Similarly, let Asset 2 have a return structure such that it pays R24 units of goods if y = yn and pays R2,4 units of goods if y = y. The individual is endowed with w units of wealth to spend in the asset market but this wealth is not storable and hence cannot be save to purchase consumption goods. Denote by a, the amount of Asset 1 purchased by the individual and as the amount of Asset 2 purchased by the individual. Definition 1 An asset's return structure is state-contingent if the realized return of the asset varies across states-of-nature. If an asset pays yields the same return across states-of-nature, then it has a return structure that is non-contingent. In our exercise, as the the structure of return for asset i is ( RR) and depends on the individual's income (which is the realized state-of-nature) then if RL #RH then the asset's return structure is state-contingent (the return depends on the realized state-of-nature) The individual's problem is to maximize the expected utility from consumption sub- ject to the constraints that consumption must be financed out of income and the realized return from the asset portfolio as well as a constraint that spending on the asset portfolio must be financed out of the non-storable endowment wealth w. Consumption and portfolio spending satisfies the following constraints, = y + R/+R2.Ha2 + (1) = yL+ R... + R2,202 (2) w = a1 + 02. (3) Note that a and a, can be positive (purchase) or negative (sell). Definition 2 An asset structure is complete from the perspective of an economic actor if the actor is, in effect, unrestricted (up to their budget constraints) in the ability to transfer wealth across states-of-nature. CH CL One way to think about this is that if there are N states-of-nature, then a complete asset structure allows the individual the flexibility to construct combinations of payoffs that can vary in N different directions. If the asset structure is incomplete then the individual can only choose from payoffs that vary in MN directions. Note that in referring to the asset structure, we are referring to the possibility of constructing portfolio returns to acheive any combination of portfolio returns across the N states-of-nature using all the available assets; we are not referring to the asset return structure of a single asset. 1. Suppose that R1 = a R2., and R12 = R2, L. Then if a