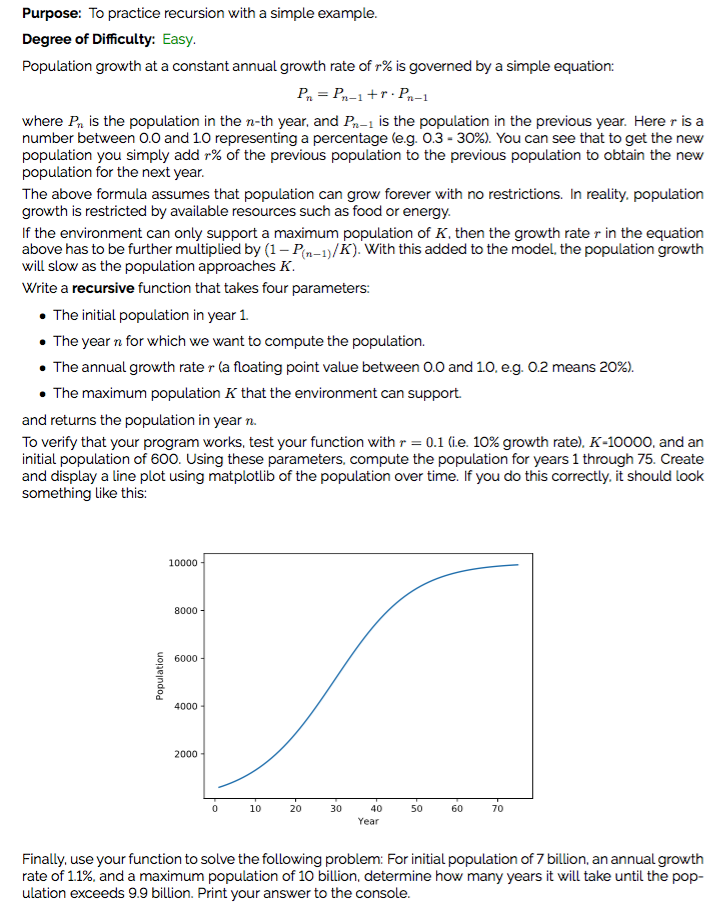
Purpose: To practice recursion with a simple example Degree of Difficulty: Easy Population growth at a constant annual growth rate of 1% is governed by a simple equation: where P is the population in the n-th year, and P- is the population in the previous year. Here r is a number between O.O and 10 representing a percentage (eg, 03-30%). You can see that to get the new population you simply add 1% of the previous population to the previous population to obtain the new population for the next year The above formula assumes that population can grow forever with no restrictions. In reality. population growth is restricted by available resources such as food or energy. If the environment can only support a maximum population of K, then the growth rate r in the equation above has to be further multiplied by (1 - Pn-1)/K). With this added to the model, the population growth will slow as the population approaches K Write a recursive function that takes four parameters: . The initial population in year 1 . The year n for which we want to compute the population. . The annual growth rate r (a floating point value between O.O and 10, e.g. 02 means 20%). . The maximum population K that the environment can support. and returns the population in year n. To verify that your program works, test your function with r-0.1 (ie. 10% growth rate), K-10000, and an initial population of 600. Using these parameters, compute the population for years 1 through 75. Create and display a line plot using matplotlib of the population over time. If you do this correctly. it should look something like this: 10000 8000 6000 4000 2000 10 20 30 40 Year 50 60 70 Finally, use your function to solve the following problem: For initial population of 7 billion, an annual growth rate of 11%, and a maximum population of 10 billion, determine how many years it will take until the pop- ulation exceeds 9.9 billion. Print your answer to the console Purpose: To practice recursion with a simple example Degree of Difficulty: Easy Population growth at a constant annual growth rate of 1% is governed by a simple equation: where P is the population in the n-th year, and P- is the population in the previous year. Here r is a number between O.O and 10 representing a percentage (eg, 03-30%). You can see that to get the new population you simply add 1% of the previous population to the previous population to obtain the new population for the next year The above formula assumes that population can grow forever with no restrictions. In reality. population growth is restricted by available resources such as food or energy. If the environment can only support a maximum population of K, then the growth rate r in the equation above has to be further multiplied by (1 - Pn-1)/K). With this added to the model, the population growth will slow as the population approaches K Write a recursive function that takes four parameters: . The initial population in year 1 . The year n for which we want to compute the population. . The annual growth rate r (a floating point value between O.O and 10, e.g. 02 means 20%). . The maximum population K that the environment can support. and returns the population in year n. To verify that your program works, test your function with r-0.1 (ie. 10% growth rate), K-10000, and an initial population of 600. Using these parameters, compute the population for years 1 through 75. Create and display a line plot using matplotlib of the population over time. If you do this correctly. it should look something like this: 10000 8000 6000 4000 2000 10 20 30 40 Year 50 60 70 Finally, use your function to solve the following problem: For initial population of 7 billion, an annual growth rate of 11%, and a maximum population of 10 billion, determine how many years it will take until the pop- ulation exceeds 9.9 billion. Print your answer to the console







