PY CH6 HW4:

1)

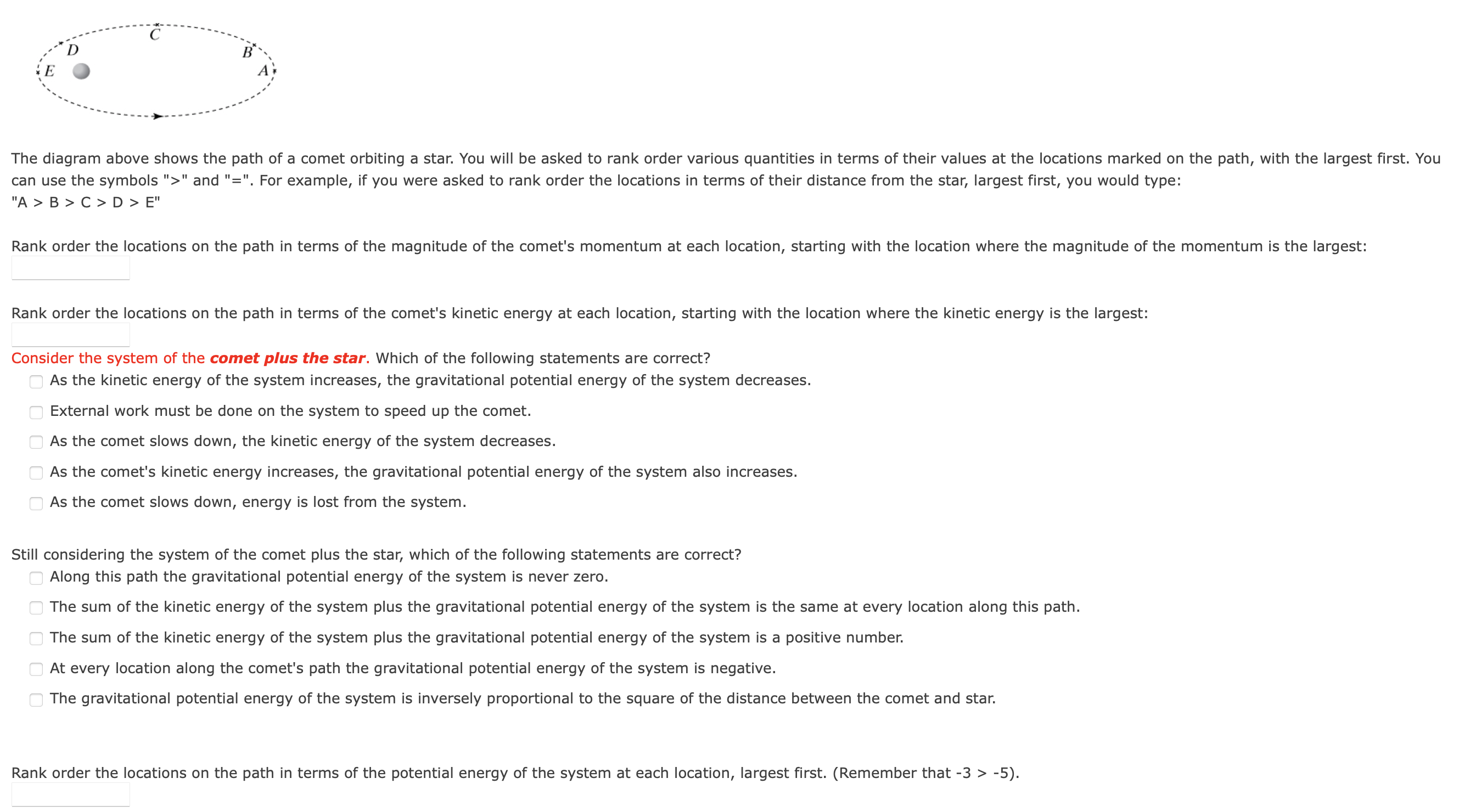
Consider an isolated system, by which we mean a system free of external forces. If the sum of the particle energies in the system increases by 154 joules, what must have been the change AU in the system's potential energy? AU = J The diagram above shows the path of a comet orbiting a star. You will be asked to rank order various quantities in terms of their values at the locations marked on the path, with the largest first. You can use the symbols \">" and "=". For example, if you were asked to rank order the locations in terms of their distance from the star, largest first, you would type: "A>B>C>D>E" Rank order the locations on the path in terms of the magnitude of the comet's momentum at each location, starting with the location where the magnitude of the momentum is the largest: Rank order the locations on the path in terms of the comet's kinetic energy at each location, starting with the location where the kinetic energy is the largest: Consider the system of the comet plus the star. Which of the following statements are correct? As the kinetic energy of the system increases, the gravitational potential energy of the system decreases. External work must be done on the system to speed up the comet. As the comet slows down, the kinetic energy of the system decreases. As the comet's kinetic energy increases, the gravitational potential energy of the system also increases. As the comet slows down, energy is lost from the system. Still considering the system of the comet plus the star, which of the following statements are correct? Along this path the gravitational potential energy of the system is never zero. The sum of the kinetic energy of the system plus the gravitational potential energy of the system is the same at every location along this path. The sum of the kinetic energy of the system plus the gravitational potential energy of the system is a positive number. At every location along the comet's path the gravitational potential energy of the system is negative. The gravitational potential energy of the system is inversely proportional to the square of the distance between the comet and star. Rank order the locations on the path in terms of the potential energy of the system at each location, largest rst. (Remember that ~3 > -5). A comet is in an elliptical orbit around the Sun. Its closest approach to the Sun is a distance of 4.7 x 1010 m (inside the orbit of Mercury), at which point its speed is 9.1 x 104 m/s. Its farthest distance from the Sun is far beyond the orbit of Pluto. What is its speed when it is 6 X 1012 m from the Sun? (This is the approximate distance of Pluto from the Sun.) speed = m/s The radius of Jupiter (from the center to just above the atmosphere) is 71500 km (71500x103 m), and its mass is 1900x1024 kg. An object is launched straight up from just above the atmosphere of Jupiter. (a) What initial speed is needed so that when the object is far from Jupiter its final speed is 47500 m/s? Vinitial = "1/5 (b) What initial speed is needed so that when the object is far from Jupiter its final speed is 0 m/s? (This is called the "escape speed.") Vescape = m/S In certain cases, using both the momentum principle and energy principle to analyze a system is useful, as they each can reveal different information. You will use the both momentum principle and the energy principle in this problem. A satellite of mass 2500 kg orbits the Earth in a circular orbit of radius of 8.8 x 106 m (this is above the Earth's atmosphere).The mass of the Earth is 6.0 x 1024 kg. What is the magnitude of the gravitational force on the satellite due to the earth? F = N Using the momentum principle, find the speed of the satellite in orbit. (HINT: Think about the components of (IF/'1' parallel and perpendicular to 17.) v = m/s Using the energy principle, nd the minimum amount of work needed to move the satellite from this orbit to a location very far away from the Earth. (You can think of this energy as being supplied by work due to something outside of the system of the Earth and the satellite.) work = J The diagram below is a graph of the energy of a system of a planet interacting with a star. The gravitational potential energy U9 is shown as the thick curve, and plotted along the vertical axis are various values of K+Ug. "1 '2 r, from star to planet Suppose that K+Ug of the system is A. Which of the following statements are true? when the separation between the two bodies is r2, the kinetic energy of the system is (A B). The potential energy of the system decreases as the planet moves from r1 to r2. When the separation between the two bodies is r2, the kinetic energy of the system is (B - C). The kinetic energy of the system is greater when the distance between the star and planet is r1 than when the distance between the two bodies is r2. The planet will escape. The system is a bound system; the planet can never escape. Suppose instead that K+Ug of the system is B. Which of the following statements are true? when the separation between the planet and star is r2, the potential energy of the system is zero. When the separation between the planet and star is r2, the kinetic energy of the system is zero. This is not a bound system; the planet can escape. The planet and star cannot get farther apart than r2. The escape speed from a very small asteroid is only 20 m/s. If you throw a rock away from the asteroid at a speed of 28 m/s, what will be its final speed? vf = m/s You stand on a spherical asteroid of uniform density whose mass is 2,5x1o16 kg and whose radius is 11 km (11x103 m). These are typical values for small asteroids, although some asteroids have been found to have much lower average density and are thought to be loose agglomerations of shattered rocks. You want to figure out how fast you have to throw the rock so that it never comes back to the asteroid and ends up traveling at a speed of 10 m/s when it is very far away, What fundamental principle(s) will you use in your solution? No fundamental principles are applicable The Energy Principle The Momentum Principle what are useful choices for the initial and nal states of the system? In the nal state the rock is very far away moving at 10 m/s In the nal state the rock has just le your hand in the final state the rock is very far away, at rest In the initial state the rock is at rest in your hand In the initial state the rock has just left your hand in the initial state the rock is in your hand, which is moving Which of these quantities are important in your solution7 The initial potential energy of the rock+asteroid system The nal kinetic energy of the rock The rest energy MC 2 of the rock The time it takes for the rock to get far away The rest energy Mammy: 2 of the asteroid The force exerted by your hand on the rock The initial kinetic energy of the rock The nal potential energy of the rock+asteroid system which of the following are true in this problem? The nal kinetic energy of the rock is less than its initial kinetic energy The nal potential energy of the roek+asteroid system is less than the initial potential energy of the system The nal kinetic energy of the rock is u The total energy of the rock+asteroid system is less in the nal state than in the initial state The change in the kinetic energy of the asteroid is negligible How fast do you have to throw the rock so that it never comes back to the asteroid and ends up traveling at a speed of1o m/s when it is very far away? launch speed (relative to you) : rn/s Which graph best describes the kinetic and potential energy of the rock+asterold system as a function of distance between the rock and the asteroid? A a c o to \\f' y W ii if a't You will need to use the Momentum Principle to do the rst part of this problem, and the Energy Principle to do the second part. A satellite of mass 3500 kg orbits the Earth in a circular orbit of radius of 3.4 x 106 in (this is above the Earth's atmosphere).The mass of the Earth is 6.0 x 1024 kg. What is the speed of the satellite? v = m/s What is the minimum amount of energy required to move the satellite from this orbit to a location very far away from the Earth? energy = J