Python coding

Q3(a) (4 marks)

A fictional forest trail starts from a given point START. At the start or at further named points the path can fork into a left path and a right path. At any point there can be a left path only or a right path only. The trail can be represented by a rooted binary tree, such as:

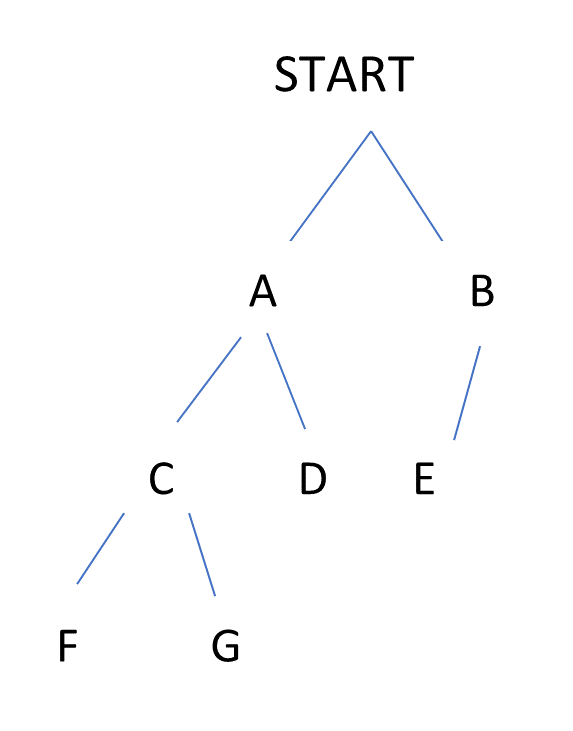
For this example, the trail ends at the leaves of the tree, that is, D, E, F and G.

Given a trail represented by a rooted tree, trail, write a recursive function called ends that calculates the number of points at which a trail ends. For the example above, this would return 4.

Test your function by running the test code given below. If any tests fail, then debug your function, and run the test code again. You can repeat this iterative process as many times as you want. If there are any tests that fail and you are unable to identify the problem, you may add explanatory comments below the test code.

The file m269_util.py contains the code for the test function.

%run -i m269_tree %run -i m269_util # Compute the number of trail ends in trail # Write your recursive function here

# Test code EMPTY = Tree() F = join('F',EMPTY,EMPTY) G = join('G',EMPTY,EMPTY) C = join('C',F,G) D = join('D', EMPTY,EMPTY) A = join('A',C,D) E = join('E',EMPTY,EMPTY) B = join('B',E,EMPTY) START = join('START',A,B)

trail_tests = [ # case, trail, number of trail ends ('empty tree', EMPTY, 0), ('no subtrees, already trail end', F, 1), ('one subtree, trail end', B, 1), ('two subtrees, neither subtree is a trail end', START, 4), ('two subtrees, one subtree is a trail end', A, 3), ('two subtrees, both subtrees are trail ends', C, 2) ] test(ends, trail_tests) # Add any explanatory comments here

Q3(b) (8 marks)

Here is a definition of a function is BST that takes a binary tree and decides if it is a binary search tree.

Function: is BST Inputs: t, a binary tree Preconditions: items in the t must be (pairwise) comparable Output: result, a Boolean Postconditions: result is true if t is a binary search tree, or if for every node in t the left child is either empty or less than the node's root and the right child is either empty or greater than the node's root - and false otherwise

The recursive function is_BST() provided in the file Q3_BST.py implements the is BST function.

Write code to construct test trees and complete the test table with six different tests to test this implementation. Add comments to the test table to indicate any edge cases.

Running the test code should produce 'Tests finished'. If any tests fail, try to identify why they failed and add any explanatory comments below the test code.

%run -i m269_tree %run -i m269_util %run -i Q3_BST

# Write your code to construct test trees here

# Complete the test table BST_tests = [ # case, t, result # Add your tests here, uncomment the tests when you are ready to use them # ('', , ), # ('', , ), # ('', , ), # ('', , ), # ('', , ), # ('', , ) ]

test(is_BST, BST_tests)

# Add any explanatory comments here

Question 4 (38 marks)

You should be able to answer this question after you have studied Chapters 16, 17 and 18.

This question tests the following learning outcomes:

Apply general-purpose data structures and algorithmic techniques to efficiently solve computational problems.

Explain in a clear and succinct way how an algorithm or data structure works, and its assumptions, in order to communicate with peers.

Analyse the complexity of algorithms to support design choices.

Write readable, tested and documented Python functions and classes to implement algorithms and abstract data types.

The files m269_digraph.py, m269_ungraph.py and Q4_warehouse.py should be in the folder with this

A warehouse, similar to Ocados algorithm-controlled warehouse that you met in The Secret Rules of Modern Living: Algorithms Part 3, has a despatch area and a vast storage area divided into zones. Requested items are brought to despatch from the storage area by an automatic picking system. An automated crate travels along tracks from despatch to the appropriate storage area zones, and back to despatch. Tracks are in pairs that allow the crate to travel in either direction.

The crate may need to pass through other zones to get to and from the zones where the requested items are.

The warehouse can be represented by a weighted digraph. Nodes represent the despatch and storage zones. Weighted edges represent tracks between the despatch and storage zones, and between zones. A weight represents the time (in seconds) that it takes to travel between the two zones joined by the edge.

Run the code below to draw an instance of a weighted digraph that represents an example warehouse.

%run -i m269_digraph %run -i m269_ungraph from matplotlib.pyplot import * %run -i Q4_warehouse

START