Python coding question

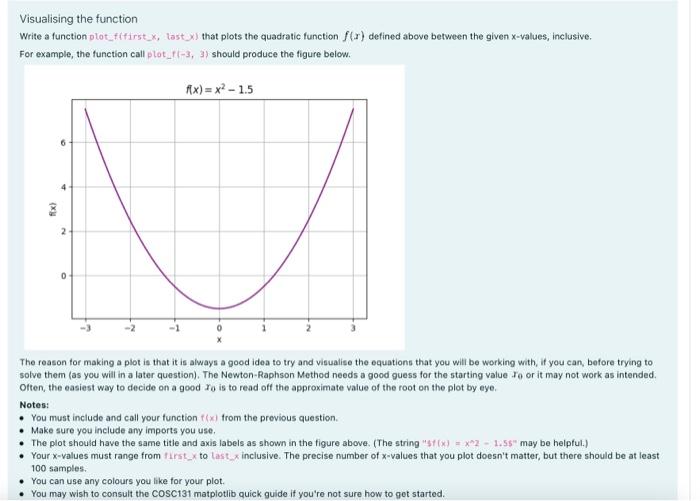
a The Newton-Raphson Method Be sure to watch the video introducing the Newton-Raphson method before proceeding We begin our exploration of numerical methods with a cool algorithm for finding the roots (zeros) of a function: the Newton-Raphson method, sometimes simply called Newton's method. Between 1665 and 1666, Isaac Newton (1642 - 1727) spent his days under lockdown in his countryside home at Woolsthorpe, England while the Great Plague was ravaging London. During these so-called "plague years" Newton was free to think, observe, and create. His many discoveries from this productive period of his life include the development of calculus, the laws of classical mechanics, the theory of gravitation, and the workings of optics. Among these massive achievements was a little algorithmic gem that we will now discuss. The algorithm The algorithm in question - which later became known simply as "Newton's Method" or the "Newton-Raphson Method" after Joseph Raphson (c. 1648 - c. 1715) who elaborated on the algorithm - could be used to find the roots of an arbitrary function. Finding a root of a function f() just means finding a value of such that t) = 0. Newton's method involves computing a series of increasing accurate estimates of the root as follows: 1. Choose an initial value for the root, 7, and call it to 2. Compute an improved estimate x142 11 - where f[?[?][?](x) is the derivative of f(x). 3. Go back to step 2 The above generates an intinite sequence of t; In practice we stop as soon as we have a sufficiently good" estimate of the actual root, as will be explained in the information panels and questions that follow. Visualising the function Write a function plot_fifirst_x, last x) that plots the quadratic function f(x) defined above between the given x-values, inclusive. For example, the function call plot_-3, 3) should produce the figure below. fx) = x2 - 1.5 2 0 The reason for making a plot is that it is always a good idea to try and visualise the equations that you will be working with, if you can, before trying to solve them (as you will in a later question). The Newton-Raphson Method needs a good guess for the starting value to or it may not work as intended, Often, the easiest way to decide on a good to is to read off the approximate value of the root on the plot by eye. Notes: You must include and call your function(x) from the previous question. . Make sure you include any imports you use. The plot should have the same title and axis labels as shown in the figure above. (The string "700) = x^2 - 1.55" may be helpful.) Your x-values must range from first to last inclusive. The precise number of x-values that you plot doesn't matter, but there should be at least 100 samples. You can use any colours you like for your plot. . You may wish to consult the COSC131 matplotlib quick guide if you're not sure how to get started