

 python please
python please
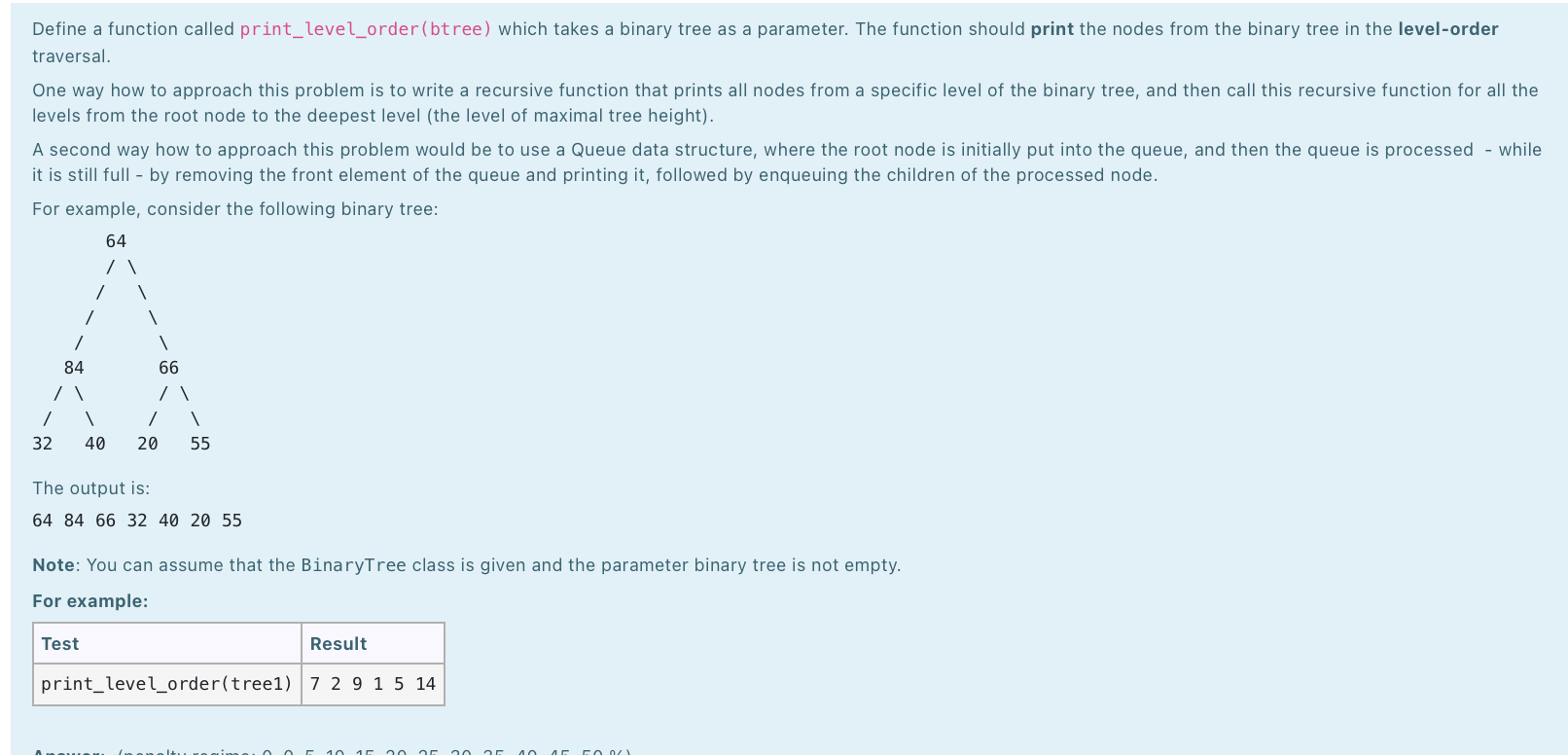
The purpose of this laboratory is for you to demonstrate your understanding of Binary Trees. The BinaryTree class definition is given as follows: class BinaryTree: def __init__(self, data, left=None, right=None): self.__data = data self._left = left self.__right = right def insert_left(self, new_data): if self._left == None: self._left = BinaryTree (new_data) else: tree = BinaryTree (new_data, left=self. __left) self._left = tree def insert_right (self, new_data): if self._right == None: self._right = BinaryTree(new_data) else: tree = BinaryTree (new_data, right=self.__right) self.__right = tree def get_left(self): return self._left def get_right (self): return self._right def set_data(self, data): self. __data = data def get_data(self): return self.__data def set_left(self, left): self._left = left def set_right(self, right): self._right = right IMPORTANT: For these exercises, you will be defining a function which USES the BinaryTree ADT. A BinaryTree implementation is provided to you as part of this exercise - you should not define your own BinaryTree class. Instead, your code can make use of any of the BinaryTree ADT methods: BinaryTree(), get_data(), set_data(), get_left(), set_left(), get_right(), set_right(), insert_left() and insert_right(). Consider the following nested list: [95, [74, [52, None, None], [1, None, None]], [100, [14, None, None], [97, None, None]]] The nested list format always uses a list of length three to represent a binary tree. The first item in the list is the data value of the root, the second item in the list is the left subtree (this may be None if the left subtree is empty, or it may be a nested list) and the third item in the list is the right subtree (this may be None if the right subtree is empty, or it may be a nested list). Define a function called create_sample_tree () which builds and returns the above binary tree: Note: you can assume that the BinaryTree class and the print_tree() function are given. For example: Test Result 74 b_tree = create_sample_tree() 95 print_tree (b_tree, 0) (L) (L) (R) (R) (L) (R) 52 1 100 14 97 Define a function called print_level_order(btree) which takes a binary tree as a parameter. The function should print the nodes from the binary tree in the level-order traversal. One way how to approach this problem is to write a recursive function that prints all nodes from a specific level of the binary tree, and then call this recursive function for all the levels from the root node to the deepest level (the level of maximal tree height). A second way how to approach this problem would be to use a Queue data structure, where the root node is initially put into the queue, and then the queue is processed - while it is still full - by removing the front element of the queue and printing it, followed by enqueuing the children of the processed node. For example, consider the following binary tree: 64 / / / 66 84 / / 32 40 / / 20 55 The output is: 64 84 66 32 40 20 55 Note: You can assume that the BinaryTree class is given and the parameter binary tree is not empty. For example: Test Result print_level_order(tree1) 7 2 9 1 5 14 F The purpose of this laboratory is for you to demonstrate your understanding of Binary Trees. The BinaryTree class definition is given as follows: class BinaryTree: def __init__(self, data, left=None, right=None): self.__data = data self._left = left self.__right = right def insert_left(self, new_data): if self._left == None: self._left = BinaryTree (new_data) else: tree = BinaryTree (new_data, left=self. __left) self._left = tree def insert_right (self, new_data): if self._right == None: self._right = BinaryTree(new_data) else: tree = BinaryTree (new_data, right=self.__right) self.__right = tree def get_left(self): return self._left def get_right (self): return self._right def set_data(self, data): self. __data = data def get_data(self): return self.__data def set_left(self, left): self._left = left def set_right(self, right): self._right = right IMPORTANT: For these exercises, you will be defining a function which USES the BinaryTree ADT. A BinaryTree implementation is provided to you as part of this exercise - you should not define your own BinaryTree class. Instead, your code can make use of any of the BinaryTree ADT methods: BinaryTree(), get_data(), set_data(), get_left(), set_left(), get_right(), set_right(), insert_left() and insert_right(). Consider the following nested list: [95, [74, [52, None, None], [1, None, None]], [100, [14, None, None], [97, None, None]]] The nested list format always uses a list of length three to represent a binary tree. The first item in the list is the data value of the root, the second item in the list is the left subtree (this may be None if the left subtree is empty, or it may be a nested list) and the third item in the list is the right subtree (this may be None if the right subtree is empty, or it may be a nested list). Define a function called create_sample_tree () which builds and returns the above binary tree: Note: you can assume that the BinaryTree class and the print_tree() function are given. For example: Test Result 74 b_tree = create_sample_tree() 95 print_tree (b_tree, 0) (L) (L) (R) (R) (L) (R) 52 1 100 14 97 Define a function called print_level_order(btree) which takes a binary tree as a parameter. The function should print the nodes from the binary tree in the level-order traversal. One way how to approach this problem is to write a recursive function that prints all nodes from a specific level of the binary tree, and then call this recursive function for all the levels from the root node to the deepest level (the level of maximal tree height). A second way how to approach this problem would be to use a Queue data structure, where the root node is initially put into the queue, and then the queue is processed - while it is still full - by removing the front element of the queue and printing it, followed by enqueuing the children of the processed node. For example, consider the following binary tree: 64 / / / 66 84 / / 32 40 / / 20 55 The output is: 64 84 66 32 40 20 55 Note: You can assume that the BinaryTree class is given and the parameter binary tree is not empty. For example: Test Result print_level_order(tree1) 7 2 9 1 5 14 F


 python please
python please





