Python Problem

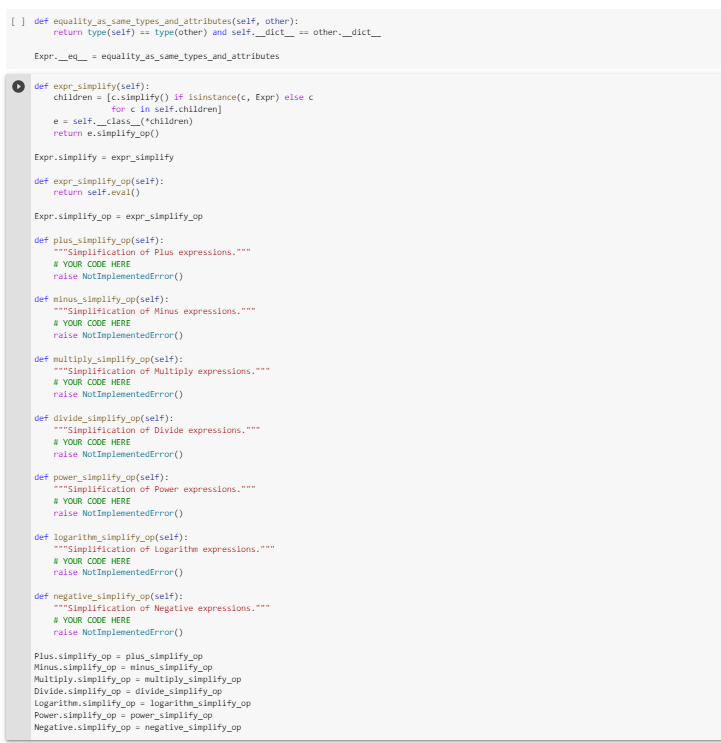
def expr_simplify(self):

children = [c.simplify() if isinstance(c, Expr) else c

for c in self.children]

e = self.__class__(*children)

return e.simplify_op()

Expr.simplify = expr_simplify

def expr_simplify_op(self):

return self.eval()

Expr.simplify_op = expr_simplify_op

def plus_simplify_op(self):

"""Simplification of Plus expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def minus_simplify_op(self):

"""Simplification of Minus expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def multiply_simplify_op(self):

"""Simplification of Multiply expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def divide_simplify_op(self):

"""Simplification of Divide expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def power_simplify_op(self):

"""Simplification of Power expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def logarithm_simplify_op(self):

"""Simplification of Logarithm expressions."""

# YOUR CODE HERE

raise NotImplementedError()

def negative_simplify_op(self):

"""Simplification of Negative expressions."""

# YOUR CODE HERE

raise NotImplementedError()

Plus.simplify_op = plus_simplify_op

Minus.simplify_op = minus_simplify_op

Multiply.simplify_op = multiply_simplify_op

Divide.simplify_op = divide_simplify_op

Logarithm.simplify_op = logarithm_simplify_op

Power.simplify_op = power_simplify_op

Negative.simplify_op = negative_simplify_op

Problem 3: Expression simplification Although we can take the derivatives of various expressions, the results might not be exactly what we were hoping for. For example, the derivative of 5y +1 with respect to y should be 5, but it comes out as Plus (Plus (Multiply(e, V'y'), 5), ). This is equivalent to 5 (because 0 x y=0,0+5 = 5, and 5 +0=5), but it is rather ugly to read: [] e = 5 * Vy') + 1 e.derivative('y') Although calling eval() would help in many cases, in this situation calling eval() on e.derivative('y') would not help, because we do not have a value for the variable (y'). But what we can do instead is implement a method to simplify expressions like this one. For this problem, you will write methods implementing simplification of expressions for each subclass of Expr. You should implement the following simplifications: Plus(@, e) and Plus(e, ) should simplify to e, for any e. Minus(e, o) should simplify to e, for any e. Minus(@, e) should simplify to Negative(e). Multiply(@, e) and Multiply(e, a) should simplify to e, for any e. Multiply(1, e) and Multiply(e, 1) should simplify to e, for any e. Divide (@, e) should simplify to e, for any e. Divide(e, 1) should simplify to e, for any e Power(1, e) should simplify to 1, for any e. Power(e, ) should simplify to 1, for any e. Power(e, 1) should simplify to e, for any e. Logarithm(1) should simplify to e. Negative() should simplify to e. The simplification rules should be applied recursively over the expression, so that v('x') *(1 + ('') * %) should be simplifed to v('x'). To get you started, we have implemented a simplify method for the Expr class, which relies on each subclass having implemented a simplify_op method. Your task is to implement these simplify_op methods for the Plus, Minus, Multiply, Divide, Logarithm, Power, and Negative classes. The methods you write should implement the simplifications described above for each expression type, and return a simplified expression. If none of the above simplifications are possible, each simplify op method should call eval() on the expression. Finally, in order to test your simplify_op implementations, we need to be able to check for expression equality, with a more lenient notion of equality than Python's "same object" notion. The below cell should do the job; be sure to run it before you test your code. I def equality_as_same_types_and_attributes(self, other): return type(self) == type(other) and self._dict__ == other. _dict__ Expr. _e__ = equality_as_same_types_and_attributes def expr_simplify(self): children = [c.simplify() if isinstance(C, Expr) else C for c in self.children] e = self._class_(children) return e.simplify_op() Expr. simplify = expr_simplify def expr_simplify_op(self): return self.eval() Expr. simplify_up = expr_simplify_op def plus simplify_op(self): - Simplification of Plus expressions. *** # YOUR CODE HERE raise Not ImplementedError() def minus_simplify_op(self): - Simplification of Minus expressions." # YOUR CODE HERE raise Not ImplementedError() def multiply_simplify_op(self): "Simplification of Multiply expressions. # YOUR CODE HERE raise Not ImplementedError() def divide_simplify_op(self): ***Simplification of Divide expressions." # YOUR CODE HERE raise Not ImplementedError() def power_simplify_op(self): ***Simplification of Power expressions." # YOUR CODE HERE raise Not ImplementedError() def logarithm_simplify_op(self): ***Simplification of Logarithm expressions." # YOUR CODE HERE raise Not ImplementedError() def negative_simplify_op(self): **Simplification of Negative expressions. # YOUR CODE HERE raise Not ImplementedError() Plus. Simplify_up = plus simplify_op Minus. Simplify_op = minus_Simplify_op Multiply.simplify_op = multiply_simplify_op Divide. Simplify_op= divide_simplify_op Logarithm.Simplify_op= logarithm_simplify_op Power.simplify_up = power_simplify_op Negative.simplify_up = negative_simplify_op Problem 3: Expression simplification Although we can take the derivatives of various expressions, the results might not be exactly what we were hoping for. For example, the derivative of 5y +1 with respect to y should be 5, but it comes out as Plus (Plus (Multiply(e, V'y'), 5), ). This is equivalent to 5 (because 0 x y=0,0+5 = 5, and 5 +0=5), but it is rather ugly to read: [] e = 5 * Vy') + 1 e.derivative('y') Although calling eval() would help in many cases, in this situation calling eval() on e.derivative('y') would not help, because we do not have a value for the variable (y'). But what we can do instead is implement a method to simplify expressions like this one. For this problem, you will write methods implementing simplification of expressions for each subclass of Expr. You should implement the following simplifications: Plus(@, e) and Plus(e, ) should simplify to e, for any e. Minus(e, o) should simplify to e, for any e. Minus(@, e) should simplify to Negative(e). Multiply(@, e) and Multiply(e, a) should simplify to e, for any e. Multiply(1, e) and Multiply(e, 1) should simplify to e, for any e. Divide (@, e) should simplify to e, for any e. Divide(e, 1) should simplify to e, for any e Power(1, e) should simplify to 1, for any e. Power(e, ) should simplify to 1, for any e. Power(e, 1) should simplify to e, for any e. Logarithm(1) should simplify to e. Negative() should simplify to e. The simplification rules should be applied recursively over the expression, so that v('x') *(1 + ('') * %) should be simplifed to v('x'). To get you started, we have implemented a simplify method for the Expr class, which relies on each subclass having implemented a simplify_op method. Your task is to implement these simplify_op methods for the Plus, Minus, Multiply, Divide, Logarithm, Power, and Negative classes. The methods you write should implement the simplifications described above for each expression type, and return a simplified expression. If none of the above simplifications are possible, each simplify op method should call eval() on the expression. Finally, in order to test your simplify_op implementations, we need to be able to check for expression equality, with a more lenient notion of equality than Python's "same object" notion. The below cell should do the job; be sure to run it before you test your code. I def equality_as_same_types_and_attributes(self, other): return type(self) == type(other) and self._dict__ == other. _dict__ Expr. _e__ = equality_as_same_types_and_attributes def expr_simplify(self): children = [c.simplify() if isinstance(C, Expr) else C for c in self.children] e = self._class_(children) return e.simplify_op() Expr. simplify = expr_simplify def expr_simplify_op(self): return self.eval() Expr. simplify_up = expr_simplify_op def plus simplify_op(self): - Simplification of Plus expressions. *** # YOUR CODE HERE raise Not ImplementedError() def minus_simplify_op(self): - Simplification of Minus expressions." # YOUR CODE HERE raise Not ImplementedError() def multiply_simplify_op(self): "Simplification of Multiply expressions. # YOUR CODE HERE raise Not ImplementedError() def divide_simplify_op(self): ***Simplification of Divide expressions." # YOUR CODE HERE raise Not ImplementedError() def power_simplify_op(self): ***Simplification of Power expressions." # YOUR CODE HERE raise Not ImplementedError() def logarithm_simplify_op(self): ***Simplification of Logarithm expressions." # YOUR CODE HERE raise Not ImplementedError() def negative_simplify_op(self): **Simplification of Negative expressions. # YOUR CODE HERE raise Not ImplementedError() Plus. Simplify_up = plus simplify_op Minus. Simplify_op = minus_Simplify_op Multiply.simplify_op = multiply_simplify_op Divide. Simplify_op= divide_simplify_op Logarithm.Simplify_op= logarithm_simplify_op Power.simplify_up = power_simplify_op Negative.simplify_up = negative_simplify_op