Python Problem: (Finish the function power_op_derivative)

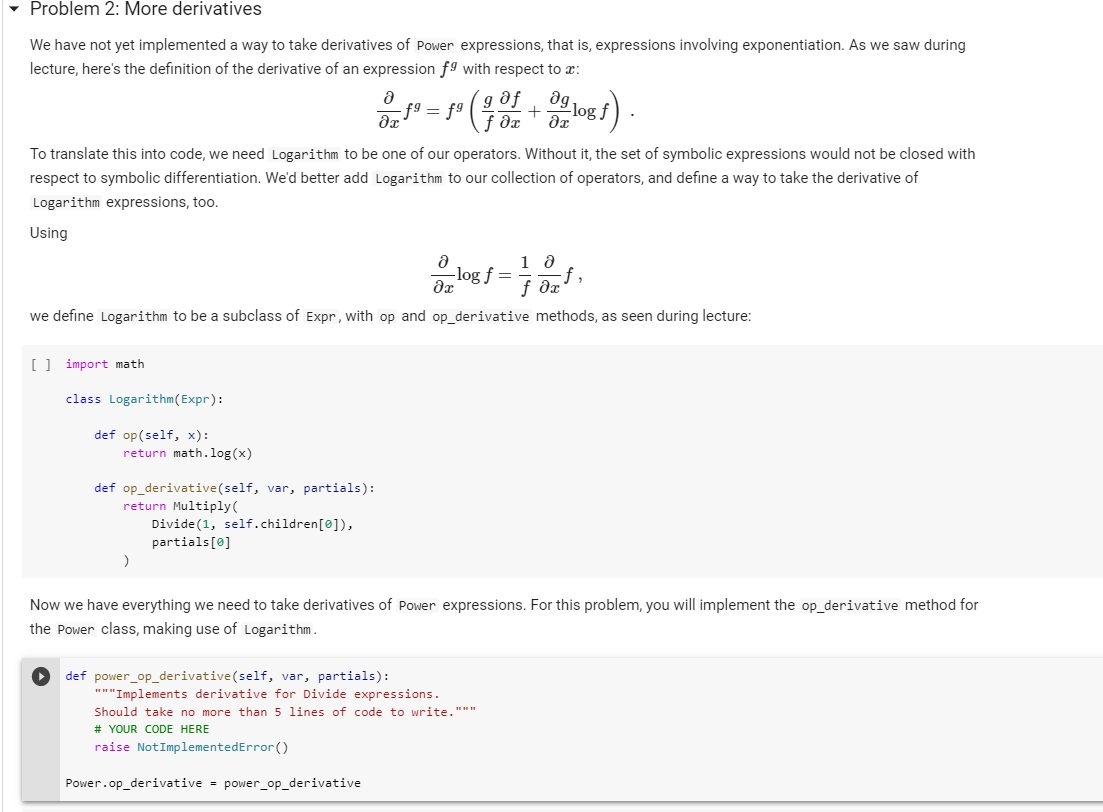
class Plus (Expr): def op (self, x, y): return x + y class Minus (Expr): def op(self, x, y): return x - y class Multiply(Expr): def op (self, x, y): return x * y class Divide(Expr): def op(self, x, y): return x/y class Power(Expr): def op(self, x, y): return x ** y class Negative(Expr): def op (self, x): return -X Problem 2: More derivatives We have not yet implemented a way to take derivatives of Power expressions, that is, expressions involving exponentiation. As we saw during lecture, here's the definition of the derivative of an expression f9 with respect to c: en so = f* ( * 9 1985) To translate this into code, we need Logarithm to be one of our operators. Without it, the set of symbolic expressions would not be closed with respect to symbolic differentiation. We'd better add Logarithm to our collection of operators, and define a way to take the derivative of Logarithm expressions, too. Using we define Logarithm to be a subclass of Expr, with op and op derivative methods, as seen during lecture: [] import math class Logarithm(Expr): def op (self, x): return math.log(x) def op derivative(self, var, partials): return Multiply Divide(1, self.children[@]), partials[@] Now we have everything we need to take derivatives of Power expressions. For this problem, you will implement the op_derivative method for the Power class, making use of Logarithm. def power_op_derivative (self, var, partials): "* "Implements derivative for Divide expressions. Should take no more than 5 lines of code to write." # YOUR CODE HERE raise Not ImplementedError() Power.op_derivative = power_op_derivative class Plus (Expr): def op (self, x, y): return x + y class Minus (Expr): def op(self, x, y): return x - y class Multiply(Expr): def op (self, x, y): return x * y class Divide(Expr): def op(self, x, y): return x/y class Power(Expr): def op(self, x, y): return x ** y class Negative(Expr): def op (self, x): return -X Problem 2: More derivatives We have not yet implemented a way to take derivatives of Power expressions, that is, expressions involving exponentiation. As we saw during lecture, here's the definition of the derivative of an expression f9 with respect to c: en so = f* ( * 9 1985) To translate this into code, we need Logarithm to be one of our operators. Without it, the set of symbolic expressions would not be closed with respect to symbolic differentiation. We'd better add Logarithm to our collection of operators, and define a way to take the derivative of Logarithm expressions, too. Using we define Logarithm to be a subclass of Expr, with op and op derivative methods, as seen during lecture: [] import math class Logarithm(Expr): def op (self, x): return math.log(x) def op derivative(self, var, partials): return Multiply Divide(1, self.children[@]), partials[@] Now we have everything we need to take derivatives of Power expressions. For this problem, you will implement the op_derivative method for the Power class, making use of Logarithm. def power_op_derivative (self, var, partials): "* "Implements derivative for Divide expressions. Should take no more than 5 lines of code to write." # YOUR CODE HERE raise Not ImplementedError() Power.op_derivative = power_op_derivative








