Python Problem:
Starting codes:
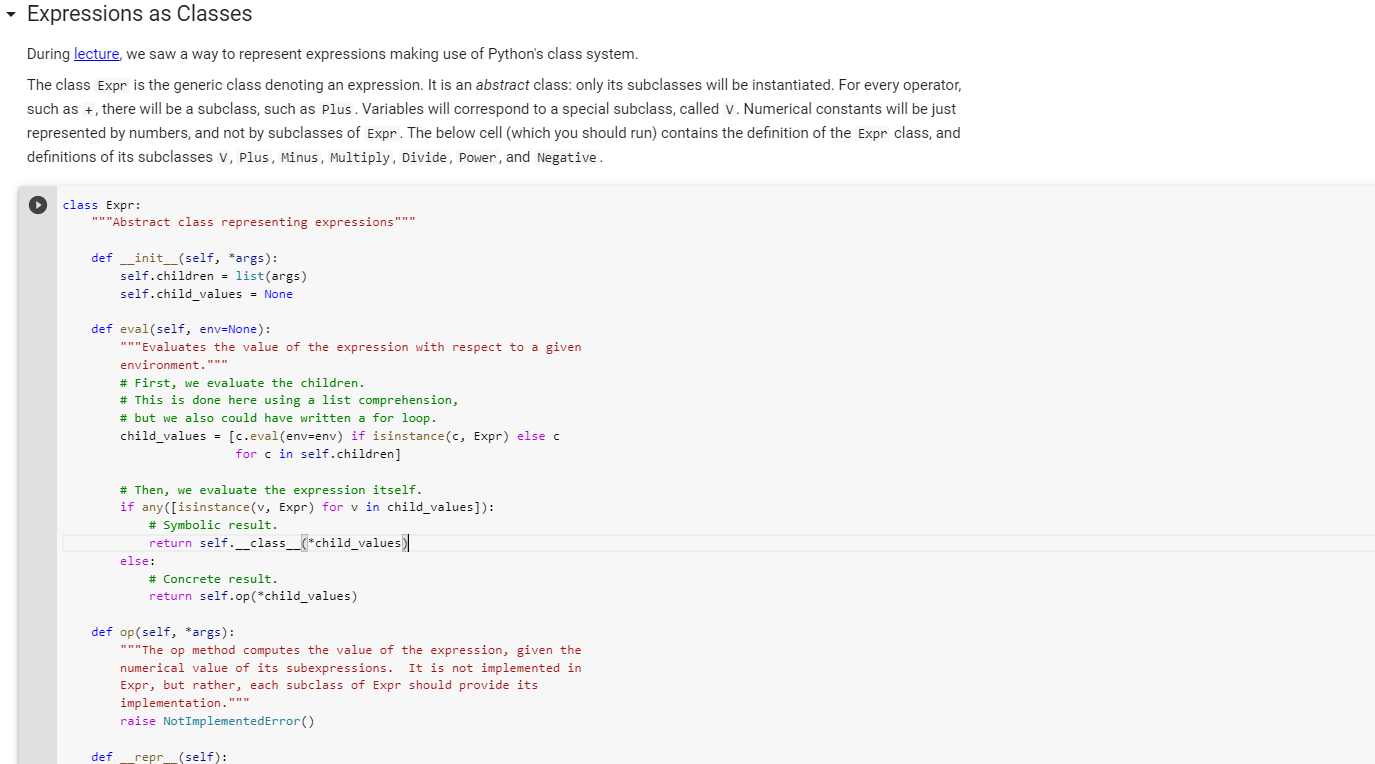
class Expr:
"""Abstract class representing expressions"""
def __init__(self, *args):
self.children = list(args)
self.child_values = None
def eval(self, env=None):
"""Evaluates the value of the expression with respect to a given
environment."""
# First, we evaluate the children.
# This is done here using a list comprehension,
# but we also could have written a for loop.
child_values = [c.eval(env=env) if isinstance(c, Expr) else c
for c in self.children]
# Then, we evaluate the expression itself.
if any([isinstance(v, Expr) for v in child_values]):
# Symbolic result.
return self.__class__(*child_values)
else:
# Concrete result.
return self.op(*child_values)
def op(self, *args):
"""The op method computes the value of the expression, given the
numerical value of its subexpressions. It is not implemented in
Expr, but rather, each subclass of Expr should provide its
implementation."""
raise NotImplementedError()
def __repr__(self):
"""Represents the expression as the name of the class,
followed by all the children in parentheses."""
return "%s(%s)" % (self.__class__.__name__,
', '.join(repr(c) for c in self.children))
# Expression constructors
def __add__(self, other):
return Plus(self, other)
def __radd__(self, other):
return Plus(self, other)
def __sub__(self, other):
return Minus(self, other)
def __rsub__(self, other):
return Minus(other, self)
def __mul__(self, other):
return Multiply(self, other)
def __rmul__(self, other):
return Multiply(other, self)
def __truediv__(self, other):
return Divide(self, other)
def __rtruediv__(self, other):
return Divide(other, self)
def __pow__(self, other):
return Power(self, other)
def __rpow__(self, other):
return Power(other, self)
def __neg__(self):
return Negative(self)
class V(Expr):
"""Variable."""
def __init__(self, *args):
"""Variables must be of type string."""
assert len(args) == 1
assert isinstance(args[0], str)
super().__init__(*args)
def eval(self, env=None):
"""If the variable is in the environment, returns the
value of the variable; otherwise, returns the expression."""
if env is not None and self.children[0] in env:
return env[self.children[0]]
else:
return self
class Plus(Expr):
def op(self, x, y):
return x + y
class Minus(Expr):
def op(self, x, y):
return x - y
class Multiply(Expr):
def op(self, x, y):
return x * y
class Divide(Expr):
def op(self, x, y):
return x / y
class Power(Expr):
def op(self, x, y):
return x ** y
class Negative(Expr):
def op(self, x):
return -x

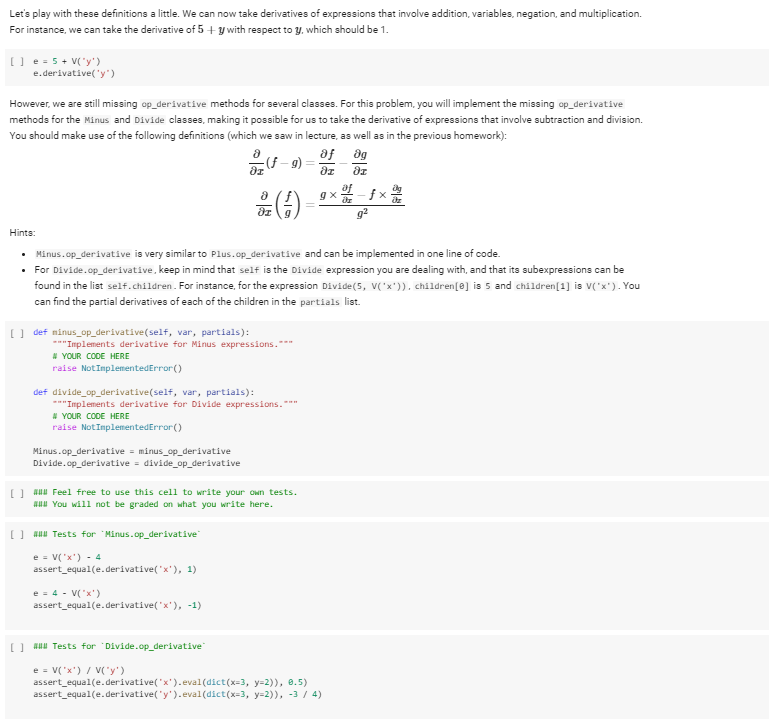
- Expressions as Classes During lecture, we saw a way to represent expressions making use of Python's class system. The class Expr is the generic class denoting an expression. It is an abstract class: only its subclasses will be instantiated. For every operator, such as +, there will be a subclass, such as Plus. Variables will correspond to a special subclass, called v. Numerical constants will be just represented by numbers, and not by subclasses of Expr. The below cell (which you should run) contains the definition of the Expr class, and definitions of its subclasses V, Plus, Minus, Multiply, Divide, Power, and Negative. class Expr: ""Abstract class representing expressions""" def __init__(self, *args): self.children = list(args) self.child_values = None def eval(self, env=None): "Evaluates the value of the expression with respect to a given environment." # First, we evaluate the children. # This is done here using a list comprehension, # but we also could have written a for loop. child_values = [c.eval(env=env) if isinstance (C, Expr) else c for c in self.children] # Then, we evaluate the expression itself. if any([isinstance(v, Expr) for v in child_values]): # Symbolic result. return self._class__(*child_values) else: # Concrete result. return self.op(*child_values) def op(self, *args) : "The op method computes the value of the expression, given the numerical value of its subexpressions. It is not implemented in Expr, but rather, each subclass of Expr should provide its implementation." raise NotImplementedError() def repr_(self): Problem 1: Computing derivatives of expressions During lecture, we wrote a method derivative such that, for an expression e, the method call e derivative('x') returns the derivative of the expression with respect to V('x'). To get the derivative of a composite expression with respect to a variable, we need to get the derivative of the subexpressions with respect to that same variable. Thus, we divide the work as follows: . The method derivative first calls the method derivative for all the subexpressions, that is, the children of the expression, accumulating the results into a list partials (so called because these are partial derivatives) Then, the method derivative calls op derivative. This method is an abstract method of Expr, and is implemented in each subclass (v. Plus, Minus, and so on). The method op_derivative will compute the derivative of the expression, according to the operator type. We defined the derivative method for the Expr class, and we began implementing op derivative for each operator, but during lecture we only wrote op derivative for some of the subclasses of Expr. In particular, we implemented it for the V. Plus, and Multiply subclasses of Expr. Below is the code that defines the derivative methods for the Expr class and the V class, and defines the op_derivative methods for the Plus, Negative, and Multiply subclasses of Expr. How does it work? partials is a list that contains the partial derivatives of every subexpression of an expression, computed in the Expr class. The op_derivative methods for each operator all combine the elements of partials to construct the partial derivative in whichever way is appropriate for that operator. [] def expr_derivative(self, var): ***Computes the derivative of the expression with respect to var.** partials = [(c. derivative(var) if isinstance(c, Expr) else ) for c in self.children] return self.op_derivative(var, partials).eval() def expr_op_derivative(self, var, partials): raise NotImplementedError() # Extends the existing Expr class with the newly defined methods. Expr. derivative = expr_derivative Expr.op_derivative = expr_op_derivative der variable_derivative(self, var): return 1 if self.children[@] == var else @ # Extends the existing V class with the newly defined method. V.derivative = variable_derivative def plus_op_derivative(self, var, partials): return Plus (partials[@], partials[1]) # Extends the existing Plus class...you get the idea. Plus.op_derivative = plus_op_derivative def negative_op_derivative(self, var, partials): return Negative(partials[e]) Negative.op_derivative = negative_op_derivative def multiply_op_derivative(self, var, partials): return Plus Multiply(partials[@], self.children[1]), Multiply(partials[1], self.children[@]) Multiply.op_derivative = multiply_op_derivative Let's play with these definitions a little. We can now take derivatives of expressions that involve addition, variables, negation, and multiplication. For instance, we can take the derivative of 5+ y with respect to y, which should be 1. [] e = 5 + V'y') e.derivative('y") However, we are still missing op derivative methods for several classes. For this problem, you will implement the missing op derivative methods for the Minus and Divide classes, making it possible for us to take the derivative of expressions that involve subtraction and division. You should make use of the following definitions (which we saw in lecture, as well as in the previous homework): of og (- 9) = aj fx Hints: Minus.op_derivative is very similar to Plus.op_derivative and can be implemented in one line of code. For Divide.op_derivative, keep in mind that self is the Divide expression you are dealing with, and that its subexpressions can be found in the list self.children. For instance, for the expression Divide(5, V('x')). Children[@] is 5 and children[1] is v('x'). You can find the partial derivatives of each of the children in the partials list. [ ] def minus_op_derivative(self, var, partials): ***Implements derivative for Minus expressions. # YOUR CODE HERE raise Not ImplementedError() def divide_op_derivative(self, var, partials): **Implements derivative for Divide expressions # YOUR CODE HERE raise Not ImplementedError() Minus.op_derivative = minus_op_derivative Divide.op_derivative = divide_op_derivative [ ] Feel free to use this cell to write your own tests. All You will not be graded on what you write here. D u Tests for "Minus.op_derivative e = V('x') - 4 assert_equal(e.derivative('x'), 1) e = 4 - V('x') assert_equal(e.derivative('x'), -1) All Tests for "Divide.op_derivative e = V('x') / Vy') assert_equal(e.derivative('x').eval(dict(x=3, y=2)), 0.5) assert_equal(e derivative('y').eval(dict(x=3, y=2)), -3/4) - Expressions as Classes During lecture, we saw a way to represent expressions making use of Python's class system. The class Expr is the generic class denoting an expression. It is an abstract class: only its subclasses will be instantiated. For every operator, such as +, there will be a subclass, such as Plus. Variables will correspond to a special subclass, called v. Numerical constants will be just represented by numbers, and not by subclasses of Expr. The below cell (which you should run) contains the definition of the Expr class, and definitions of its subclasses V, Plus, Minus, Multiply, Divide, Power, and Negative. class Expr: ""Abstract class representing expressions""" def __init__(self, *args): self.children = list(args) self.child_values = None def eval(self, env=None): "Evaluates the value of the expression with respect to a given environment." # First, we evaluate the children. # This is done here using a list comprehension, # but we also could have written a for loop. child_values = [c.eval(env=env) if isinstance (C, Expr) else c for c in self.children] # Then, we evaluate the expression itself. if any([isinstance(v, Expr) for v in child_values]): # Symbolic result. return self._class__(*child_values) else: # Concrete result. return self.op(*child_values) def op(self, *args) : "The op method computes the value of the expression, given the numerical value of its subexpressions. It is not implemented in Expr, but rather, each subclass of Expr should provide its implementation." raise NotImplementedError() def repr_(self): Problem 1: Computing derivatives of expressions During lecture, we wrote a method derivative such that, for an expression e, the method call e derivative('x') returns the derivative of the expression with respect to V('x'). To get the derivative of a composite expression with respect to a variable, we need to get the derivative of the subexpressions with respect to that same variable. Thus, we divide the work as follows: . The method derivative first calls the method derivative for all the subexpressions, that is, the children of the expression, accumulating the results into a list partials (so called because these are partial derivatives) Then, the method derivative calls op derivative. This method is an abstract method of Expr, and is implemented in each subclass (v. Plus, Minus, and so on). The method op_derivative will compute the derivative of the expression, according to the operator type. We defined the derivative method for the Expr class, and we began implementing op derivative for each operator, but during lecture we only wrote op derivative for some of the subclasses of Expr. In particular, we implemented it for the V. Plus, and Multiply subclasses of Expr. Below is the code that defines the derivative methods for the Expr class and the V class, and defines the op_derivative methods for the Plus, Negative, and Multiply subclasses of Expr. How does it work? partials is a list that contains the partial derivatives of every subexpression of an expression, computed in the Expr class. The op_derivative methods for each operator all combine the elements of partials to construct the partial derivative in whichever way is appropriate for that operator. [] def expr_derivative(self, var): ***Computes the derivative of the expression with respect to var.** partials = [(c. derivative(var) if isinstance(c, Expr) else ) for c in self.children] return self.op_derivative(var, partials).eval() def expr_op_derivative(self, var, partials): raise NotImplementedError() # Extends the existing Expr class with the newly defined methods. Expr. derivative = expr_derivative Expr.op_derivative = expr_op_derivative der variable_derivative(self, var): return 1 if self.children[@] == var else @ # Extends the existing V class with the newly defined method. V.derivative = variable_derivative def plus_op_derivative(self, var, partials): return Plus (partials[@], partials[1]) # Extends the existing Plus class...you get the idea. Plus.op_derivative = plus_op_derivative def negative_op_derivative(self, var, partials): return Negative(partials[e]) Negative.op_derivative = negative_op_derivative def multiply_op_derivative(self, var, partials): return Plus Multiply(partials[@], self.children[1]), Multiply(partials[1], self.children[@]) Multiply.op_derivative = multiply_op_derivative Let's play with these definitions a little. We can now take derivatives of expressions that involve addition, variables, negation, and multiplication. For instance, we can take the derivative of 5+ y with respect to y, which should be 1. [] e = 5 + V'y') e.derivative('y") However, we are still missing op derivative methods for several classes. For this problem, you will implement the missing op derivative methods for the Minus and Divide classes, making it possible for us to take the derivative of expressions that involve subtraction and division. You should make use of the following definitions (which we saw in lecture, as well as in the previous homework): of og (- 9) = aj fx Hints: Minus.op_derivative is very similar to Plus.op_derivative and can be implemented in one line of code. For Divide.op_derivative, keep in mind that self is the Divide expression you are dealing with, and that its subexpressions can be found in the list self.children. For instance, for the expression Divide(5, V('x')). Children[@] is 5 and children[1] is v('x'). You can find the partial derivatives of each of the children in the partials list. [ ] def minus_op_derivative(self, var, partials): ***Implements derivative for Minus expressions. # YOUR CODE HERE raise Not ImplementedError() def divide_op_derivative(self, var, partials): **Implements derivative for Divide expressions # YOUR CODE HERE raise Not ImplementedError() Minus.op_derivative = minus_op_derivative Divide.op_derivative = divide_op_derivative [ ] Feel free to use this cell to write your own tests. All You will not be graded on what you write here. D u Tests for "Minus.op_derivative e = V('x') - 4 assert_equal(e.derivative('x'), 1) e = 4 - V('x') assert_equal(e.derivative('x'), -1) All Tests for "Divide.op_derivative e = V('x') / Vy') assert_equal(e.derivative('x').eval(dict(x=3, y=2)), 0.5) assert_equal(e derivative('y').eval(dict(x=3, y=2)), -3/4)









