Python Programming

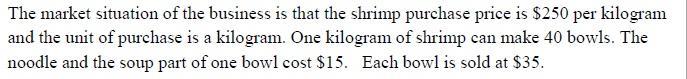
# import the random module import random

# import the time module import time

# probability information about the business bowlSalesTuple = (100, 150, 200, 250, 300, 350, 400, 450, 500, 550) probabilitiesTuple = (0.01, 0.03, 0.08, 0.12, 0.18, 0.20, 0.21, 0.11, 0.04, 0.02)

def randBowlSold(): pass # ENTER YOUR CODE HERE

def simulateOneDay(shrimpOrdered): pass # ENTER YOUR CODE HERE

def findMaxProfit(): pass # ENTER YOUR CODE HERE

# Set a fixed random seed random.seed(0) # Call function to find results findMaxProfit()

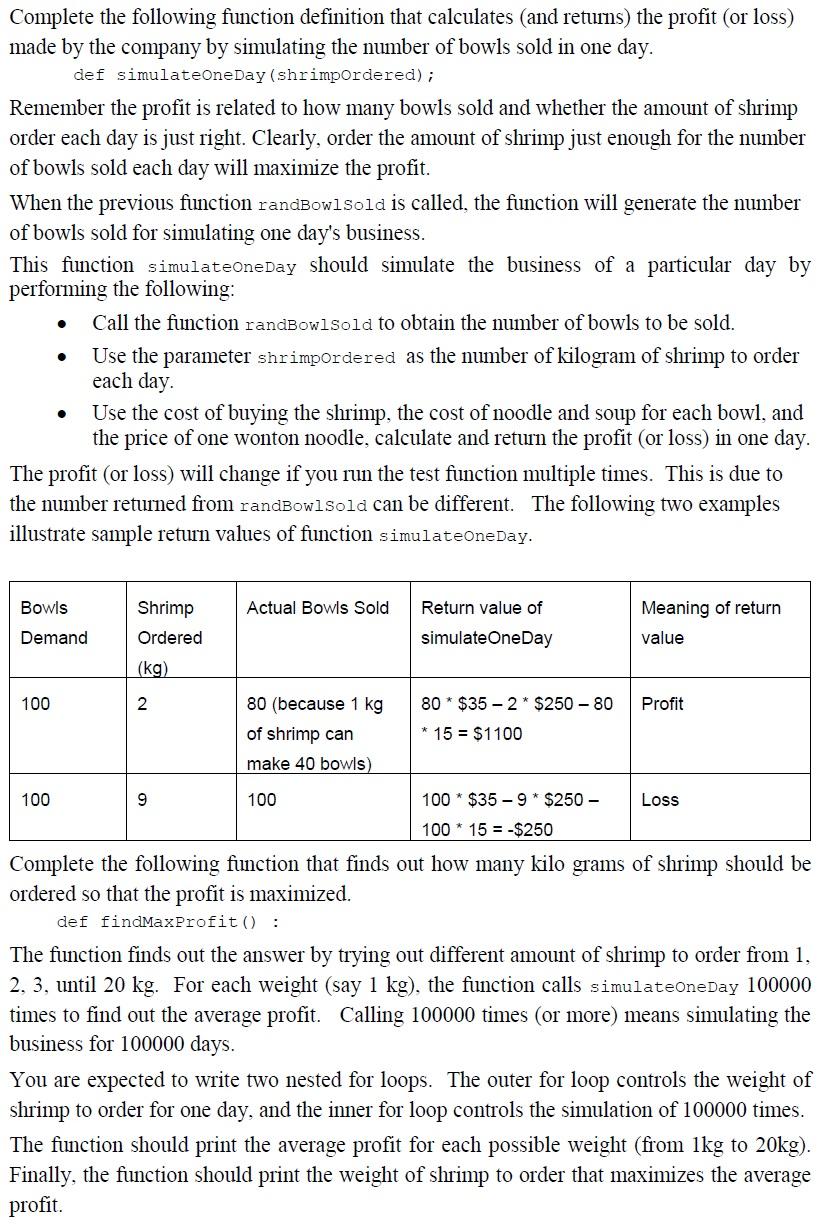
The market situation of the business is that the shrimp purchase price is $250 per kilogram and the unit of purchase is a kilogram. One kilogram of shrimp can make 40 bowls. The noodle and the soup part of one bowl cost $15. Each bowl is sold at $35. The first step involves generating the number of bowls sold in one day. Clearly there is a fluctuation from one day to the next, but according to past statistics, estimation can be made. Complete the following definition of the function that randomly returns one of the ten numbers according to probabilities shown in the following list. def randBowlsold() : The ten numbers and the probabilities of their generation are given in the table below. Passengers Probabilities 100 0.01 150 0.03 200 0.08 250 300 0.18 350 0.20 400 0.21 450 0.11 500 0.04 550 0.02 According to the above table, the function should have the probability of 0.08 (8 in 100 chance) of returning 200 (selling 200 bowls in a day), and the probability of 0.20 (20 in 100 chance) returning 350, etc. 0.12 Complete the following function definition that calculates (and returns) the profit (or loss) made by the company by simulating the number of bowls sold in one day. def simulateOneDay (shrimpordered); Remember the profit is related to how many bowls sold and whether the amount of shrimp order each day is just right. Clearly, order the amount of shrimp just enough for the number of bowls sold each day will maximize the profit. When the previous function randBowlsold is called the function will generate the number of bowls sold for simulating one day's business. This function simulateOneDay should simulate the business of a particular day by performing the following: Call the function randBowlsold to obtain the number of bowls to be sold. Use the parameter shrimpordered as the number of kilogram of shrimp to order each day. Use the cost of buying the shrimp, the cost of noodle and soup for each bowl, and the price of one wonton noodle, calculate and return the profit (or loss) in one day. The profit (or loss) will change if you run the test function multiple times. This is due to the number returned from randBowlsold can be different. The following two examples illustrate sample return values of function simulateoneDay. . . Bowls Actual Bowls Sold Return value of Shrimp Ordered (kg) Meaning of return value Demand simulate OneDay 100 2 Profit 80 (because 1 kg of shrimp can make 40 bowls) 80 * $35 - 2* $250 - 80 * 15 = $1100 100 9 100 100 * $35 -9 * $250 - Loss 100 * 15 = -$250 Complete the following function that finds out how many kilo grams of shrimp should be ordered so that the profit is maximized. def findMaxProfit(): The function finds out the answer by trying out different amount of shrimp to order from 1, 2, 3, until 20 kg. For each weight (say 1 kg), the function calls simulateoneDay 100000 times to find out the average profit. Calling 100000 times (or more) means simulating the business for 100000 days. You are expected to write two nested for loops. The outer for loop controls the weight of shrimp to order for one day, and the inner for loop controls the simulation of 100000 times. The function should print the average profit for each possible weight (from 1kg to 20kg). Finally, the function should print the weight of shrimp to order that maximizes the average profit. The market situation of the business is that the shrimp purchase price is $250 per kilogram and the unit of purchase is a kilogram. One kilogram of shrimp can make 40 bowls. The noodle and the soup part of one bowl cost $15. Each bowl is sold at $35. The first step involves generating the number of bowls sold in one day. Clearly there is a fluctuation from one day to the next, but according to past statistics, estimation can be made. Complete the following definition of the function that randomly returns one of the ten numbers according to probabilities shown in the following list. def randBowlsold() : The ten numbers and the probabilities of their generation are given in the table below. Passengers Probabilities 100 0.01 150 0.03 200 0.08 250 300 0.18 350 0.20 400 0.21 450 0.11 500 0.04 550 0.02 According to the above table, the function should have the probability of 0.08 (8 in 100 chance) of returning 200 (selling 200 bowls in a day), and the probability of 0.20 (20 in 100 chance) returning 350, etc. 0.12 Complete the following function definition that calculates (and returns) the profit (or loss) made by the company by simulating the number of bowls sold in one day. def simulateOneDay (shrimpordered); Remember the profit is related to how many bowls sold and whether the amount of shrimp order each day is just right. Clearly, order the amount of shrimp just enough for the number of bowls sold each day will maximize the profit. When the previous function randBowlsold is called the function will generate the number of bowls sold for simulating one day's business. This function simulateOneDay should simulate the business of a particular day by performing the following: Call the function randBowlsold to obtain the number of bowls to be sold. Use the parameter shrimpordered as the number of kilogram of shrimp to order each day. Use the cost of buying the shrimp, the cost of noodle and soup for each bowl, and the price of one wonton noodle, calculate and return the profit (or loss) in one day. The profit (or loss) will change if you run the test function multiple times. This is due to the number returned from randBowlsold can be different. The following two examples illustrate sample return values of function simulateoneDay. . . Bowls Actual Bowls Sold Return value of Shrimp Ordered (kg) Meaning of return value Demand simulate OneDay 100 2 Profit 80 (because 1 kg of shrimp can make 40 bowls) 80 * $35 - 2* $250 - 80 * 15 = $1100 100 9 100 100 * $35 -9 * $250 - Loss 100 * 15 = -$250 Complete the following function that finds out how many kilo grams of shrimp should be ordered so that the profit is maximized. def findMaxProfit(): The function finds out the answer by trying out different amount of shrimp to order from 1, 2, 3, until 20 kg. For each weight (say 1 kg), the function calls simulateoneDay 100000 times to find out the average profit. Calling 100000 times (or more) means simulating the business for 100000 days. You are expected to write two nested for loops. The outer for loop controls the weight of shrimp to order for one day, and the inner for loop controls the simulation of 100000 times. The function should print the average profit for each possible weight (from 1kg to 20kg). Finally, the function should print the weight of shrimp to order that maximizes the average profit