Python programming problem using MATPLOT library in NumPy. Below is my code. I tried to make an array that is a function of time so that it should function like a traditional array to array plot in matplotlib. I keep getting this same error. I am totally stuck and some help would be greatly appreciated.

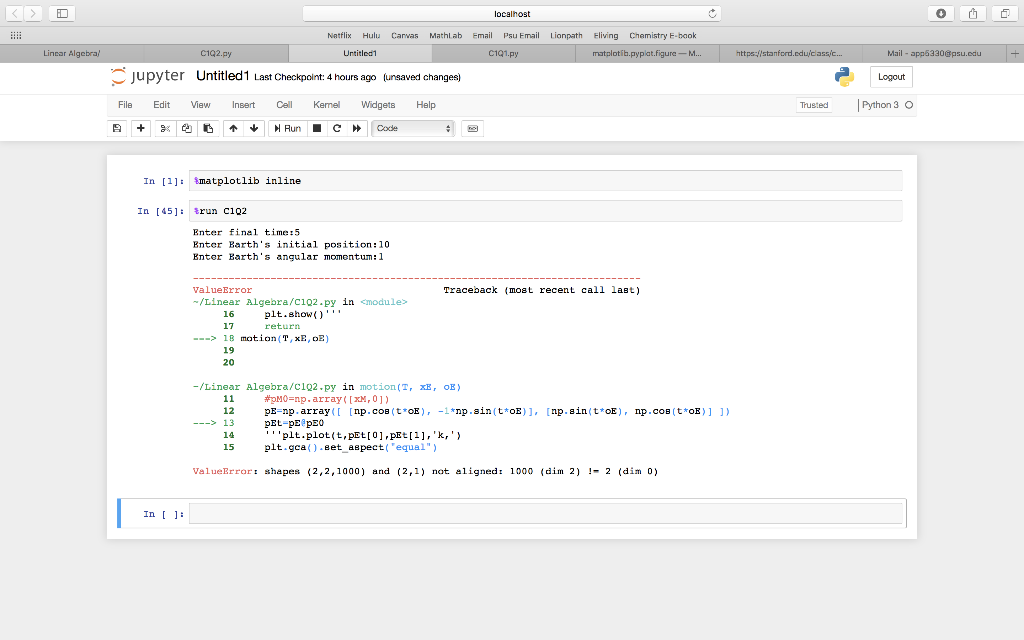
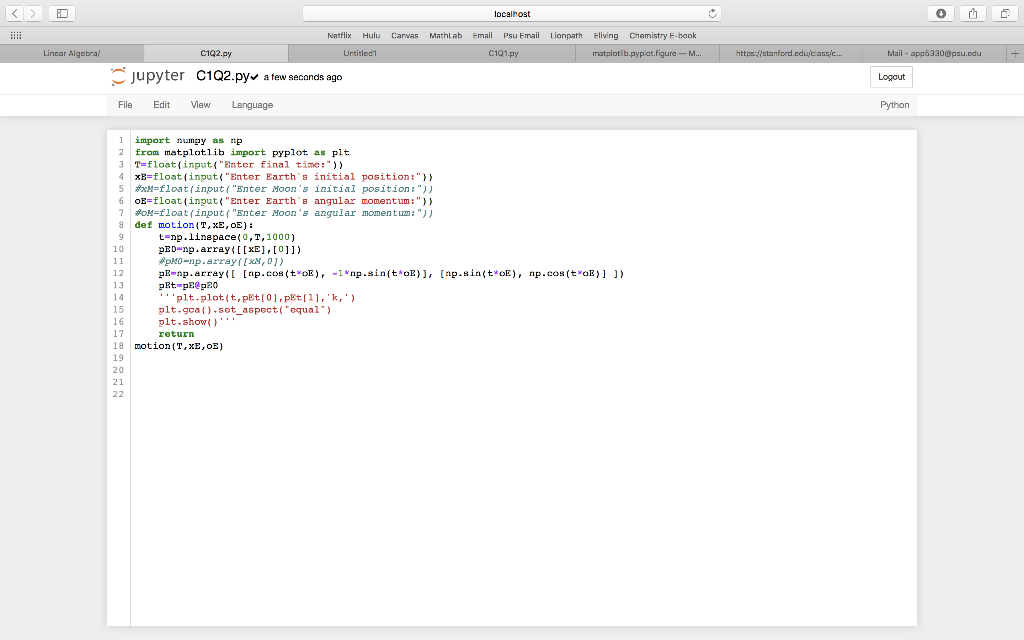
Problem 2. The moon orbits the earth while the earth orbits the sun. Assuming circular orbits, we can compute the trajectories of both the earth and the moon using only linear and affine transformations Assume an orientation where both the earth and moon travel counterclockwise, with the sun at the origin. Let pe (t) and pm (t) be the positions of the earth and the moon at time t, respectively, and let we and wm be each celestial body's angular momentum. For a particular time t, we calculate pe (t) and p,m (t) with the following steps 1. Compute pe(t) by rotating the initial vector pe (0) counterclockwise about the origin by twe radians 2. Calculate the position of the moon relative to the earth at time t by rotating the vector Pm (0) - pe (0) counterclockwise about the origin by twm radians 3. To compute pm (t), translate the vector resulting from the previous step by pe (t) Write a function that accepts a final time T, initial positions re and m, and the angular (xm, 0), plot momenta we and wm Assuming initial positions pe(0(e, 0) and pm (0 Pe(t) and pm (t) over the time interval t E [0, T Setting T e 10, m , we1, and wm 13, your plot should resemble the following figure (fix the aspect ratio with ax.set_aspect ("equal")). Note that a more celestially accurate figure would use re400, m- 401 (the interested reader should see http://www.math.nus.edu.sg/aslaksen/teaching/convex.html) 10 0 5 -Earth Moon 10 10 0 5 10 localhost 0 Natflix Hulu Carvas Mathl ab Email Psu Email Lionpath Eliving Chemistry E-book Lincar Algebra Untitled1 C1Q .figure ttps Mail Jupyter Untitled! Last Checkpoint: 4 hours ago tureaved changes) Logout File Edit Vie sert Cel Kemel Widgets Help Trusted Python 3 O In 1 smatplotlib inline In [45 run C102 Enter final time:5 Enter E rth's initial pos ition : 10 Enter Barth's angular momentum:1 alueError /Linear Algebra/C102.py in cmodules Traceback (moat recent call last) 16 plt.show) return 17 1B motion (T, xE, oE) 19 20 -/Linear Algebra/c1Q2 py in motion(T x, o -13 14 15 plt.plot(t,pEtI01,pE[11.'k,' plt.gca() et aspect( equal") aluerrort shapes 2,2,1000) and (2,1) not aligned: 1000 (dim 2) !-2 (dim 0) In 1 localhost Natflix Hulu Carvas Mathl ab Email Psu Email Lionpath Eliving Chemistry E-book Lincar Algebra C1Q2.py Untitled1 .figure Mail jupyter C102.py atew seconds ago Logout File Edit View Language Python 1 import numpy as np 2 from matplotlib import pyplot as plt 3T-float(input"Enter final timc:") x8=float (input("Enter Earth's initial position:")) 5 xM-float(input "Enter Moon's initial position:" 6oE-float(input "Enter Earth's angular momentum:")) #0M-float (input ("Enter Moon's def motion (T, xE, oE) angular momentum:")) 8 t-np.linapace(, T,1000) pED-np.array xE],[0]]) pHO np.arrayfM,0) pE-np.array [np.cos(t E1*np.sin(t oE), [np.sin(t*oE), np.cos(t oE pEt=pE@pE0 10 12 ) 14 15 16 17 18 motion (T.xE,oE) 19 20 21 plt.plot(t,pEtIO] pEt1l,k plt.gca().sot_aspect plt, show return equal Problem 2. The moon orbits the earth while the earth orbits the sun. Assuming circular orbits, we can compute the trajectories of both the earth and the moon using only linear and affine transformations Assume an orientation where both the earth and moon travel counterclockwise, with the sun at the origin. Let pe (t) and pm (t) be the positions of the earth and the moon at time t, respectively, and let we and wm be each celestial body's angular momentum. For a particular time t, we calculate pe (t) and p,m (t) with the following steps 1. Compute pe(t) by rotating the initial vector pe (0) counterclockwise about the origin by twe radians 2. Calculate the position of the moon relative to the earth at time t by rotating the vector Pm (0) - pe (0) counterclockwise about the origin by twm radians 3. To compute pm (t), translate the vector resulting from the previous step by pe (t) Write a function that accepts a final time T, initial positions re and m, and the angular (xm, 0), plot momenta we and wm Assuming initial positions pe(0(e, 0) and pm (0 Pe(t) and pm (t) over the time interval t E [0, T Setting T e 10, m , we1, and wm 13, your plot should resemble the following figure (fix the aspect ratio with ax.set_aspect ("equal")). Note that a more celestially accurate figure would use re400, m- 401 (the interested reader should see http://www.math.nus.edu.sg/aslaksen/teaching/convex.html) 10 0 5 -Earth Moon 10 10 0 5 10 localhost 0 Natflix Hulu Carvas Mathl ab Email Psu Email Lionpath Eliving Chemistry E-book Lincar Algebra Untitled1 C1Q .figure ttps Mail Jupyter Untitled! Last Checkpoint: 4 hours ago tureaved changes) Logout File Edit Vie sert Cel Kemel Widgets Help Trusted Python 3 O In 1 smatplotlib inline In [45 run C102 Enter final time:5 Enter E rth's initial pos ition : 10 Enter Barth's angular momentum:1 alueError /Linear Algebra/C102.py in cmodules Traceback (moat recent call last) 16 plt.show) return 17 1B motion (T, xE, oE) 19 20 -/Linear Algebra/c1Q2 py in motion(T x, o -13 14 15 plt.plot(t,pEtI01,pE[11.'k,' plt.gca() et aspect( equal") aluerrort shapes 2,2,1000) and (2,1) not aligned: 1000 (dim 2) !-2 (dim 0) In 1 localhost Natflix Hulu Carvas Mathl ab Email Psu Email Lionpath Eliving Chemistry E-book Lincar Algebra C1Q2.py Untitled1 .figure Mail jupyter C102.py atew seconds ago Logout File Edit View Language Python 1 import numpy as np 2 from matplotlib import pyplot as plt 3T-float(input"Enter final timc:") x8=float (input("Enter Earth's initial position:")) 5 xM-float(input "Enter Moon's initial position:" 6oE-float(input "Enter Earth's angular momentum:")) #0M-float (input ("Enter Moon's def motion (T, xE, oE) angular momentum:")) 8 t-np.linapace(, T,1000) pED-np.array xE],[0]]) pHO np.arrayfM,0) pE-np.array [np.cos(t E1*np.sin(t oE), [np.sin(t*oE), np.cos(t oE pEt=pE@pE0 10 12 ) 14 15 16 17 18 motion (T.xE,oE) 19 20 21 plt.plot(t,pEtIO] pEt1l,k plt.gca().sot_aspect plt, show return equal









