python

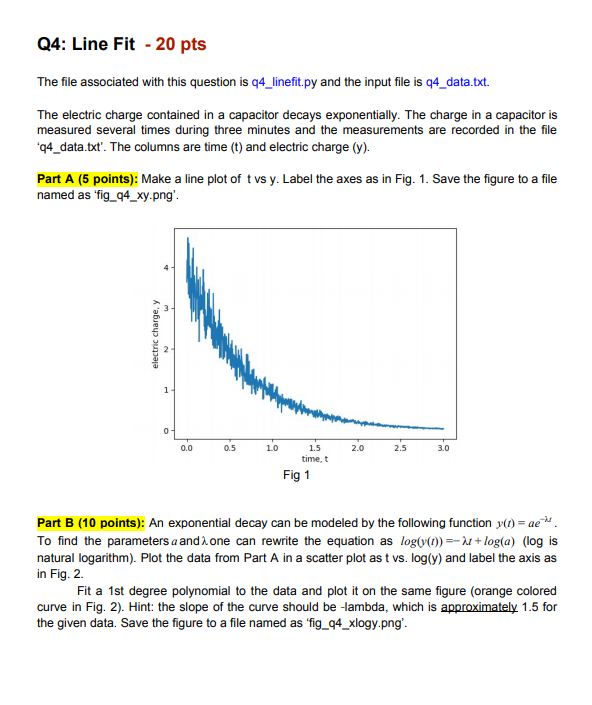
Q4: Line Fit - 20 pts The file associated with this question is 24_linefit.py and the input file is 04_data.txt. The electric charge contained in a capacitor decays exponentially. The charge in a capacitor is measured several times during three minutes and the measurements are recorded in the file *94_data.txt'. The columns are time (t) and electric charge (y). Part A (5 points): Make a line plot of t vs y. Label the axes as in Fig. 1. Save the figure to a file named as fig_94_xy.png' electric charge. Y 1 0 0.0 0.5 1.0 2.0 2.5 3.0 1.5 time,t Fig 1 Part B (10 points): An exponential decay can be modeled by the following function y(t) = ae. To find the parameters a anda one can rewrite the equation as log(y(0) -- +log(a) (log is natural logarithm). Plot the data from Part A in a scatter plot as t vs. log(y) and label the axis as in Fig. 2. Fit a 1st degree polynomial to the data and plot it on the same figure (orange colored curve in Fig. 2). Hint: the slope of the curve should be -lambda, which is approximately 1.5 for the given data. Save the figure to a file named as fig_94_xlogy.png' Q4: Line Fit - 20 pts The file associated with this question is 24_linefit.py and the input file is 04_data.txt. The electric charge contained in a capacitor decays exponentially. The charge in a capacitor is measured several times during three minutes and the measurements are recorded in the file *94_data.txt'. The columns are time (t) and electric charge (y). Part A (5 points): Make a line plot of t vs y. Label the axes as in Fig. 1. Save the figure to a file named as fig_94_xy.png' electric charge. Y 1 0 0.0 0.5 1.0 2.0 2.5 3.0 1.5 time,t Fig 1 Part B (10 points): An exponential decay can be modeled by the following function y(t) = ae. To find the parameters a anda one can rewrite the equation as log(y(0) -- +log(a) (log is natural logarithm). Plot the data from Part A in a scatter plot as t vs. log(y) and label the axis as in Fig. 2. Fit a 1st degree polynomial to the data and plot it on the same figure (orange colored curve in Fig. 2). Hint: the slope of the curve should be -lambda, which is approximately 1.5 for the given data. Save the figure to a file named as fig_94_xlogy.png