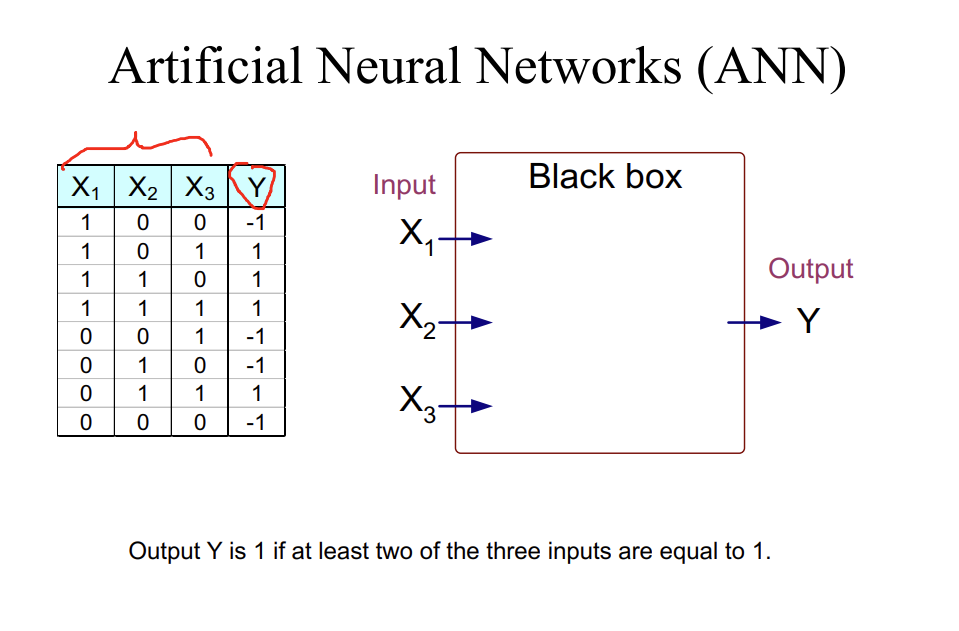
Question: Q1: Consider the same data we used in our lecture. Answer the following questions: X1 0 X2 Homework 4 September 30, 2023 X3 X4

![X1 0 1 1 0 X2 0 1 0 1 Y -1 1 1 -1 e =^[yi-f(w(k),x;)] 2 w(k+1) = w(k) + ex ; Example sign(x)={ : learning](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c25dd7442_3336523c25dcf54f.jpg)
![X1 1 0 0 1 1 X2 0 1 0 1 1 1 1 Adding XO Example Y -1 1 1 -1 f(w,x) -1 -1 -1 -1 e =^[yi-f(w(k),xi)] 2 w(k+1)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c25e86631_3346523c25e6e5cc.jpg)
![X1 0 0 X2 X0 1 1 1 1 0 1 0 1 1 1 Adding XO Example Y -1 1 1 -1 f(w,x) -1 -1 -1 -1 A[yi-f(w(k),x;)] 2 w(k+1) =](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c25f07642_3356523c25f038d1.jpg)
![X1 0 1 1 0 X2 Y 0 -1 1 1 0 1 1 -1 f(w,x) -1 -1 (conflict) -1 -1 [yi(w(k),x;)] e= 2 w(k+1) = w(k) + ex; ;](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c25f85dab_3356523c25f81f13.jpg)
![X1 0 1 X2 0 0 1 1 1 0 1 w (k+1) 1 1 1 Y -1 1 1 -1 ^[Yi-JW' ,xi)] 2 f(w,x) 1 1 Example 1(conflict) f(w(k), x)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c26009d17_3366523c26005ba6.jpg)
![X1 0 0 1 1 1 0 X2 e 1 0 1 1 ^|Yi-J 1 1 Y -1 1 1 -1 f(w,x) -1 1 1 xi)] 2 w(k+1) = w(k) + ex ; Example 1](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c260a2efc_3366523c2609f15a.jpg)
![X1 0 1 1 0 e X2 0 1 1 1 0 1 1 1 Y w(k+1) = -1 1 1 -1 f(w,x) -1 -1(conflict) -1 Example -1 ^[YiJW`Xi)] 2 w(k)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c2613af20_3376523c261374b6.jpg)
![X1 0 0 1 1 1 0 e X2 Y f(w,x) 1 1 0 1 1 1 -1 1 1 -1 ^|Yi-J ^ [YiJ (W,Xi)] -1 1 1 Example 1(conflict) 2 w(k+1)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c261aef4a_3376523c261ab46d.jpg)
![X1 X2 Y 0 0 -1 -1 1 1 1 1 1 0 0 1 f(w,x) 1 -1 1 -1 e = [yi(w(k),xi)] 2 w(k+1) = w(k) + ex; ; Example 1](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/6523c262364e5_3386523c26232540.jpg)
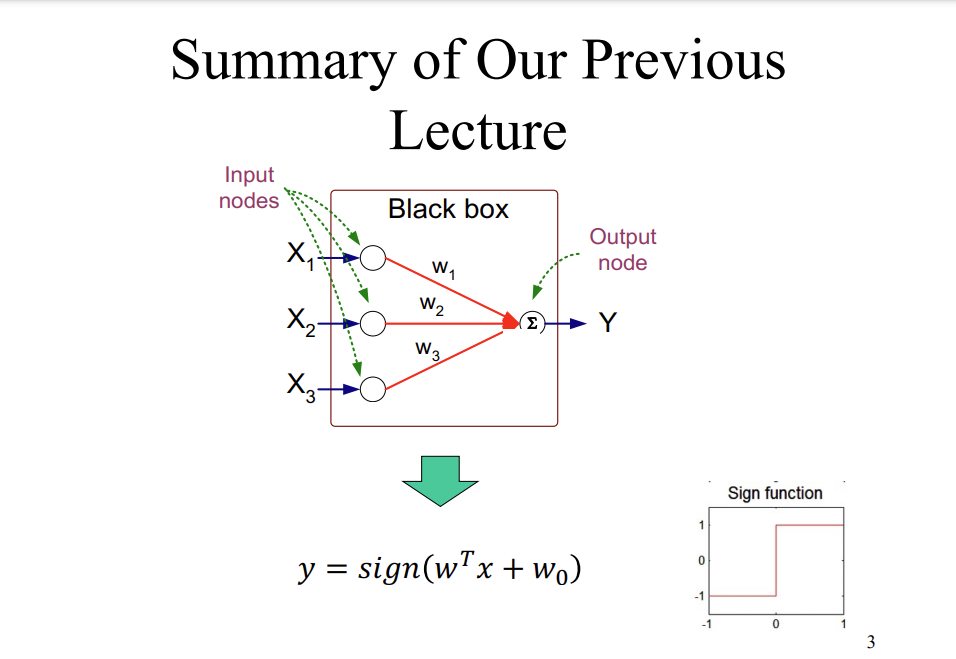
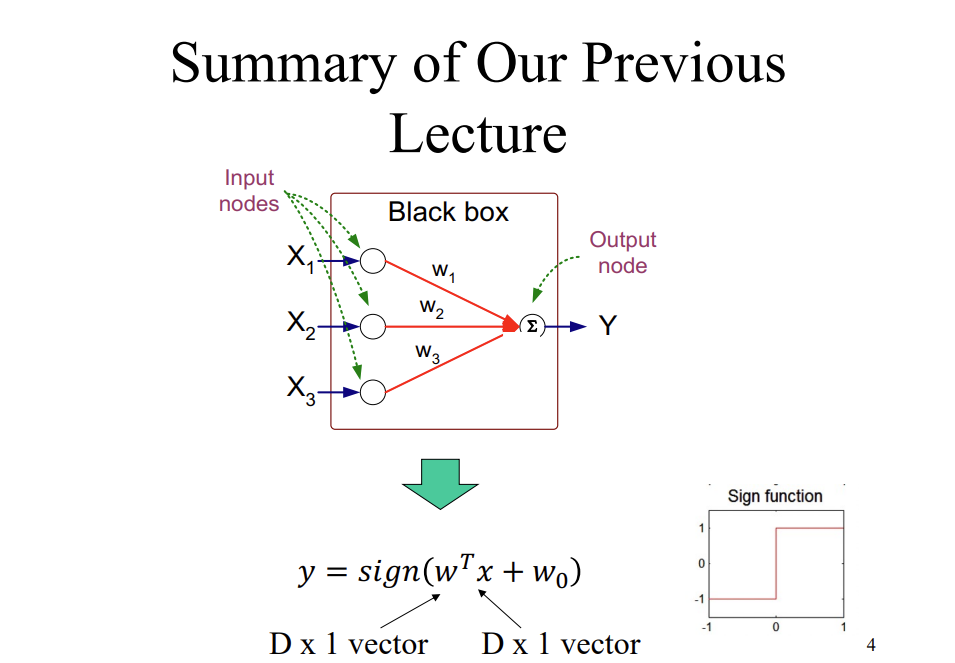
Q1: Consider the same data we used in our lecture. Answer the following questions: X1 0 X2 Homework 4 September 30, 2023 X3 X4 1 1 y 0 class 0 -1 1 1 -1 0 1 1 Using the gradient descend format we discussed in Week 5 lecture (see slides) to train a perceptron model y = sign(wx+wo) with X = 0.2 and w = [-0.5, -0.5, 0.5] == X 1 1 1 1 0 0 0 0 Artificial Neural Networks (ANN) X2 X3 Y 0 -1 1 1 0 1 1 -1 0 0 1 1 0 1 1 0 1 1 0 -1 1 1 0 -1 Input X X X3- Black box Output Y Output Y is 1 if at least two of the three inputs are equal to 1. Summary of Our Previous Lecture Input nodes X X- X3- Black box W W2 W3 Output node Y y = sign(wx + wo) 1 0 -1 -1 Sign function 1 3 Summary of Our Previous Lecture Input nodes X X X3- Black box W W2 W3 Output node (2) Y y = sign (wx + wo) D x 1 vector D x 1 vector 0 -1 -1 Sign function 0 4 X1 0 1 1 0 X2 0 1 0 1 Y -1 1 1 -1 e =^[yi-f(w(k),x;)] 2 w(k+1) = w(k) + ex ; Example sign(x)={ : learning rate 1 -1 x > 0 x 0 f(wk),x) = sign(w(k) T w(0) = [0,0,0] xi + w(k)) X1 1 0 0 1 1 X2 0 1 0 1 1 1 1 Adding XO Example Y -1 1 1 -1 f(w,x) -1 -1 -1 -1 e =^[yi-f(w(k),xi)] 2 w(k+1) = w(k) + ex ; 1 sign(x)={ -1 : learning rate x > 0 x 0 < f(w(K), x) = sign(w(k)T; xi +w(k)) w(0) = [0,0,0] X1 0 0 X2 X0 1 1 1 1 0 1 0 1 1 1 Adding XO Example Y -1 1 1 -1 f(w,x) -1 -1 -1 -1 A[yi-f(w(k),x;)] 2 w(k+1) = w(k) + ex; ; 1 sign(x)={ -1 : learning rate f(w(k), x) = sign(w(K)T xi + w(k)) Xi x > 0 x 0 w (0) = = [0,0,0] X1 0 1 1 0 X2 Y 0 -1 1 1 0 1 1 -1 f(w,x) -1 -1 (conflict) -1 -1 [yi(w(k),x;)] e= 2 w(k+1) = w(k) + ex ; Example w (1) sign(x)={ : learning rate 1 -1 f(wk),x) = sign(w(k)" x w (0) = [0,0,0] x > 0 x 0 xi + w (k)) 10.21 -8+08-6 +0.2 1 0.2 L0.2J X1 0 1 X2 0 0 1 1 1 0 1 w (k+1) 1 1 1 Y -1 1 1 -1 ^[Yi-JW ,Xi)] f(w,x) 1 1 Example 1(conflict) f(w(k), x) = sign(w(k) * x +w(K)) w() = [0.2, 0.2,0.2] 1 2 w(k) + exi ; w (2) : learning rate 1 sign(x)={_ -1 [0.2] 3-08-6 0.2 0 = x > 0 x 0 = 0.2 -0.2 L0.2J [0.2] 0.2 X1 0 0 1 1 1 0 X2 e 1 0 1 1 ^|Yi-J 1 1 Y -1 1 1 -1 f(w,x) -1 1 1 xi)] 2 w(k+1) = w(k) + ex ; Example 1 (conflict) w (3) sign(x)={ : learning rate 1 -1 f(w(k),x;) = sign(w(k)T, w() = [0.2, 0.2,0] x > 0 x 0 10.21 0.2 - 0.2 1 0 .1 xi + w(K)) 0.2 0 -0.2. X1 0 1 1 0 e X2 0 1 1 1 0 1 1 1 Y w(k+1) = -1 1 1 -1 f(w,x) -1 -1(conflict) -1 Example -1 ^[YiJ\W\Xi)] 2 w(k) = w(k) + ex ; w(4) 1 sign(x)={_ 1 f(w(k), xi) = sign(w(k) T x + w(K)) w () = [0.2, 0, 0.2] : learning rate = x > 0 x 0 0.2 []+ 0 -0.2] +0.2 1 = 0.41 0.2 0 X1 0 0 1 1 1 0 e X2 Y f(w,x) 1 1 0 1 1 1 -1 1 1 -1 ^|Yi-J ^ [YiJ (W,Xi)] -1 1 1 Example 1(conflict) 2 w(k+1) = w(k) + ex ; w (5) : learning rate 1 sign(x)={ -1 T f(w (k), x) = sign(w(k) + x + w(K)) w(4) = [0.4, 0.2,0] = x > 0 x 0 [0.4 0.2 0 0.4 H-] = 0 -0.2. 0.2 1 X1 X2 Y 0 0 -1 -1 1 1 1 1 1 0 0 1 f(w,x) 1 -1 1 -1 e = [yi(w(k),xi)] 2 w(k+1) = w(k) + ex; ; Example 1 sign(x)={ -1 : learning rate f(w(k),x;) = sign(w(k), w (5) = x > 0 x 0 Done! xi + w(k)) [0.4, 0, -0.2]
Step by Step Solution
3.38 Rating (170 Votes )
There are 3 Steps involved in it
Based on the information provided it appears that you are attempting to train a perceptron mo... View full answer

Get step-by-step solutions from verified subject matter experts


