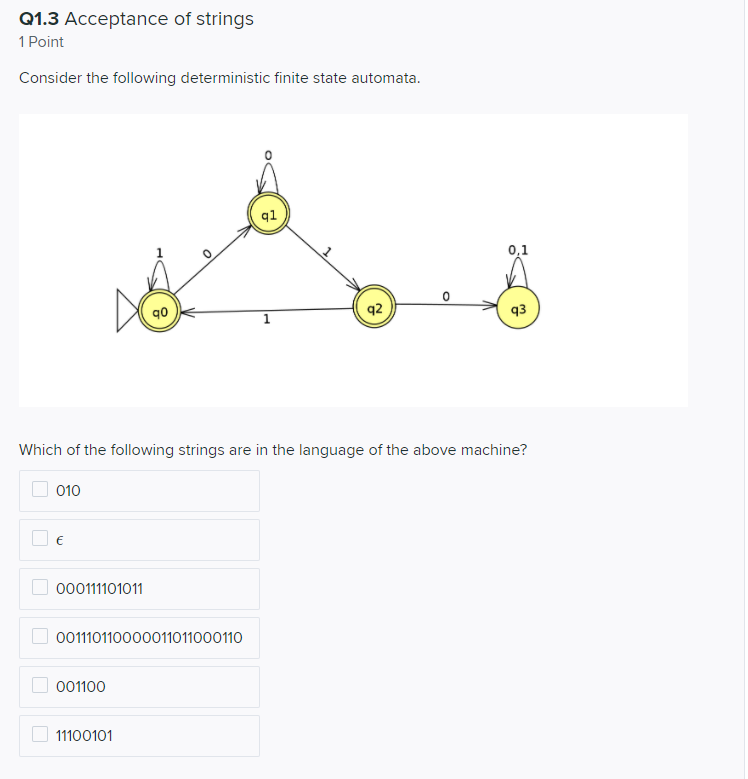
Q1 Finite State Automata 7 Points The following questions concern both deterministic and non-deterministic finite state automata. Q1.1 Finite state machine basics 1 Point From the following statements select all that are true. The alphabet of a finite state machine is finite. A finite state machine must have an accepting state. A finite state machine may have more than one start state. The empty sting (e) is accepted by every finite state machine. A finite state machine may either accept, reject or decline a string. A finite state machine accepts a string when the machine transitions to an accepting state. A finite state machine will terminate on every input. Q1.3 Acceptance of strings 1 Point Consider the following deterministic finite state automata. 91 0,1 90 92 93 Which of the following strings are in the language of the above machine? 010 000111101011 001110110000011011000110 001100 11100101 Q1.4 Non-deterministic finite state machine basics 1 Point Which of the follow statements about non-deterministic finite state automata are true? A deterministic finite state automata is a non-deterministic finite state automata. For every non-deterministic finite state automata there exists a deterministic finite state automata that is equivalent. The codomain of the transition function is the powerset of the set of states. The set of accepting states maybe empty. A non-deterministic finite automata accepts a string if and only if every computation terminates in an accepting state. A non-deterministic finite automata always accepts the empty string. A non-deterministic finite automata may have many initial states. Q2.1 Regular languages 1 Point Which of the following languages are regular languages? {W {0,1}* w is a palindrome} {0,1}* {w = {a,b,c}* ab is not a substring of w} {w = {0,1}* W mod 3=0} {ab a {0,1}* Ab {x,y}} {1"O" | n E N} {x|x E (AUC) 1 x B} where A, B, C are regular languages. Q2.2 Properties of regular languages 1 Point Which of the following are properties of regular languages? For every regular language there exists a non-deterministic finite state automata with 5 states that recognises it. For every regular language there exists a minimal deterministic finite state machine that recognises it. There exists a regular language such that no non-deterministic finite state machine recognises it. For every two regular languages A and B we have that {w | W E A V W E B} is regular. Regular languages are closed with respect to every binary operator. Q2.4 Pumping lemma 1 Point Which of the following statements are true. The pumping lemma applies to all regular languages. Given a regular language A, every w E A can be "pumped". Let A be a regular language and let W E A such that|w|p, where p is the pumping length. Let xyz be a division of w as described in the pumping lemma, then xz E A. Let A be a regular language and let w A such that|w| Zp, where p is the pumping length. Let xyz be a division of w as described in the pumping lemma, then xyz E A The pumping lemma proves all languages are regular