Question
Q1. From a large number of actuarial exam scores, a random sample of 375 scores is selected, and it is found that 258 of these


Q1.
From a large number of actuarial exam scores, a random sample of 375 scores is selected, and it is found that
258 of these 375 are passing scores. Based on this sample, find a 95%
confidence interval for the proportion of all scores that are passing. Then find the lower limit and upper limit of the 95% confidence interval.
Carry your intermediate computations to at least three decimal places. Round your answers to two decimal places.
|
Q2.
A union of restaurant and foodservice workers would like to estimate the mean hourly wage, ?, of foodservice workers in the U.S. The union will choose a random sample of wages and then estimate ? using the mean of the sample. What is the minimum sample size needed in order for the union to be 95% confident that its estimate is within $0.45 of ? ? Suppose that the standard deviation of wages of foodservice workers in the U.S. is about $2.10.
Carry your intermediate computations to at least three decimal places. Write your answer as a whole number (and make sure that it is the minimum whole number that satisfies the requirements).
Q3
Below are four bivariate data sets and their scatter plots. (Note that all of the scatter plots are displayed with the same scale.) Each data set is made up of sample values drawn from a population.
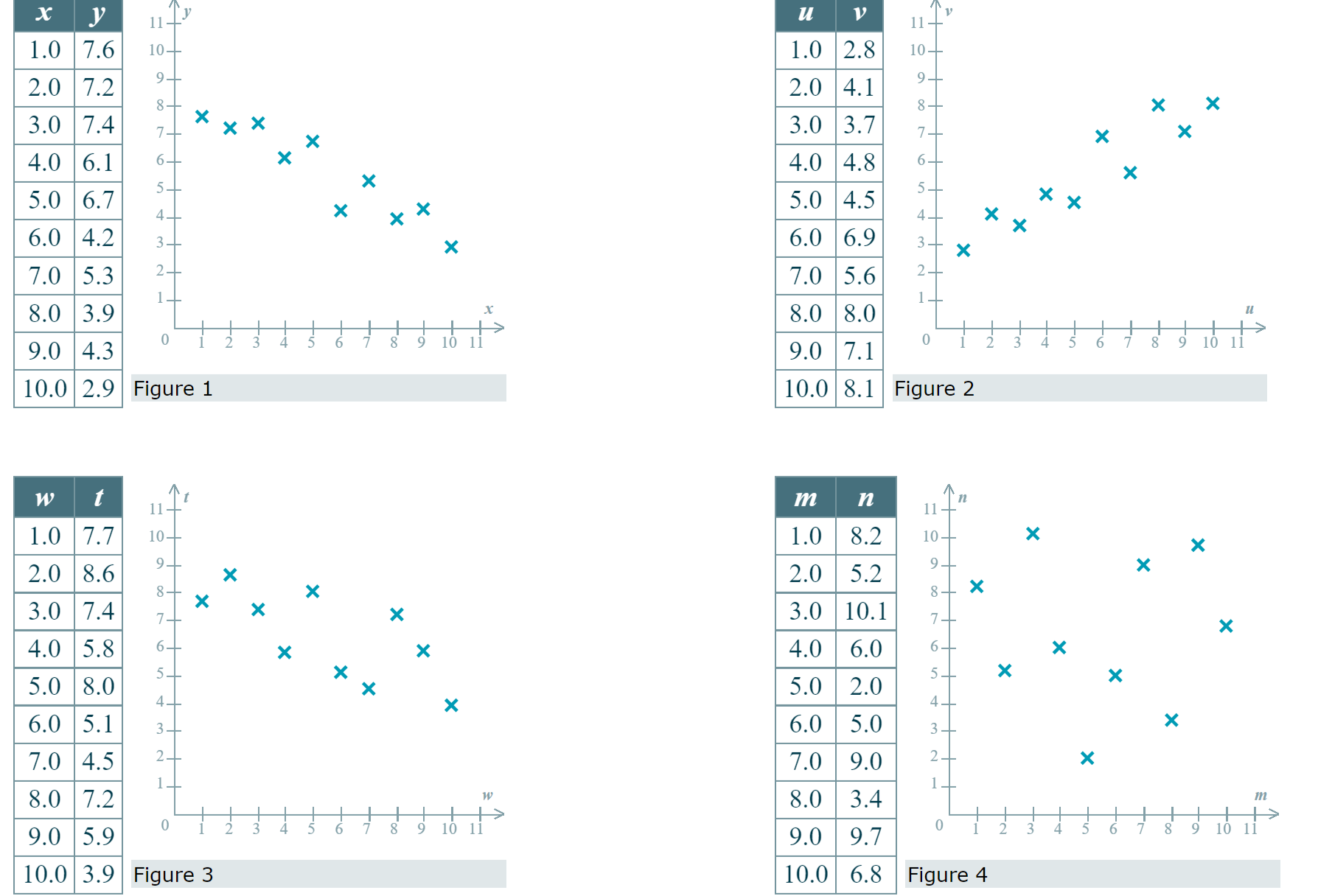
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


