Question
Q1. If Amy invests $100 in stocks at t = 1, what is the expected value of her second period wealth? Q2. If instead, she

Q1. If Amy invests $100 in stocks at t = 1, what is the expected value of her second period wealth?
Q2. If instead, she invests $100 in savings at t = 1, what is the expected value of her second period wealth?
Q3. If Amy is risk neutral, as a financial advisor, would you suggest she invest in her savings or in stocks? (Choose among the following)
(i) Invest in savings
(ii) Invest in stocks
(iii) She is indifferent between both options
Q4. As before, assume without proof that at t = 1, she still consumes $100 and invests the remaining $100.
If Amys utility function is 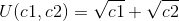 , what is Amy's lifetime expected utility from investing purely in stocks? Do not include consumption at t = 1.
, what is Amy's lifetime expected utility from investing purely in stocks? Do not include consumption at t = 1.
Q5. Assuming the same utility function in the previous question, what is Amys lifetime expected utility from investing purely in savings? Do not include consumption at t = 1.
Q6. Based on your answers to the previous two questions, what would you recommend Amy do: invest the $100 in savings or in stocks? (Choose among the following)
(i) Invest in savings
(ii) Invest in stocks
(iii) She is indifferent between both options
Amy is figuring out her budget for two periods, t 1,2. In each period, she has an income y, with y = 200 and y2 = 0.c denotes her consumption level at period t. Amy decides to spend half of her first period income immediately, so c1 = 100, and invest the other half ($100). Amy has two investment options. One option is to buy stocks from company B. Each share costs $1 at t = 1. Att = 2, the stock price is uncertain. There is a 10% chance the stock price increases to $4 per share, a 50% chance the stock price increases to $2.25 per share, and a 40 % chance the company B goes bankrupt and the stock price falls to $0 per share. Amy's other option is to invest all $100 in a savings account. But at t = 2, there is also a random shock to the savings account. There is a 50% chance the bank operates normally and the interest rate is r = 44% and a 50% chance the interest rate falls to 0 (but Amy can still get her $100 principal back). For rational answers, please enter your answers exactly (e.g. instead of 0.33). If your answer is irrational, please round to three decimal places (e.g. 3.141 for it). U(cl,c2) = vcl + c2
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


