Question
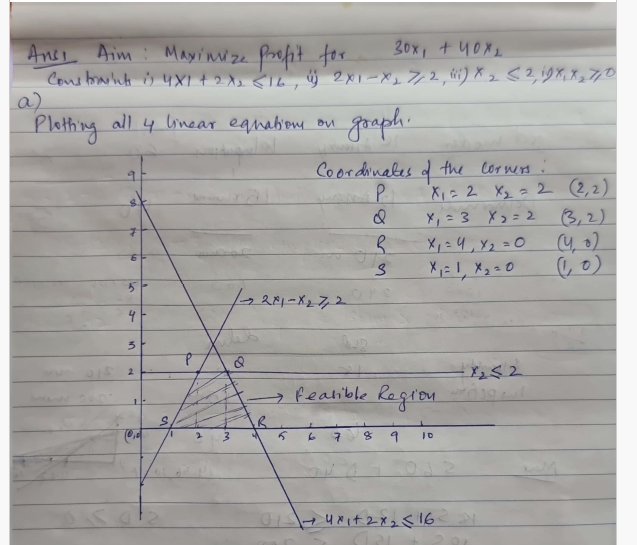
Q1. Solve the following problem, using the Corner Point Method. Maximize profit = 30x1 + 40x2 Subject to 4x1 + 2x2 ? 16 2x1 -
Q1. Solve the following problem, using the Corner Point Method. Maximize profit = 30x1 + 40x2 Subject to 4x1 + 2x2 ? 16 2x1 - x2 ? 2 x2 ? 2 x1, x2 ? 0 a) Draw lines graphically and show the feasible region and corner points on your figure. (10 Points) b) Find the optimal value of decision variables and calculate profit at the optimal point. (10 Points) c) For the optimal solution, how much slack or surplus is there for each? (5 points)
============================================================================
images q1 and q2 for the Q1
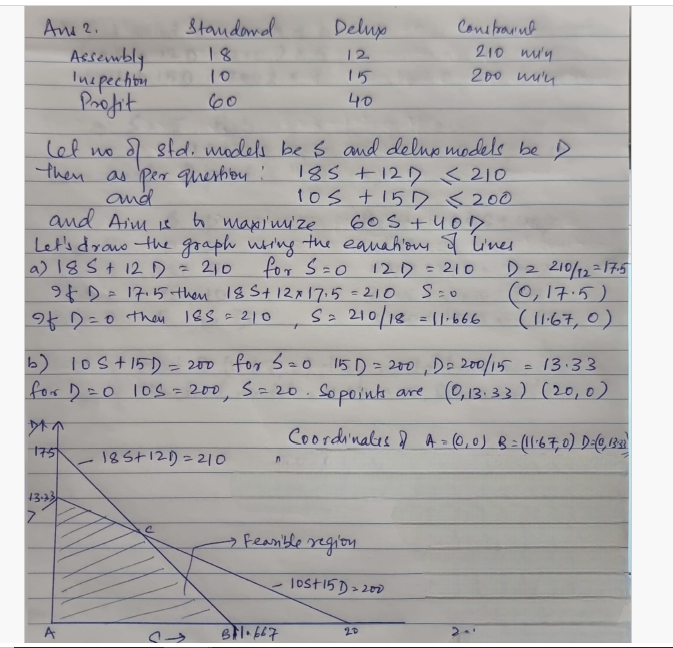
======================================================================================= Q2. Billy Penny is trying to determine how many units of two types of lawn mowers to produce each day. One of these is the Standard model, while the other is the Deluxe model. The profit per unit on the Standard model is $60, while the profit per unit on the Deluxe model is $40. The Standard model requires 18 minutes of assembly time, while the Deluxe model requires 12 minutes of assembly time. The Standard model requires 10 minutes of inspection time, while the Deluxe model requires 15 minutes of inspection time. There are 210 minutes of assembly time and 200 minutes of inspection time available each day. a) Formulate the linear programming problem. (10 Points) b) How many units of each product should be manufactured to maximize profits using the Corner Point Method or Isoprofit Line Solution Method? (15 Points)
======================================================================================


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


