Question

1 Approved Answer

Posted on Sep 25, 2024

Q3 Encode(n) Precond: 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,1) (0,1,0,1) (0,1,0,0) (0,0,1,1) (0,0,1,0) (0,0,0,1) (0,0,0,0) (0,1,1,0) +(0,0,1,1) (0,1,0,1) (0,1,1,0) +(0,1,1,0) (0,0,0,0) (0,1,1,0) - (0,1,1,0) (0,0,0,0)

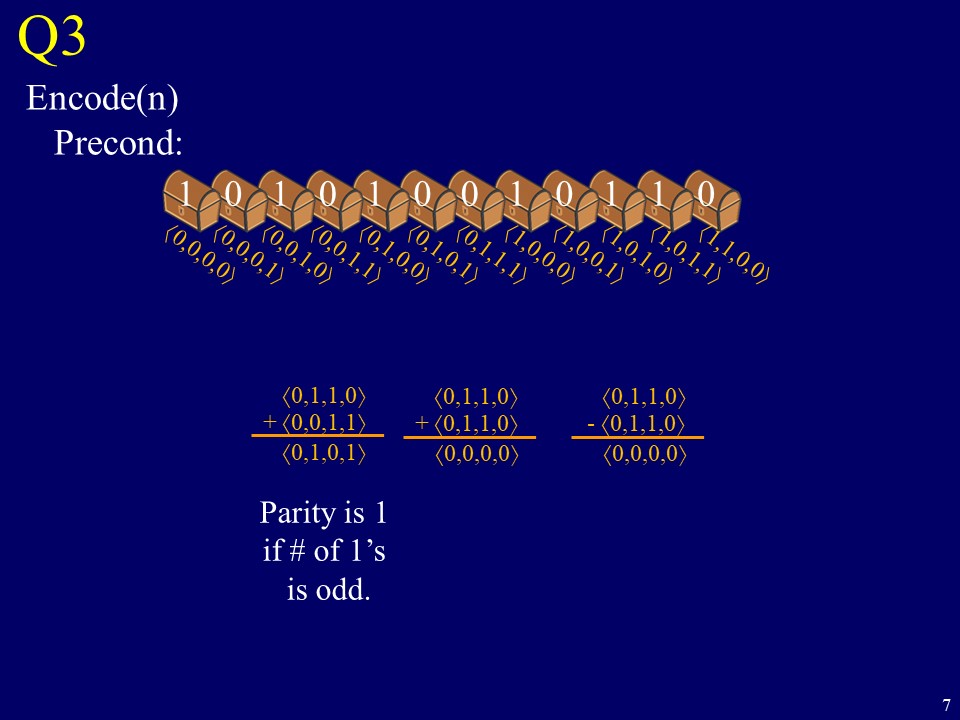
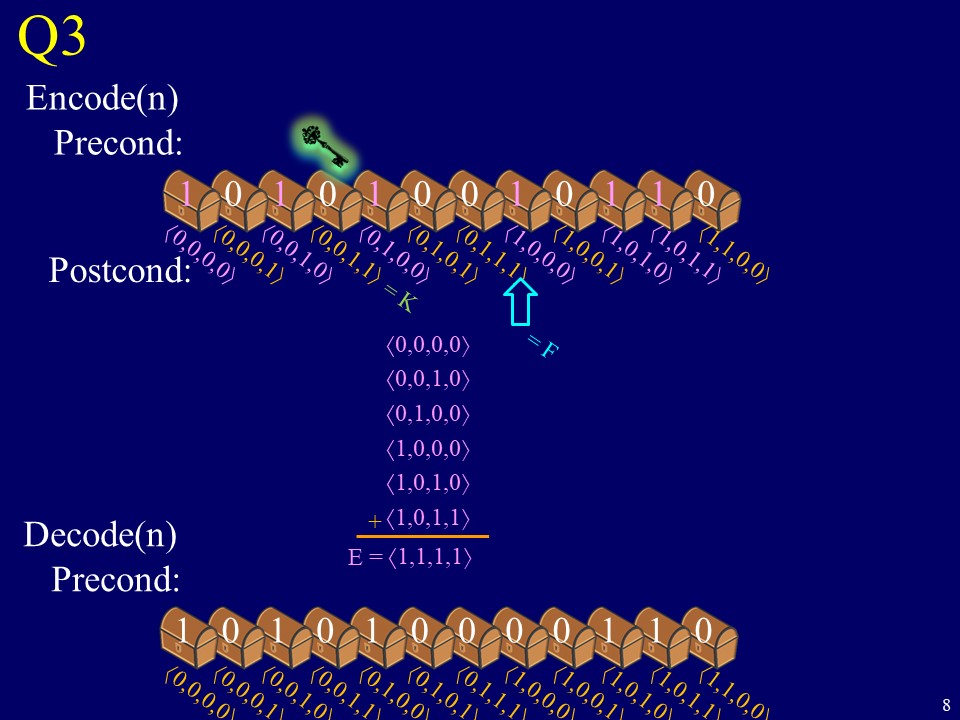
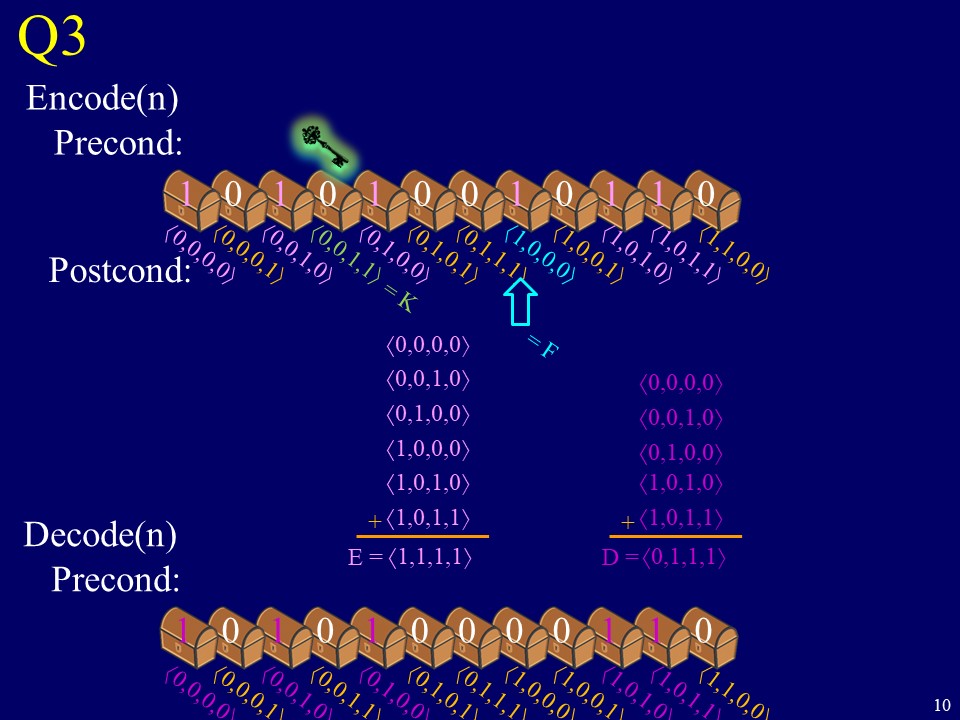
image text in transcribed

Q3 Encode(n) Precond: 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,1) (0,1,0,1) (0,1,0,0) (0,0,1,1) (0,0,1,0) (0,0,0,1) (0,0,0,0) (0,1,1,0) +(0,0,1,1) (0,1,0,1) (0,1,1,0) +(0,1,1,0) (0,0,0,0) (0,1,1,0) - (0,1,1,0) (0,0,0,0) Parity is 1 if # of ls is odd. 7 0 D) K Q3 Encode(n) Precond: Postcond: (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,0,0) (1,0,1,0) +(1,0,1,1) Decode(n) E =(1,1,1,1) Precond: 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,11 (0,1,0,1) = F (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,1,0,0\ (1,0,1,1 (1,0,1,0 (1,0,0,11 (1,0,0,01 (0,1,1,1 (0,1,0,1 (0,1,0,01 (0,0,1,1 (0,0,1,0 (0,0,0,1 (0,0,0,01 1 0 1 0 1 0 0 0 0 1 1 0 8 8 (a) Now each box has a vector name, a bit label given by the warden (one of which is flipped by encoder(n)), and maybe contains the key. Both encoder(n) and decoder(n) will add up the vectors of the boxes that have label 1. Let E and D denote these sums. Let F denote the vector name of the box whose bit encoder(n) flips. Give an equation giving D as a function of E and F. (b) Let K denote the vector name of the box containing the key. Give a simple equation with which decoder(n) will determine K from D. (c) Given this, give an equation with which encoder(n) will determine F from E and K. (d) Characterize the values of n for which your algorithm works and for which it does not. Explain why. See next slide 9 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,11 (0,1,0,1) e 0 D) K Q3 Encode(n) Precond: Postcond: (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,0,0) (1,0,1,0) +(1,0,1,1) Decode(n) E =(1,1,1,1) Precond: = F (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,1,0,01 (1,0,1,1) (1,0,1,0 (1,0,0,11 (1,0,0,01 (0,1,1,1 (0,1,0,1 (0,1,0,0 (0,0,1,1 (0,0,1,0 (0,0,0,1 (0,0,0,0" (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,1,0) + (1,0,1,1) D=(0,1,1,1) 0 0 0 07 10 Q3 Encode(n) Precond: 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,1) (0,1,0,1) (0,1,0,0) (0,0,1,1) (0,0,1,0) (0,0,0,1) (0,0,0,0) (0,1,1,0) +(0,0,1,1) (0,1,0,1) (0,1,1,0) +(0,1,1,0) (0,0,0,0) (0,1,1,0) - (0,1,1,0) (0,0,0,0) Parity is 1 if # of ls is odd. 7 0 D) K Q3 Encode(n) Precond: Postcond: (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,0,0) (1,0,1,0) +(1,0,1,1) Decode(n) E =(1,1,1,1) Precond: 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,11 (0,1,0,1) = F (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,1,0,0\ (1,0,1,1 (1,0,1,0 (1,0,0,11 (1,0,0,01 (0,1,1,1 (0,1,0,1 (0,1,0,01 (0,0,1,1 (0,0,1,0 (0,0,0,1 (0,0,0,01 1 0 1 0 1 0 0 0 0 1 1 0 8 8 (a) Now each box has a vector name, a bit label given by the warden (one of which is flipped by encoder(n)), and maybe contains the key. Both encoder(n) and decoder(n) will add up the vectors of the boxes that have label 1. Let E and D denote these sums. Let F denote the vector name of the box whose bit encoder(n) flips. Give an equation giving D as a function of E and F. (b) Let K denote the vector name of the box containing the key. Give a simple equation with which decoder(n) will determine K from D. (c) Given this, give an equation with which encoder(n) will determine F from E and K. (d) Characterize the values of n for which your algorithm works and for which it does not. Explain why. See next slide 9 71,1,0,0) 71,0,1,1) 071,0,1,0) 71,0,0,1) 71,0,0,0) (0,1,1,11 (0,1,0,1) e 0 D) K Q3 Encode(n) Precond: Postcond: (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,0,0) (1,0,1,0) +(1,0,1,1) Decode(n) E =(1,1,1,1) Precond: = F (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,1,0,01 (1,0,1,1) (1,0,1,0 (1,0,0,11 (1,0,0,01 (0,1,1,1 (0,1,0,1 (0,1,0,0 (0,0,1,1 (0,0,1,0 (0,0,0,1 (0,0,0,0" (0,0,0,0) (0,0,1,0) (0,1,0,0) (1,0,1,0) + (1,0,1,1) D=(0,1,1,1) 0 0 0 07 10