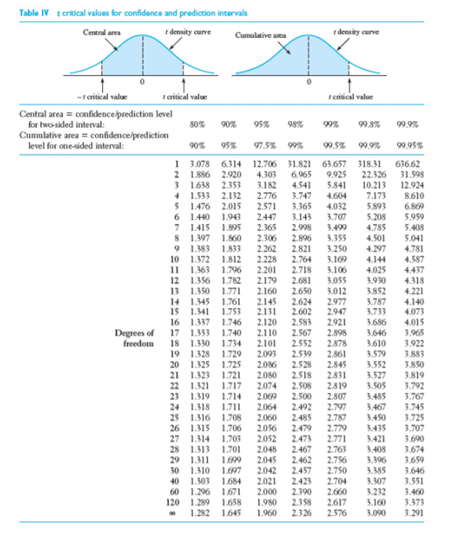
Q3: The weight of a particular device depends on the machine producing that. Suppose Sample I is a random sample of 10 devices produced by Machine A and Sample II is a random sample of 16 devices produced by Machine B. Let x, and s, denote the sample mean and the sample standard deviation of devices in Sample i where i = I or II. Suppose X1 = 290, S = 12 XII = 321, SII = 22 A) Calculate a two-sided 95% confidence interval for the difference between the true mean weight of devices produced by Machine A and the true mean weight of devices produced by Machine B. [25 points] B) Based on the interval, does it appear plausible that the true mean weight of devices produced by Machine B exceeds the true mean weight of devices produced by Machine A? Why? [10 points]Table IV : critical values for confidence and prediction intervals Central area F density carve Cumulative area / deming curve -I critical value F critical value F annical value Central area = confidence/prediction level for two-sided Interval: Cumulative area = confidence/prediction level for one-sided interval: 95 97 5 90%% 99.9% 99.95 3.078 6.314 12.706 31.821 63.657 318.31 636.62 1.896 2.920 4.303 6.965 9.925 LWNE 22.326 31.598 1.638 2.353 3.182 4.541 5.841 10.213 12 924 1.533 2.132 2.776 3.747 4.604 7.173 8.610 5 1.476 2.015 2.571 3.365 4.032 5.893 6.869 6 1.440 1.943 2.4:47 3.143 3.707 5.208 5.959 7 1.415 1.895 2.365 3,499 4.785 5.404 1.397 1.860 2.306 2 896 3.355 4.501 5.041 1.383 1.833 2.262 2.821 3.250 4.797 4.781 10 1.372 1,812 2.228 2.764 3.169 4144 4.587 11 1.363 1.796 2.201 2.718 3.106 4.025 4.437 12 1.356 1.782 2.179 2.681 3.055 3.930 4.318 13 1.350 1.771 2.160 2.650 3.012 3.852 4.121 14 1.345 1.761 2.145 2634 2.977 3.787 4.140 15 1.341 1.753 2.131 2.601 2.0-47 4.737 4.071 16 1.317 1.746 2.120 2.583 2.921 3.686 4.015 Degrees of 17 1.333 1.740 2.1 10 2.567 2.898 3.646 3.905 freedom 18 1.330 1.734 2.101 2.552 2.878 3.610 3.922 19 1.328 1.729 2.093 2.530 2.861 3.579 3.853 20 1.325 1.725 2.056 2.528 2.845 3.552 3.850 21 1.323 1.721 2.080 2.518 2.831 3.527 3.819 22 1.321 1.717 2.074 2.508 2.819 3.505 3.792 23 1.319 1.714 2069 2 500 2.8:07 3.485 3.767 24 1.318 1.711 2064 2491 2.797 3.467 3.745 25 1.316 1.708 2.060 2485 2.787 3.450 3.725 26 1.315 1.706 2.056 2.479 2.779 3.435 3.707 27 1.314 1.703 2.052 2473 2.771 3.421 3.690 28 1.313 1.701 2.0-48 2.467 2.763 3.409 3.674 29 1.311 1.697 2.045 2461 2.756 3.906 3.659 30 1.310 1.697 2042 2.457 2.750 3.646 40 1.303 1.684 2.021 2.423 2.704 3.307 3.551 60 1.296 1.671 2.000 2.390 1.660 3.732 3.460 120 1.209 1.658 1.930 2.358 2.617 3.160 3.373 1.281 1.645 1.960 2326 2.576 3.090 3.291