quantum engineering

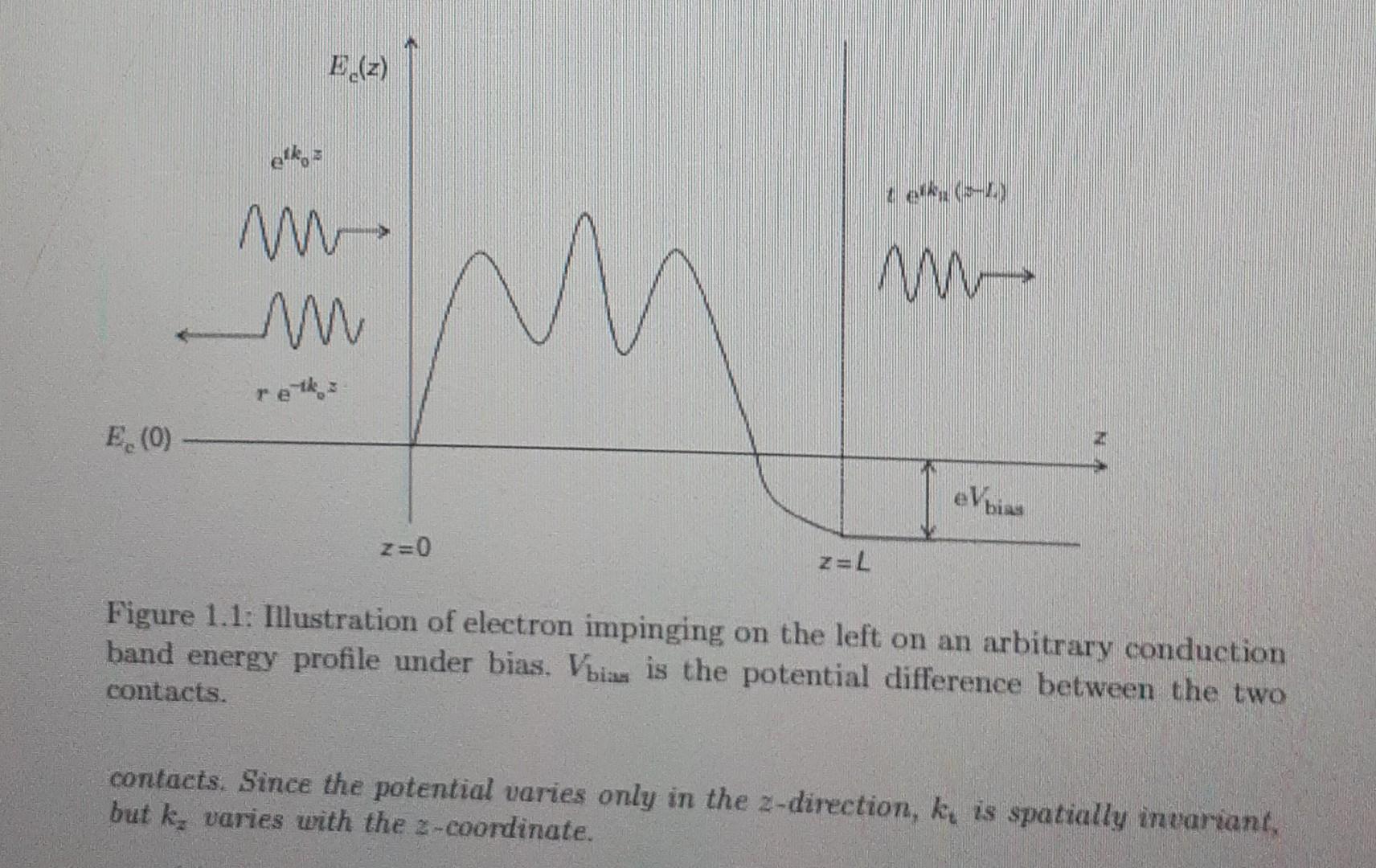
(a) Consider an electron in a solid, which could be a semiconductor or an insulator. We will exclude a metal since the potential inside a metal is usually spatially invariant as a metal cannot sustain an electric field. The potential that an electron sees inside a semiconductor or insulator is the conduction band profile. We will assume that it is time independent and varies only along one direction, which we call the 2-direction (see Figure 1.1). The effective mass also varies along that direction. Show that the stationary solutions of the Schrdinger equation obey the equation t? d h2 2m*(z) | dr? var, y, z) 1 d m*(z) dz V(2. y. 2) dy? + Ec(z)v(r, y, z) = Ev(r, y, z), (1.1) where Ec(z) is the conduction band edge and E is the total energy of the electron, which is independent of 2 because the total energy is a good quantum number in the absence of dissipation. In Equation (1.1). E = Ekin(-) + E-(-) and Ekin (z) = (K?(z) +13) 2m: (1.2) where k, and kt k+ k are the longitudinal and transverse components of the electron's wave vector, respectively, while m = m*(0) is the effective mass in the E.(z) elke M M - E.(0) eVbiss Z=0 Figure 1.1: Illustration of electron impinging on the left on an arbitrary conduction band energy profile under bias. Vbian is the potential difference between the two contacts. contacts. Since the potential varies only in the 2-direction, ky is spatially invariant, but k, varies with the 2-coordinate