QUESTION 1:
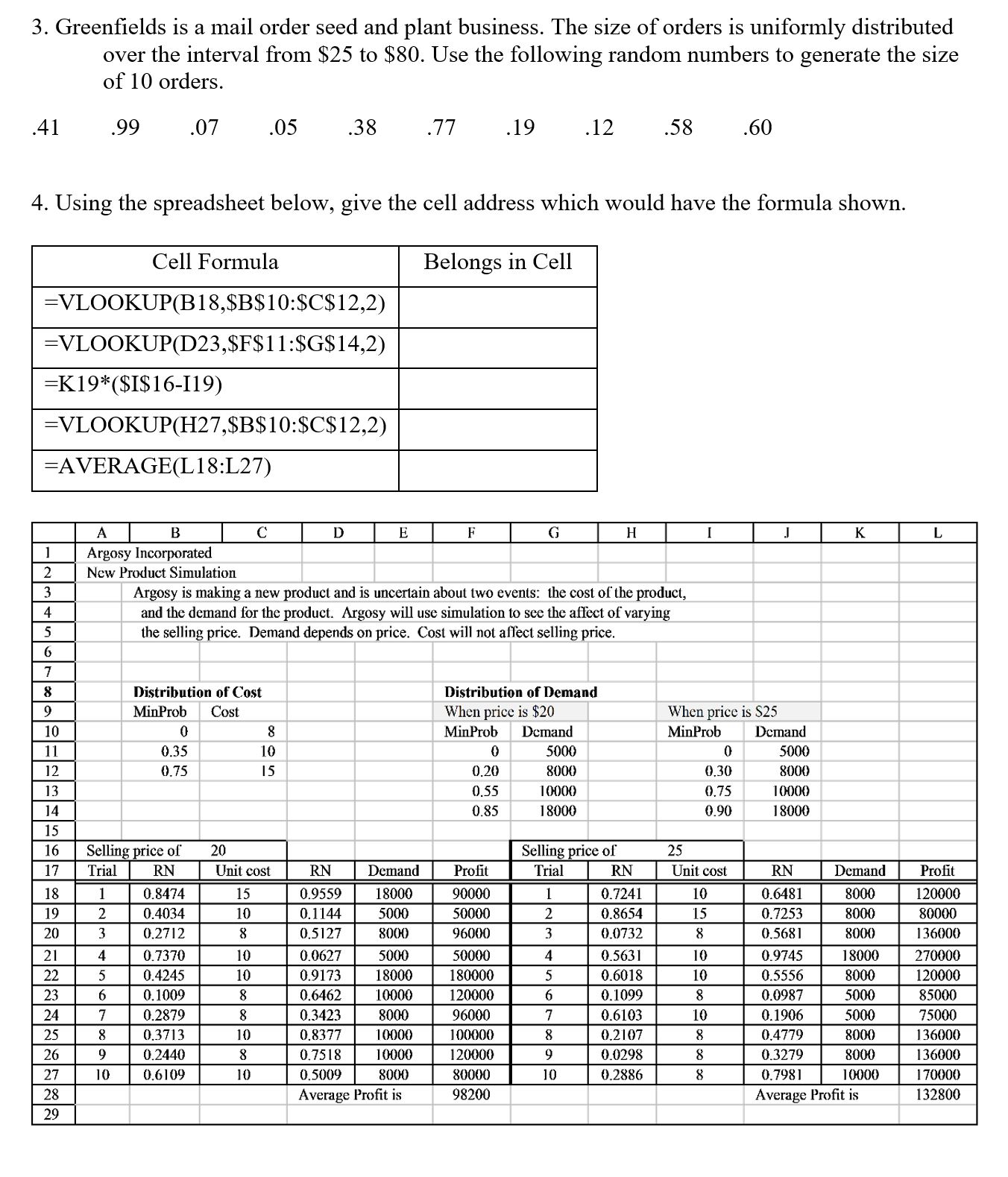
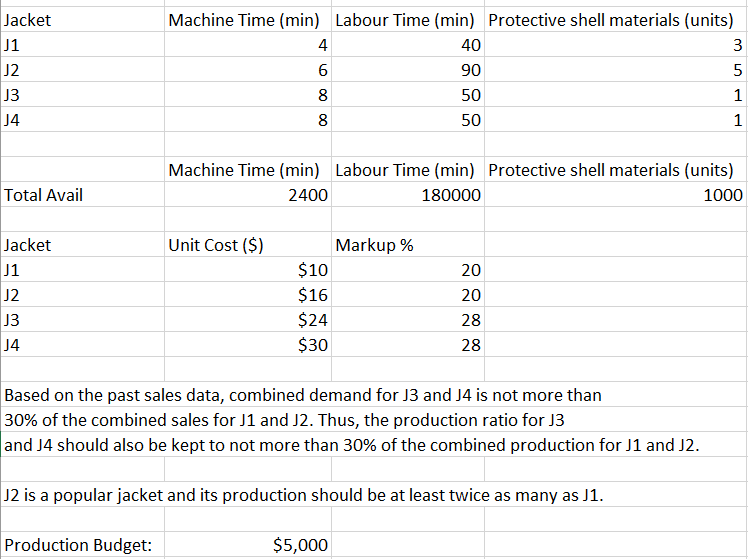
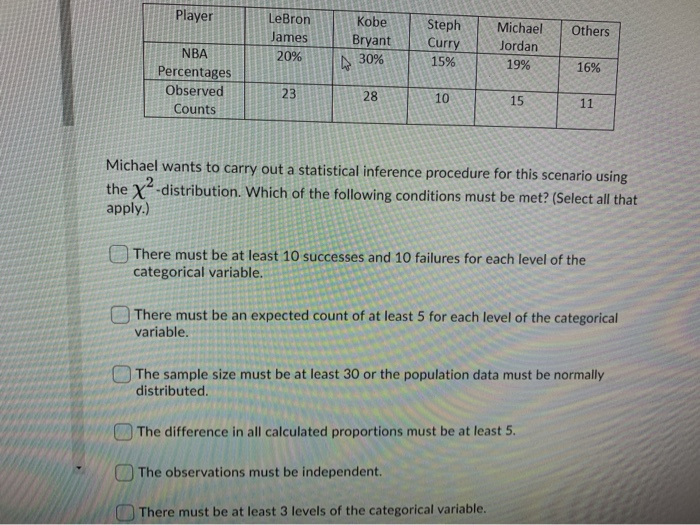
3. Greenfields is a mail order seed and plant business. The size of orders is uniformly distributed over the interval from $25 to $80. Use the following random numbers to generate the size of 10 orders. 41 .99 07 .05 38 .77 .19 .12 .58 .60 4. Using the spreadsheet below, give the cell address which would have the formula shown. Cell Formula Belongs in Cell =VLOOKUP(B18,$B$10:$C$12,2) =VLOOKUP(D23,$F$11:$G$14,2) =K19*($I$16-119) =VLOOKUP(H27,$B$10:$C$12,2) =AVERAGE(L 18:L27) A B C D E F G H I J K L Argosy Incorporated N N New Product Simulation Argosy is making a new product and is uncertain about two events: the cost of the product, and the demand for the product. Argosy will use simulation to see the affect of varying the selling price. Demand depends on price. Cost will not affect selling price. Distribution of Cost Distribution of Demand MinProb Cost When price is $20 10 When price is $25 0 MinProb Demand MinProb Demand 0.35 10 5000 5000 12 0.75 15 0.20 8000 0.30 8000 0.55 10000 0.75 14 10000 0.85 18000 0.90 18000 15 16 Selling price of 20 Selling price of 25 17 Trial RN Unit cost RN Demand Profi Trial RN Unit cost RN Demand Profit 18 0.8474 15 0.9559 18000 90000 0.7241 19 10 0.6481 0.4034 8000 120000 10 0.1144 5000 50000 0.8654 20 15 0.7253 8000 0.2712 80000 0.5127 3000 6000 0.0732 0.5681 8000 136000 21 0.7370 0.0627 5000 0000 22 0.5631 10 0.9745 8000 0.4245 270000 0.9173 8000 80000 23 0.6018 10 6 0.1009 0.5556 3000 20000 0.6462 0000 20000 6 0.1099 24 0.2879 0.0987 000 35000 0.3423 3000 96000 0.6103 10 0.1906 5000 25 0.3713 75000 0.8377 10000 100900 0.2107 26 0.4779 8000 136000 0.2440 0.7518 10000 120000 27 10 0.0298 10 0.3279 8000 0.6109 136000 0.5009 8000 80000 10 0.2886 g 28 0.7981 10000 170000 Average Profit is 98200 29 Average Profit is 132800Jacket Machine Time (min) Labour Time (min) Protective shell materials (units) 4 40 J2 6 90 13 8 50 14 8 50 Machine Time (min) Labour Time (min) Protective shell materials (units) Total Avail 2400 180000 1000 Jacket Unit Cost ($) Markup % J1 $10 20 J2 $16 20 J3 $24 28 14 $30 28 Based on the past sales data, combined demand for J3 and J4 is not more than 30% of the combined sales for J1 and J2. Thus, the production ratio for J3 and J4 should also be kept to not more than 30% of the combined production for J1 and J2. J2 is a popular jacket and its production should be at least twice as many as J1. Production Budget: $5,000Player LeBron Kobe Steph Michael Others James Bryant Curry Jordan NBA 20% 30% 15% 19% 16% Percentages Observed 23 28 10 15 11 Counts Michael wants to carry out a statistical inference procedure for this scenario using the X"-distribution. Which of the following conditions must be met? (Select all that apply.) There must be at least 10 successes and 10 failures for each level of the categorical variable. There must be an expected count of at least 5 for each level of the categorical variable. The sample size must be at least 30 or the population data must be normally distributed. The difference in all calculated proportions must be at least 5. The observations must be independent. There must be at least 3 levels of the categorical variable.Simulation - Discrete Event 1. For the past 50 days, daily sales of laundry detergent in a large grocery store have been recorded (to the nearest 10). Units Sold Number of Times 30 OC 40 12 50 15 60 10 70 5 a. Determine the relative frequency for each number of units sold. b. Suppose that the following random numbers were obtained using Excel: 12 .96 .53 .80 .95 .10 .40 .45 .77 .29 c. Use these random numbers to simulate 10 days of sales. 2. The drying rate in an industrial process is dependent on many factors and varies according to the following distribution. Minutes Relative Frequency 14 30 a UI A U 27 18 .11 . Compute the mean drying time. b. Using these random numbers, simulate the drying time for 12 processes. 33 .09 .19 .81 .12 .88 .53 .95 .77 .61 91 .47 c. What is the average drying time for the 12 processes you simulated