Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Question 1 (40 marks) A new hamburger outlet is unsure of the best price to sell its burgers for maximum profit. To gather data


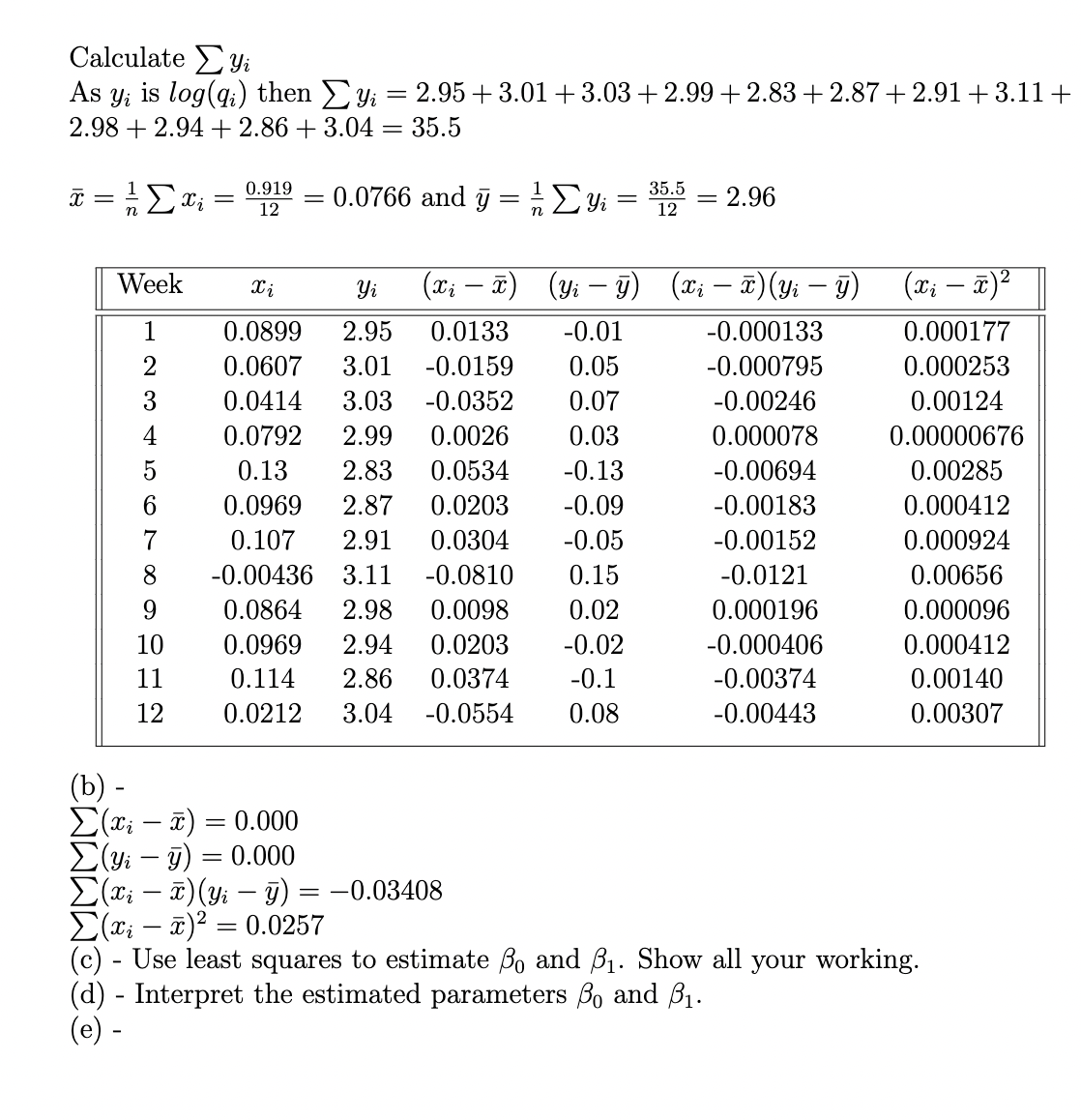
Question 1 (40 marks) A new hamburger outlet is unsure of the best price to sell its burgers for maximum profit. To gather data on what the optimal price should be, each week they change the hamburger price slightly using "special deals" of various kinds. The quantities sold and the corresponding prices are shown in the table below. Note that you need to use the natural logarithm for this question. Week Number of Hamburgers Sold (q;) Price (pi) 1 892 1.23 2 1012 1.15 3 1060 1.10 4 987 1.20 5 680 1.35 6 739 1.25 Download 7 809 1.28 8 1275 0.99 9 946 1.22 10 874 1.25 11 720 1.30 12 1096 1.05 (a) (4 marks) Assume the statistical model is given by: Yi = Bo+Bxi + i, where y = log (qi), xi = log (pi), and ei ~ N (0, 2). Calculate x; and Yi. What are the sample means x and y. Compute all the elements in the table below to three significant figures. Week Xi Yi (xi Yi (Xi x) (Yi F) (xi - x) 1 9 10 11 12 -23456782222 (b) (4 marks) Calculate (x; - x), (Yi T), (xi x) (yi ), and (xi x). (c) (4 marks) Use least squares to estimate o and 1. Show all your working. (d) (4 marks) Interpret the estimated parameters o and . (e) (4 marks) Use the least squares estimates from part (c) to compute the fitted values of y for each value of x in the sample, and complete the table below to three significant figures. Week xi Yi i i 1 Download 23456789012 11 (f) (2 marks) Estimate the standard deviation of the errors, o. (g) (4 marks) Find a 95% confidence interval for and interpret the result. (h) (4 marks) Test the hypotheses that Ho: = 0 and H B 0 using a = 0.05 and interpret the result. (i) (4 marks) Predict the quantity of hamburgers purchased when the price of one hamburger is $1.25, construct a prediction interval and interpret the results. Note that the formula for computing the prediction interval in a simple linear regression is: 1 Var (o)=2(1+ N + (x0 ) Var (31) (j) (6 marks) Construct a 95% confidence interval for (31 - Bo). Calculate As Yi Yi is log(q) then y = 2.95 +3.01 +3.03 +2.99 +2.83 +2.87+2.91 +3.11+ 2.982.94 + 2.86 +3.04 = 35.5 x = n - = 0.919 12 = 0.0766 and y = n Yi = 355 = 2.96 Week Xi Yi - (xi x) (Yi ) (xi x)(Yi ) (2 x) 1 0.0899 2.95 0.0133 -0.01 -0.000133 0.000177 0.0607 3.01 -0.0159 0.05 -0.000795 0.000253 0.0414 3.03 -0.0352 0.07 -0.00246 0.00124 0.0792 2.99 0.0026 0.03 0.000078 0.00000676 0.13 2.83 0.0969 2.87 0.0203 0.0534 -0.13 -0.00694 0.00285 -0.09 -0.00183 0.000412 0.107 2.91 0.0304 -0.05 -0.00152 0.000924 8 -0.00436 3.11 -0.0810 0.15 -0.0121 0.00656 9 0.0864 2.98 0.0098 0.02 0.000196 0.000096 10 0.0969 2.94 0.0203 -0.02 -0.000406 0.000412 11 0.114 2.86 0.0374 -0.1 -0.00374 0.00140 12 0.0212 3.04 -0.0554 0.08 -0.00443 0.00307 (b). (xx)=0.000 (yi )=0.000 = -0.03408 C(xi - x) (yi ) = - (x)=0.0257 - (c) Use least squares to estimate Bo and B. Show all your working. (d) Interpret the estimated parameters Bo and . - (e) -
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


