Question #1:

a) In Excel, enter 20 columns of random numbers (using =RANDBETWEEN(1,30)). Within each column, randomly select n = 5 numbers. You should now have 20 columns of 5 numbers each. The numbers should be between 1 and 30. Calculate the average of each column (20 averages). Calculate the center (mean) and spread (standard deviation) of the 20 averages.

b) Enter an additional set of 20 columns of random numbers (again using =RANDBETWEEN(1,30)). Within each column, randomly select n = 50 numbers. You should now have 20 columns of 50 numbers each. The numbers should be between 1 and 30. Calculate the average of each column (20 averages). Calculate the center (mean) and spread (standard deviation) of the 20 averages.

c) Comment on any differences in center and spread between n = 5 and n = 50. Were these differences (or lack thereof) expected? Explain.

Question #2: State the null hypothesis 0 and the alternative hypothesis in each case:

a) A national study reports that households spend an average of 35% of their food expenditures in restaurants. A restaurant association in your area wonders if the national finding applies locally. They interview a sample of 60 households and ask about the total food budget and the amount spent in restaurants.

b) Experiments on learning in animals sometimes measure how long it takes a mouse to find its way through a maze. The mean time is 21.4 seconds across many national studies. A researcher thinks that playing classical music will cause the mice to complete the maze configuration more slowly. She measures how long each of 16 mice takes with the classical music as a stimulus, then compares this result to the national average.

c) A dual x-ray absorptiometry scanner is used to measure bone mineral density for people who may be at risk for osteoporosis. To be sure that the scanner measurements are accurate, an object called a "phantom" that has known mineral density = 1.35 grams per square centimeter is measured. This phantom is scanned 8 times.

Question 3: A test of the null hypothesis 0: = 0 gives test statistic z = 1.45.

a) What is the P-value if the alternative is : > 0?

b) What is the P-value if the alternative is :

c) What is the P-value if the alternative is : = 0?

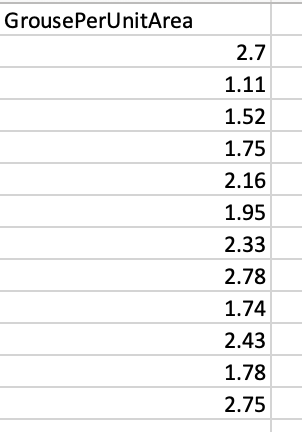
Question #4 Grouse density was determined to be 2.5 grouse per unit area in 2003 for a particular management area (based on intensive, expert observation at the time). The file grouse.csv contains a sample of 12 observations of grouse density for the same area in 2013.

a) Build and report a qq Plot of the 2013 observations. Note that Student's-t based confidence intervals appear appropriate to use in this case. Thus, find 80%, 90%, and 95% confidence intervals for the true mean grouse per unit area in 2013.

b) Write down the null and alternative hypotheses for testing whether grouse density changed between 2003 and 2013. Use the 2013 data and a Student's-t statistic to test your null hypothesis. What is the P-value for the test statistic given the alternative hypothesis? Would you, personally, reject or fail to reject the null hypothesis? Why?