Question
Question 1. A traveler wants to walk a road of a given distance n. There is a cafe on his/her road placed in every discrete
Question 1. A traveler wants to walk a road of a given distance n. There is a cafe on his/her road placed in every discrete location i {1, 2, , n}. The traveler has to rest and have a coffee at some of these cafe locations all of them having have changing coffee prices depending on the distance he has walked since the last location he rested.
The prices for all possible distances are stored in a price array. That is, price[1] denotes the price that the traveler has to pay for the coffee if s/he walked a distance of 1 since the last location s/he rested, price[2] denotes the price that he has to pay if s/he walked a distance of 2 since the last location s/he rested and so on. For example; when n = 9, if s/he firstly rests at location 3, s/he has to pay price[3] and then, if s/he rests at location 5, s/he has to pay price[2] and then, if s/he rests at location 9, s/he has to pay price[4]. Hence, the total price makes price[3] + price[2] + price[4]. Your goal is to minimize the total price s/he has to pay.
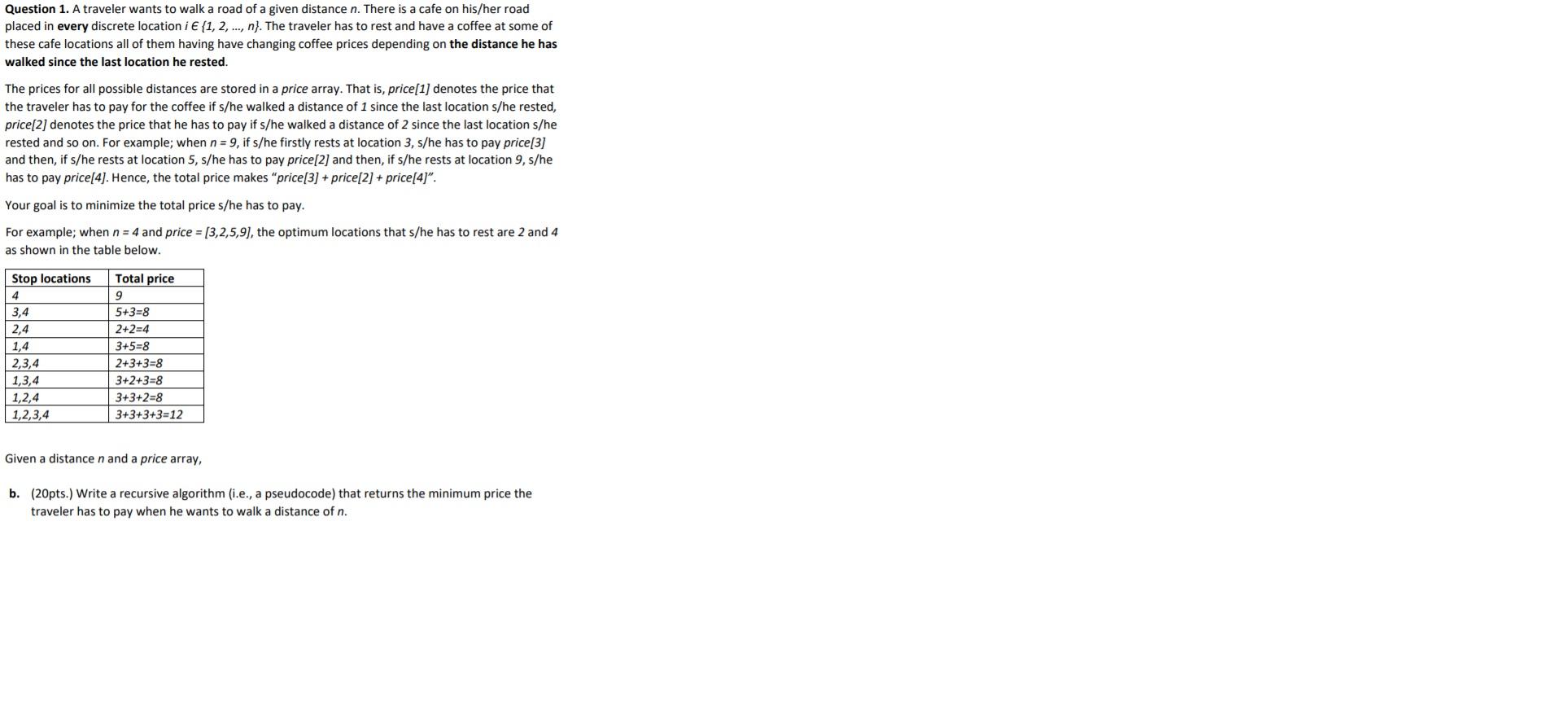
For example; when n = 4 and price = [3,2,5,9], the optimum locations that s/he has to rest are 2 and 4 as shown in the table below.
b. Write a recursive algorithm (i.e., a pseudocode) that returns the minimum price the traveler has to pay when he wants to walk a distance of n.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


