Question
Question 1 Interpreting Confidence Intervals: If theheights of men and women from the associated data files(MBODY & FBODY-found in the Lab 11 file) are used
Question 1
Interpreting Confidence Intervals:If theheights of men and women from the associated data files(MBODY & FBODY-found in the Lab 11 file) are used to construct a 95% confidence interval for the
difference between the two population means, the result is 11.61 cm
Express the confidenceinterval with the heights of women being population1 and the heights of men being population 2. Choose the correct confidence interval below.
Group of answer choices
17.32
-17.32
-11.61
11.61
Question 2
IQ and Lead Exposure.The data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below.
Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of people
with high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 21,x= 86.90476,s= 8.988352
Are the samples in this case independent meaning we should use a 2-sample Independent T-Test or are they dependent samples meaning we should use a Matched Pairs Design?
Group of answer choices
Independent so 2-Sample Independent Design
Dependent so a Matched Pairs Design
Question 3
IQ and Lead Exposure: Step 1The data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below.
Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of people
with high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 21,x= 86.90476,s= 8.988352
Fill in the blanks to complete Step 1: The hypotheses:
H012= [ Select ] ["57", "-57", "0", "50"]
H112 [ Select ] ["greater than", "less than", "not equal to"] [ Select ] ["57", "-57", "0", "50"]
where1isthe mean from the low lead level group and2is the mean from the high lead level group
Question 4
IQ and Lead Exposure: Step 3 Checking the RequirementsThe data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics are for these groups are summarized below.
Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 33,x= 86.90476,s= 8.988352
For each of the requirements necessary for this test, choose the correct answer indetermining if the are met or not.
1.) The population standarddeviations are not equal.
This requirement is met. We can use the sample standard deviations to help gauge if the population standard deviations are equal. True/False [ Select ] ["True", "False"]
2.) The samples are independent. True/False [ Select ] ["True", "False"]
3.) Both samples are random samples True/False [ Select ] ["True", "False"]
4.) The sample sizes are both larger than 30. True/False [ Select ] ["True", "False"]
Question 5
IQ and Lead Exposure: Step 4 CalculationsThe data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics are for these groups are summarized below. Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 33,x= 86.90476,s= 8.988352
1: Find the value of the test statistic and p-value following the instructions below:
a) Press STAT & scroll to TESTS & select "2-SampTTest..." (option 4 in TI83Plus) & press Enter (for a hypothesis test of a claim involving two populations
b) Enter the following:
- Inpt: Stats (The statistics are given above)
- x1= sample mean from the low lead level group
- Sx1=sample standard deviation from the low lead level group
- n1 =sample size from the low lead level group
- x2= sample mean from the high lead level group
- Sx2 =sample standard deviation from the high lead level group
- n2 =sample size from the high lead level group
- Choose thecorrect direction of the alternative
- Pooled: Choose NO
c) Highlight "Calculate" and press ENTER & make note of the calculations as you will needthem below.
Enter the value of the T-Test statistic. Round to two decimal places if necessary.
T = _________?
Question 6
IQ and Lead Exposure: Step 4 CalculationsThe data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below. Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 33,x= 86.90476,s= 8.988352
1: Find the value of the test statistic and p-value following the instructions below:
a) Press STAT & scroll to TESTS & select "2-SampTTest..." (option 4 in TI83Plus) & press Enter (for a hypothesis test of a claim involving two populations
b) Enter the following:
- Inpt: Stats (The statistics are given above)
- x1= sample mean from the low lead level group
- Sx1=sample standard deviation from the low lead level group
- n1 =sample size from the low lead level group
- x2= sample mean from the high lead level group
- Sx2 =sample standard deviation from the high lead level group
- n2 =sample size from the high lead level group
- Choose thecorrect direction of the alternative
- Pooled: Choose NO
c) Highlight "Calculate" and press ENTER & make note of the calculations as you will needthem below.
Enter the value of the P-Value. Round to three decimal places if necessary.
P-value = __________?
Question 7
IQ and Lead Exposure: Step 4 ConclusionsThe data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below. Use a 0.05 significance level to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 33,x= 86.90476,s= 8.988352
Based on the T-score and the p-value, fill in the blanksbelow to draw the conclusion:
Since the p-value is [ Select ] ["greater than", "less than"] the significancelevel of 0.05, we would [ Select ] ["reject", "fail to reject"] the null hypothesis. This would mean that there [ Select ] ["is", "is not"] asignificant difference in IQ scores between people with low lead levels and high lead levels.
Question 8
IQ and Lead Exposure: Confidence IntervalThe data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below. Build a 95% Confidence interval to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Low Lead Level: n= 78, x= 92.88462,s= 15.34451
High Lead Level:n= 33,x= 86.90476,s= 8.988352
2: Find the 95% confidence interval
a) Press STAT & scroll to TESTS & select "2-SampTInt..." (option 0 in TI83Plus) & press Enter (for a hypothesis test of a claim involving two populations
b) Enter the following:
- Inpt: Stats (The statistics are given above)
- x1= sample mean from the low lead level group
- Sx1=sample standard deviation from the low lead level group
- n1 =sample size from the low lead level group
- x2= sample mean from the high lead level group
- Sx2 =sample standard deviation from the high lead level group
- n2 =sample size from the high lead level group
- Pooled: Choose NO
c) Highlight "Calculate" and press ENTER & make note of the calculations as you will needthem below.
Enter the values of the confidence interval below here. Round each value to two decimal places.
The 95% confidence interval = (_____, _____? )
Question 9
IQ and Lead Exposure: Confidence Interval (cont)The data set IQLEAD (found in the lab description) lists full IQ scores for arandom sample of subjects selected from a group with low lead levels in their blood and another random sample of subjects selected from a group withhigh lead levels in their blood. The statistics for these groups are summarized below. Build a 95% Confidence interval to test theclaim that the mean IQ score of people with low lead levels is higher than the mean IQ score of peoplewith high lead levels.
Fill in the blanksbelowto interpret the confidence interval.
"Based on this sample, we are [ Select ] ["95", "5", "1", "99"] % confident that the true difference in population mean IQ scores betweenthe low lead group and the high lead group is between 1.34 and 10.62posts. Since [ Select ] ["0", "5", "-5"] is [ Select ] ["in", "not in"] in the interval, the sample evidence indicates a difference in IQ scores between the two groups.
Question 10
Do Men and Women Have the SameMean Body TemperatureConsider the sample of bodytemperatures (F) listed in the last column of the file BODYTEMP.
The summarystatistics are given in the table below. Use a 0.01 significance level to test the claim that men and women
have different mean body temperatures. Body temperatures are given in degreesFahrenheit.
Men: n= 15, x= 98.38,s= 0.45
Women: n= 91,x= 98.17,s= 0.65
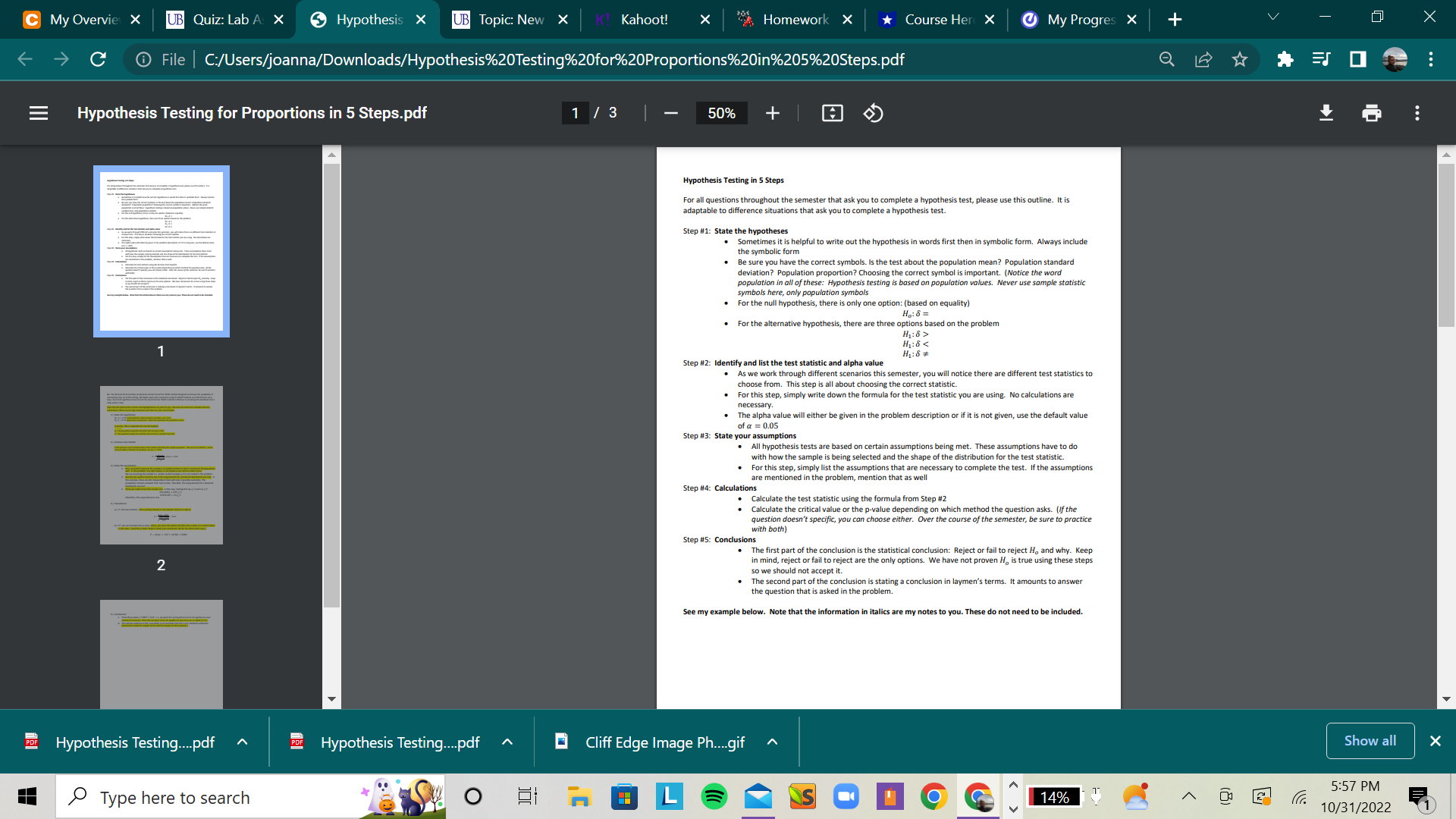
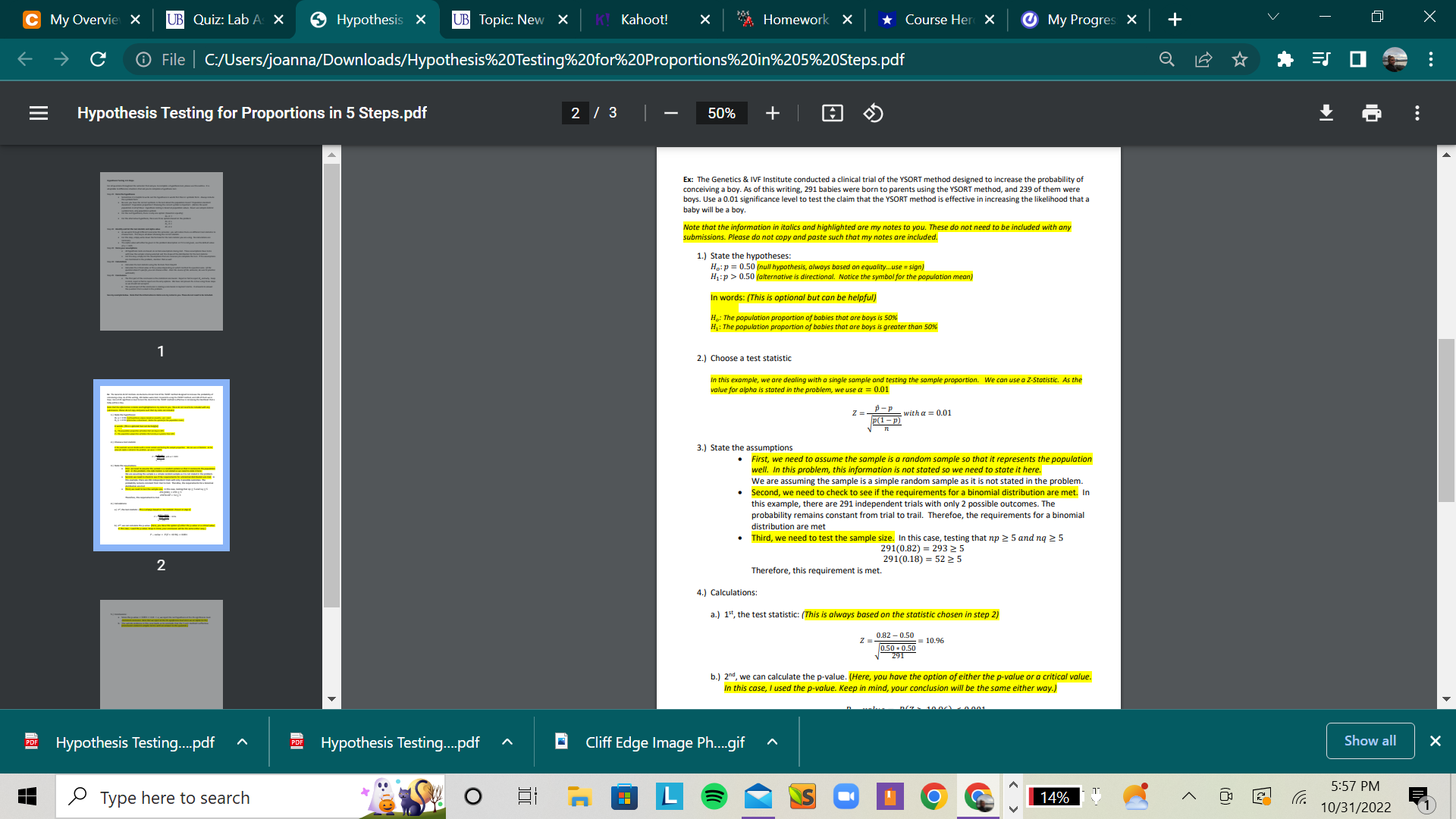
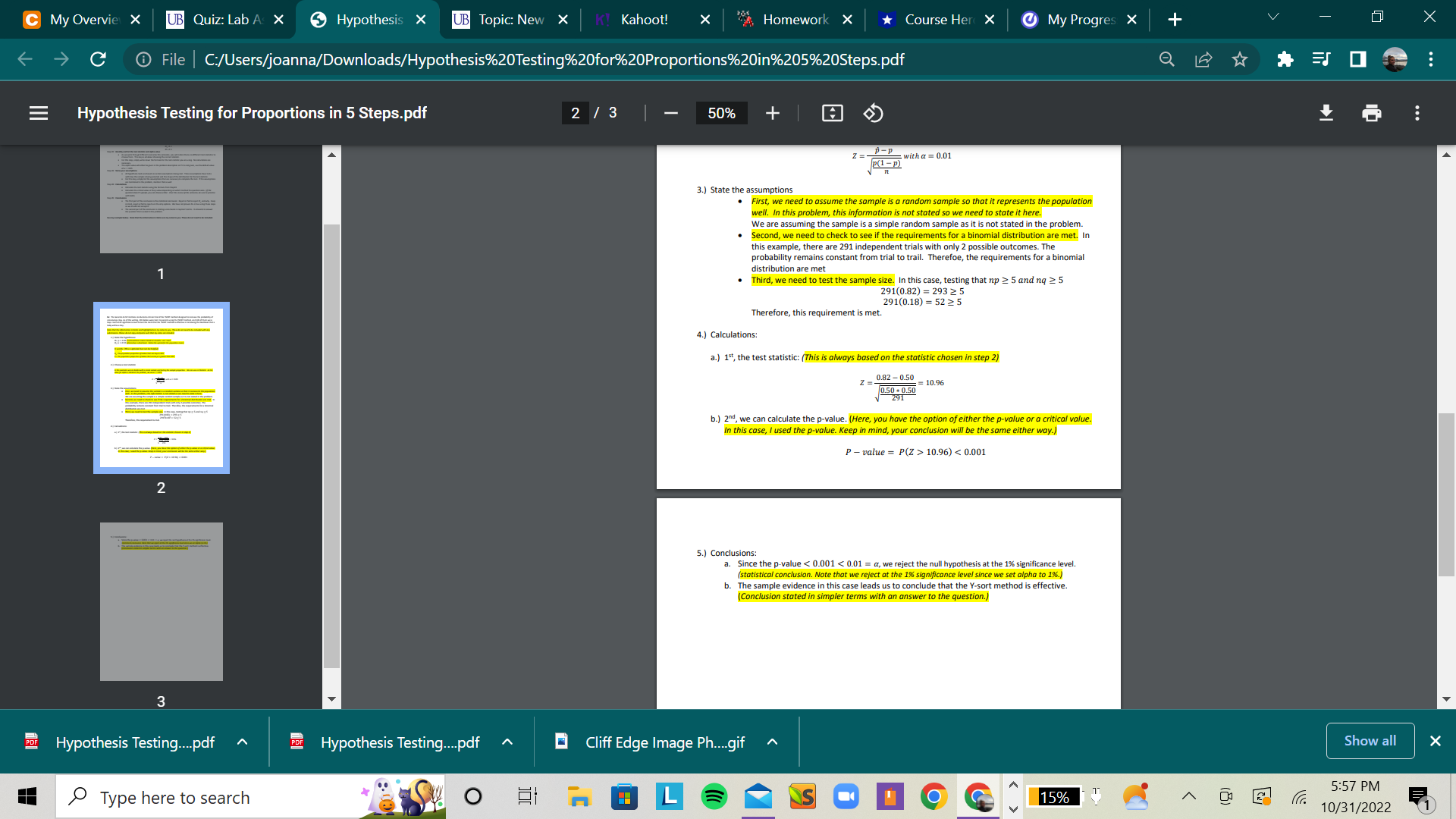
Upload work demonstrating all 5 completed steps for the hypothesis test. The 5 steps should match the steps in the example posted in the example here: Hypothesis Testing in 5 Steps.pdfDownload Hypothesis Testing in 5 Steps.pdf
Use the first 9 questions of this lab as a guide. Full credit will only be given for a completed test with all 5 steps. For step number 2, write in words: "T-Test statistic for 2 independent samples" or copy the statistics from the Powerpoint.
Female Body Temperatures
| AGE | PULSE | SYS | DIAS | HDL | LDL | WHITE | RED | PLATE | WT | HT | WAIST | ARMC | BMI |
| 60 | 78 | 122 | 60 | 74 | 140 | 9.6 | 4.70 | 317 | 59.3 | 163.7 | 82.3 | 27.5 | 22.13 |
| 24 | 80 | 120 | 64 | 56 | 142 | 7.1 | 4.64 | 224 | 74.5 | 165.5 | 88.5 | 30.0 | 27.20 |
| 49 | 68 | 90 | 48 | 70 | 72 | 7.5 | 4.61 | 248 | 77.7 | 163.1 | 94.9 | 34.4 | 29.21 |
| 62 | 56 | 150 | 80 | 40 | 164 | 6.8 | 4.09 | 309 | 97.9 | 166.3 | 111.8 | 38.7 | 35.40 |
| 53 | 76 | 132 | 58 | 67 | 109 | 5.6 | 4.36 | 335 | 71.7 | 163.6 | 86.5 | 32.2 | 26.79 |
| 18 | 78 | 88 | 52 | 96 | 93 | 5.4 | 4.64 | 278 | 60.9 | 170.9 | 78.4 | 26.7 | 20.85 |
| 41 | 78 | 100 | 60 | 43 | 122 | 6.7 | 4.98 | 312 | 60.5 | 153.5 | 81.7 | 30.5 | 25.68 |
| 21 | 90 | 114 | 72 | 80 | 116 | 8.6 | 3.76 | 338 | 88.2 | 155.7 | 111.2 | 36.9 | 36.38 |
| 21 | 96 | 94 | 54 | 77 | 84 | 10.2 | 4.30 | 290 | 43.8 | 153.0 | 79.2 | 23.2 | 18.71 |
| 19 | 60 | 100 | 54 | 41 | 55 | 4.1 | 4.66 | 236 | 47.9 | 157.0 | 63.4 | 22.6 | 19.43 |
| 19 | 98 | 110 | 74 | 23 | 115 | 13.0 | 5.66 | 310 | 126.6 | 163.7 | 103.8 | 40.5 | 47.24 |
| 58 | 66 | 188 | 0 | 76 | 98 | 9.2 | 4.71 | 460 | 64.8 | 161.3 | 90.4 | 29.0 | 24.91 |
| 44 | 100 | 106 | 74 | 39 | 139 | 5.9 | 4.81 | 317 | 75.6 | 168.6 | 93.6 | 32.1 | 26.60 |
| 52 | 76 | 130 | 76 | 52 | 122 | 8.0 | 4.95 | 304 | 81.0 | 156.4 | 111.8 | 32.8 | 33.11 |
| 48 | 64 | 126 | 76 | 38 | 100 | 7.0 | 4.32 | 239 | 72.8 | 159.4 | 97.2 | 31.9 | 28.65 |
| 36 | 82 | 90 | 56 | 37 | 99 | 9.1 | 4.35 | 243 | 67.3 | 164.2 | 83.9 | 30.8 | 24.96 |
| 48 | 62 | 168 | 90 | 57 | 131 | 5.7 | 3.93 | 351 | 58.0 | 169.0 | 80.3 | 26.7 | 20.31 |
| 34 | 72 | 110 | 66 | 81 | 59 | 4.6 | 4.69 | 242 | 107.8 | 161.6 | 120.6 | 40.7 | 41.28 |
| 22 | 78 | 98 | 60 | 37 | 90 | 6.0 | 4.66 | 217 | 54.1 | 161.1 | 80.5 | 25.2 | 20.85 |
| 61 | 74 | 112 | 70 | 50 | 130 | 5.7 | 5.26 | 173 | 59.6 | 150.8 | 97.1 | 29.7 | 26.21 |
| 21 | 90 | 116 | 66 | 73 | 144 | 8.9 | 4.23 | 228 | 48.9 | 166.6 | 79.7 | 21.6 | 17.62 |
| 33 | 90 | 128 | 72 | 61 | 84 | 6.4 | 4.81 | 259 | 115.7 | 175.7 | 119.9 | 39.9 | 37.48 |
| 32 | 68 | 116 | 72 | 33 | 112 | 8.1 | 4.50 | 193 | 75.3 | 169.0 | 96.3 | 32.0 | 26.36 |
| 37 | 72 | 112 | 66 | 41 | 128 | 7.9 | 4.36 | 417 | 114.9 | 160.5 | 124.4 | 43.2 | 44.60 |
| 19 | 82 | 126 | 60 | 60 | 107 | 4.4 | 4.68 | 193 | 60.0 | 159.1 | 74.5 | 29.4 | 23.70 |
| 51 | 72 | 94 | 60 | 62 | 209 | 4.9 | 4.64 | 244 | 67.3 | 166.7 | 83.8 | 31.0 | 24.22 |
| 35 | 78 | 120 | 78 | 67 | 77 | 5.3 | 4.01 | 266 | 77.3 | 151.5 | 94.0 | 37.2 | 33.68 |
| 18 | 104 | 94 | 32 | 79 | 39 | 5.3 | 4.11 | 286 | 49.7 | 156.2 | 71.2 | 24.2 | 20.37 |
| 60 | 62 | 120 | 76 | 64 | 85 | 4.7 | 4.37 | 206 | 58.4 | 148.7 | 90.7 | 30.0 | 26.41 |
| 58 | 72 | 148 | 62 | 44 | 162 | 9.8 | 4.66 | 426 | 82.2 | 168.3 | 103.6 | 33.4 | 29.02 |
| 60 | 72 | 126 | 76 | 42 | 111 | 5.3 | 4.89 | 244 | 79.5 | 159.6 | 98.3 | 36.4 | 31.21 |
| 48 | 88 | 126 | 72 | 41 | 104 | 4.9 | 4.35 | 295 | 80.3 | 165.9 | 96.6 | 33.0 | 29.18 |
| 31 | 74 | 112 | 72 | 44 | 192 | 6.3 | 4.56 | 282 | 56.4 | 147.6 | 79.1 | 29.5 | 25.89 |
| 29 | 72 | 120 | 78 | 57 | 110 | 5.4 | 5.10 | 211 | 64.3 | 165.4 | 85.7 | 31.0 | 23.50 |
| 46 | 82 | 110 | 76 | 69 | 123 | 7.0 | 5.30 | 355 | 102.1 | 159.8 | 119.6 | 39.5 | 39.98 |
| 18 | 78 | 98 | 66 | 60 | 70 | 13.5 | 4.83 | 357 | 62.3 | 158.5 | 83.2 | 30.6 | 24.80 |
| 50 | 78 | 130 | 72 | 47 | 155 | 10.0 | 4.65 | 272 | 74.6 | 165.6 | 97.5 | 31.0 | 27.20 |
| 20 | 98 | 114 | 54 | 67 | 108 | 10.3 | 4.29 | 251 | 116.3 | 164.9 | 140.0 | 35.5 | 42.77 |
| 56 | 72 | 174 | 86 | 55 | 158 | 5.1 | 4.40 | 219 | 92.6 | 172.0 | 109.0 | 39.0 | 31.30 |
| 18 | 64 | 108 | 58 | 82 | 50 | 6.6 | 4.26 | 234 | 65.0 | 170.2 | 81.8 | 27.5 | 22.44 |
Male Body Temperatures
| AGE | PULSE | SYS | DIAS | HDL | LDL | WHITE | RED | PLATE | WT | HT | WAIST | ARMC | BMI |
| 18 | 60 | 132 | 68 | 44 | 213 | 8.7 | 4.91 | 409 | 64.4 | 178.8 | 81.4 | 28.4 | 20.14 |
| 20 | 74 | 120 | 68 | 41 | 88 | 5.9 | 5.59 | 187 | 61.8 | 177.5 | 74.8 | 26.8 | 19.62 |
| 43 | 86 | 106 | 84 | 71 | 174 | 7.3 | 4.44 | 250 | 78.5 | 187.8 | 84.1 | 32.3 | 22.26 |
| 39 | 54 | 104 | 60 | 41 | 121 | 6.2 | 4.80 | 273 | 86.3 | 172.4 | 95.5 | 39.0 | 29.04 |
| 60 | 90 | 122 | 80 | 57 | 124 | 5.9 | 5.17 | 278 | 73.1 | 181.7 | 90.1 | 29.4 | 22.14 |
| 18 | 80 | 122 | 62 | 50 | 99 | 6.4 | 5.24 | 279 | 58.5 | 169.0 | 69.8 | 28.7 | 20.48 |
| 57 | 66 | 126 | 78 | 60 | 114 | 3.9 | 4.51 | 237 | 134.3 | 186.9 | 137.8 | 42.8 | 38.45 |
| 27 | 68 | 118 | 60 | 47 | 122 | 6.4 | 4.77 | 200 | 79.8 | 183.1 | 94.4 | 32.0 | 23.80 |
| 20 | 68 | 110 | 40 | 44 | 112 | 9.8 | 5.02 | 209 | 64.8 | 176.4 | 74.2 | 29.2 | 20.82 |
| 18 | 56 | 96 | 56 | 33 | 67 | 4.0 | 5.10 | 203 | 58.1 | 183.4 | 69.9 | 26.2 | 17.27 |
| 63 | 80 | 114 | 76 | 48 | 108 | 3.8 | 4.45 | 206 | 76.1 | 169.6 | 95.2 | 32.0 | 26.46 |
| 20 | 62 | 128 | 78 | 46 | 94 | 5.6 | 5.41 | 174 | 118.4 | 185.4 | 117.5 | 39.9 | 34.45 |
| 24 | 74 | 108 | 76 | 62 | 69 | 6.6 | 5.45 | 219 | 56.2 | 166.1 | 77.0 | 26.2 | 20.37 |
| 46 | 60 | 126 | 78 | 45 | 77 | 4.9 | 4.27 | 302 | 73.4 | 169.3 | 90.5 | 33.1 | 25.61 |
| 29 | 52 | 116 | 82 | 43 | 120 | 9.6 | 4.90 | 285 | 126.9 | 193.5 | 122.0 | 37.9 | 33.89 |
| 63 | 60 | 138 | 76 | 39 | 84 | 8.6 | 4.60 | 254 | 84.4 | 173.1 | 104.0 | 32.2 | 28.17 |
| 21 | 66 | 110 | 50 | 41 | 86 | 5.2 | 4.93 | 195 | 97.8 | 171.6 | 104.1 | 37.9 | 33.21 |
| 45 | 64 | 144 | 84 | 47 | 77 | 9.2 | 4.28 | 290 | 66.5 | 180.8 | 76.4 | 29.9 | 20.34 |
| 40 | 64 | 112 | 70 | 46 | 201 | 6.6 | 4.74 | 240 | 90.5 | 175.3 | 98.6 | 37.0 | 29.45 |
| 50 | 46 | 130 | 74 | 56 | 196 | 3.2 | 4.98 | 270 | 83.7 | 178.3 | 89.7 | 36.0 | 26.33 |
| 48 | 68 | 136 | 82 | 38 | 179 | 6.9 | 5.20 | 264 | 88.7 | 172.8 | 102.1 | 33.7 | 29.71 |
| 64 | 58 | 146 | 70 | 37 | 140 | 7.1 | 5.17 | 208 | 80.4 | 165.2 | 104.6 | 32.6 | 29.46 |
| 18 | 68 | 106 | 62 | 61 | 117 | 6.9 | 4.85 | 271 | 64.0 | 176.6 | 77.6 | 26.1 | 20.52 |
| 50 | 70 | 136 | 76 | 41 | 117 | 7.0 | 5.77 | 386 | 65.7 | 174.2 | 87.5 | 30.2 | 21.65 |
| 20 | 56 | 122 | 86 | 56 | 87 | 8.4 | 5.09 | 203 | 58.9 | 181.7 | 69.1 | 25.1 | 17.84 |
| 20 | 66 | 112 | 80 | 59 | 78 | 5.9 | 5.24 | 223 | 82.4 | 176.0 | 83.4 | 36.0 | 26.60 |
| 47 | 78 | 128 | 90 | 40 | 159 | 5.1 | 5.18 | 261 | 85.1 | 173.7 | 96.1 | 33.2 | 28.21 |
| 19 | 68 | 114 | 56 | 54 | 113 | 10.0 | 5.34 | 282 | 87.7 | 177.1 | 97.2 | 35.3 | 27.96 |
| 55 | 62 | 100 | 68 | 40 | 155 | 4.4 | 4.89 | 184 | 111.9 | 174.5 | 122.4 | 36.5 | 36.75 |
| 23 | 70 | 106 | 78 | 75 | 85 | 7.1 | 5.59 | 204 | 70.9 | 180.4 | 81.5 | 31.0 | 21.79 |
| 21 | 72 | 134 | 78 | 55 | 90 | 7.9 | 5.94 | 287 | 101.8 | 177.3 | 97.5 | 38.8 | 32.38 |
| 19 | 74 | 128 | 68 | 48 | 104 | 8.1 | 5.39 | 219 | 99.0 | 172.5 | 106.7 | 36.4 | 33.27 |
| 64 | 64 | 108 | 80 | 50 | 154 | 5.6 | 5.24 | 257 | 100.5 | 180.2 | 109.6 | 36.9 | 30.95 |
| 30 | 50 | 106 | 68 | 57 | 114 | 4.1 | 4.72 | 206 | 78.9 | 172.7 | 91.8 | 33.2 | 26.45 |
| 43 | 70 | 112 | 68 | 38 | 156 | 9.5 | 5.34 | 342 | 79.2 | 168.6 | 96.7 | 34.0 | 27.86 |
| 23 | 58 | 120 | 68 | 78 | 103 | 4.9 | 5.23 | 319 | 86.1 | 178.3 | 86.6 | 38.2 | 27.08 |
| 64 | 60 | 140 | 62 | 45 | 145 | 8.9 | 4.98 | 251 | 100.8 | 176.7 | 118.1 | 36.0 | 32.28 |
| 40 | 88 | 98 | 56 | 82 | 135 | 11.0 | 5.06 | 178 | 76.4 | 174.8 | 81.5 | 34.7 | 25.00 |
| 23 | 84 | 126 | 68 | 44 | 123 | 8.6 | 5.64 | 220 | 77.4 | 172.1 | 92.1 | 31.9 | 26.13 |
| 44 | 76 | 154 | 86 | 51 | 170 | 6.9 | 5.47 | 268 | 89.7 | 173.4 | 103.3 | 37.5 | 29.83 |
IQLEAD
| LEAD | AGE | SEX | YEAR1 | YEAR2 | IQV | IQP | IQF |
| 1 | 11 | 1 | 25 | 18 | 61 | 85 | 70 |
| 1 | 9 | 1 | 31 | 28 | 82 | 90 | 85 |
| 1 | 11 | 1 | 30 | 29 | 70 | 107 | 86 |
| 1 | 6 | 1 | 29 | 30 | 72 | 85 | 76 |
| 1 | 11 | 1 | 2 | 34 | 72 | 100 | 84 |
| 1 | 6 | 1 | 29 | 25 | 95 | 97 | 96 |
| 1 | 6 | 1 | 25 | 24 | 89 | 101 | 94 |
| 1 | 15 | 2 | 24 | 15 | 57 | 64 | 56 |
| 1 | 7 | 2 | 24 | 16 | 116 | 111 | 115 |
| 1 | 7 | 1 | 31 | 24 | 95 | 100 | 97 |
| 1 | 13 | 2 | 21 | 19 | 82 | 76 | 77 |
| 1 | 10 | 2 | 29 | 27 | 116 | 136 | 128 |
| 1 | 12 | 1 | 32 | 29 | 99 | 100 | 99 |
| 1 | 12 | 1 | 36 | 32 | 74 | 90 | 80 |
| 1 | 15 | 1 | 30 | 25 | 100 | 135 | 118 |
| 1 | 10 | 1 | 29 | 23 | 72 | 104 | 86 |
| 1 | 15 | 1 | 28 | 28 | 126 | 149 | 141 |
| 1 | 9 | 2 | 28 | 19 | 80 | 99 | 88 |
| 1 | 8 | 1 | 34 | 22 | 86 | 107 | 96 |
| 1 | 11 | 1 | 21 | 22 | 94 | 99 | 96 |
| 1 | 7 | 1 | 35 | 27 | 100 | 113 | 107 |
| 1 | 11 | 2 | 39 | 38 | 72 | 104 | 86 |
| 1 | 6 | 1 | 36 | 31 | 63 | 101 | 80 |
| 1 | 6 | 1 | 19 | 25 | 101 | 111 | 107 |
| 1 | 9 | 1 | 29 | 24 | 85 | 118 | 101 |
| 1 | 13 | 2 | 1 | 24 | 85 | 99 | 91 |
| 1 | 9 | 2 | 22 | 20 | 124 | 122 | 125 |
| 1 | 6 | 1 | 23 | 18 | 105 | 87 | 96 |
| 1 | 13 | 1 | 21 | 18 | 81 | 118 | 99 |
| 1 | 6 | 1 | 32 | 26 | 87 | 113 | 99 |
| 1 | 12 | 2 | 26 | 27 | 100 | 128 | 115 |
| 1 | 8 | 2 | 20 | 24 | 91 | 121 | 106 |
| 1 | 9 | 1 | 2 | 22 | 99 | 111 | 105 |
| 1 | 7 | 2 | 36 | 31 | 89 | 104 | 96 |
| 1 | 12 | 1 | 24 | 34 | 57 | 51 | 50 |
| 1 | 6 | 2 | 38 | 37 | 99 | 100 | 99 |
| 1 | 9 | 2 | 14 | 25 | 58 | 113 | 85 |
| 1 | 14 | 2 | 18 | 20 | 97 | 82 | 88 |
| 1 | 15 | 1 | 24 | 16 | 94 | 146 | 120 |
| 1 | 14 | 1 | 20 | 21 | 82 | 107 | 93 |
| 1 | 9 | 2 | 33 | 34 | 92 | 83 | 87 |
| 1 | 7 | 2 | 36 | 27 | 89 | 108 | 98 |
| 1 | 12 | 2 | 18 | 22 | 69 | 93 | 78 |
| 1 | 8 | 1 | 31 | 26 | 87 | 114 | 100 |
| 1 | 7 | 1 | 33 | 30 | 97 | 113 | 105 |
| 1 | 15 | 2 | 27 | 33 | 82 | 94 | 87 |
| 1 | 6 | 2 | 28 | 26 | 85 | 106 | 94 |
| 1 | 14 | 2 | 24 | 23 | 89 | 92 | 89 |
| 1 | 7 | 1 | 30 | 23 | 85 | 79 | 80 |
| 1 | 13 | 1 | 24 | 23 | 92 | 129 | 111 |
| 1 | 12 | 1 | 29 | 24 | 95 | 114 | 104 |
| 1 | 6 | 1 | 38 | 31 | 76 | 99 | 85 |
| 1 | 7 | 1 | 31 | 39 | 80 | 110 | 94 |
| 1 | 9 | 1 | 28 | 32 | 66 | 90 | 75 |
| 1 | 12 | 2 | 22 | 23 | 67 | 85 | 73 |
| 1 | 15 | 1 | 22 | 16 | 63 | 94 | 76 |
| 1 | 10 | 1 | 27 | 28 | 87 | 127 | 107 |
| 1 | 9 | 1 | 24 | 33 | 79 | 101 | 88 |
| 1 | 13 | 2 | 36 | 34 | 82 | 99 | 89 |
| 1 | 12 | 2 | 10 | 38 | 82 | 113 | 96 |
| 1 | 6 | 2 | 30 | 21 | 70 | 80 | 72 |
| 1 | 11 | 2 | 27 | 31 | 81 | 115 | 97 |
| 1 | 15 | 2 | 34 | 33 | 72 | 85 | 76 |
| 1 | 4 | 1 | 35 | 34 | 101 | 112 | 107 |
| 1 | 4 | 2 | 27 | 27 | 95 | 112 | 104 |
| 1 | 3 | 1 | 23 | 26 | 81 | 92 | 85 |
| 1 | 4 | 1 | 27 | 20 | 61 | 97 | 76 |
| 1 | 4 | 1 | 2 | 27 | 94 | 97 | 95 |
| 1 | 3 | 1 | 32 | 28 | 85 | 91 | 86 |
| 1 | 4 | 1 | 33 | 31 | 76 | 105 | 89 |
| 1 | 4 | 1 | 32 | 28 | 72 | 84 | 76 |
| 1 | 4 | 2 | 35 | 37 | 97 | 95 | 96 |
| 1 | 5 | 1 | 35 | 34 | 95 | 108 | 101 |
| 1 | 4 | 2 | 30 | 34 | 97 | 118 | 108 |
| 1 | 4 | 2 | 34 | 23 | 87 | 118 | 102 |
| 1 | 5 | 2 | 18 | 25 | 74 | 86 | 77 |
| 1 | 4 | 1 | 38 | 25 | 66 | 89 | 74 |
| 1 | 6 | 2 | 36 | 23 | 86 | 100 | 92 |
| 2 | 14 | 1 | 42 | 38 | 72 | 78 | 72 |
| 2 | 7 | 2 | 40 | 34 | 85 | 97 | 90 |
| 2 | 7 | 1 | 40 | 34 | 80 | 107 | 92 |
| 2 | 13 | 2 | 41 | 33 | 67 | 80 | 71 |
| 2 | 6 | 1 | 41 | 32 | 85 | 90 | 86 |
| 2 | 15 | 1 | 41 | 30 | 79 | 83 | 79 |
| 2 | 12 | 1 | 43 | 32 | 70 | 101 | 83 |
| 2 | 9 | 1 | 66 | 25 | 105 | 121 | 114 |
| 2 | 9 | 2 | 51 | 39 | 92 | 108 | 100 |
| 2 | 8 | 1 | 44 | 31 | 89 | 100 | 93 |
| 2 | 14 | 2 | 64 | 38 | 74 | 110 | 91 |
| 2 | 9 | 1 | 43 | 32 | 86 | 111 | 98 |
| 2 | 11 | 2 | 43 | 24 | 87 | 97 | 91 |
| 2 | 7 | 1 | 40 | 37 | 51 | 51 | 46 |
| 2 | 9 | 2 | 40 | 35 | 80 | 94 | 85 |
| 2 | 4 | 1 | 47 | 22 | 87 | 80 | 82 |
| 2 | 3 | 2 | 44 | 34 | 94 | 101 | 97 |
| 2 | 5 | 2 | 45 | 29 | 91 | 92 | 91 |
| 2 | 4 | 1 | 41 | 34 | 92 | 100 | 92 |
| 2 | 5 | 2 | 51 | 30 | 81 | 77 | 77 |
| 2 | 3 | 1 | 42 | 32 | 111 | 108 | 111 |
| 2 | 3 | 1 | 50 | 36 | 75 | 85 | 78 |
| 3 | 10 | 1 | 68 | 53 | 75 | 93 | 82 |
| 3 | 10 | 2 | 53 | 49 | 87 | 100 | 93 |
| 3 | 9 | 1 | 48 | 40 | 76 | 97 | 85 |
| 3 | 6 | 1 | 41 | 40 | 76 | 79 | 75 |
| 3 | 5 | 1 | 45 | 47 | 76 | 97 | 85 |
| 3 | 12 | 2 | 62 | 45 | 92 | 71 | 80 |
| 3 | 6 | 1 | 49 | 43 | 91 | 111 | 101 |
| 3 | 7 | 2 | 52 | 58 | 82 | 99 | 89 |
| 3 | 12 | 2 | 61 | 48 | 80 | 85 | 80 |
| 3 | 8 | 1 | 41 | 50 | 91 | 99 | 94 |
| 3 | 6 | 1 | 59 | 40 | 81 | 97 | 88 |
| 3 | 6 | 1 | 57 | 58 | 97 | 111 | 104 |
| 3 | 8 | 1 | 58 | 57 | 76 | 104 | 88 |
| 3 | 11 | 2 | 40 | 51 | 85 | 93 | 88 |
| 3 | 9 | 1 | 57 | 48 | 80 | 90 | 83 |
| 3 | 8 | 1 | 48 | 43 | 100 | 107 | 104 |
| 3 | 4 | 1 | 57 | 43 | 86 | 108 | 96 |
| 3 | 4 | 1 | 51 | 49 | 79 | 78 | 76 |
| 3 | 4 | 1 | 59 | 47 | 70 | 95 | 80 |
| 3 | 3 | 1 | 44 | 45 | 84 | 78 | 79 |
| 3 | 3 | 2 | 42 | 45 | 69 | 86 | 75 |
Body Temp
| 98.6 |
| 98.6 |
| 98.0 |
| 98.0 |
| 99.0 |
| 98.4 |
| 98.4 |
| 98.4 |
| 98.4 |
| 98.6 |
| 98.6 |
| 98.8 |
| 98.6 |
| 97.0 |
| 97.0 |
| 98.8 |
| 97.6 |
| 97.7 |
| 98.8 |
| 98.0 |
| 98.0 |
| 98.3 |
| 98.5 |
| 97.3 |
| 98.7 |
| 97.4 |
| 98.9 |
| 98.6 |
| 99.5 |
| 97.5 |
| 97.3 |
| 97.6 |
| 98.2 |
| 99.6 |
| 98.7 |
| 99.4 |
| 98.2 |
| 98.0 |
| 98.6 |
| 98.6 |
| 97.2 |
| 98.4 |
| 98.6 |
| 98.2 |
| 98.0 |
| 97.8 |
| 98.0 |
| 98.4 |
| 98.6 |
| 98.6 |
| 97.8 |
| 99.0 |
| 96.5 |
| 97.6 |
| 98.0 |
| 96.9 |
| 97.6 |
| 97.1 |
| 97.9 |
| 98.4 |
| 97.3 |
| 98.0 |
| 97.5 |
| 97.6 |
| 98.2 |
| 98.5 |
| 98.8 |
| 98.7 |
| 97.8 |
| 98.0 |
| 97.1 |
| 97.4 |
| 99.4 |
| 98.4 |
| 98.6 |
| 98.4 |
| 98.5 |
| 98.6 |
| 98.3 |
| 98.7 |
| 98.8 |
| 99.1 |
| 98.6 |
| 97.9 |
| 98.8 |
| 98.0 |
| 98.7 |
| 98.5 |
| 98.9 |
| 98.4 |
| 98.6 |
| 97.1 |
| 97.9 |
| 98.8 |
| 98.7 |
| 97.6 |
| 98.2 |
| 99.2 |
| 97.8 |
| 98.0 |
| 98.4 |
| 97.8 |
| 98.4 |
| 97.4 |
| 98.0 |
| 97.0 |
Hypothesis Testing Steps
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


