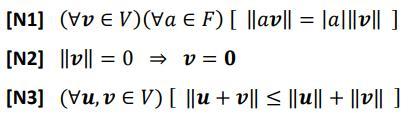
Definition: Given a Vector Space V over Field F (R or C), a norm is a mapping II-|l : V R which satisfies the following properties: [N1] (VV E V)Va E F) [ ||av|| = la|||v|| ] [N2] ||v|| = 0 = v = 0 [N3] (Vu,vEV) [ u + < 1lul + ||1 ] QUESTION 1 Consider Vector Space V over Field F (IRor C) with a norm ||| Prove (from the Definition of norm) that v = 0 = ||v|| = 0 QUESTION 2 Consider Vector Space V over Field F (R or C) with a norm ||:|| Prove (from the Definition of norm) that (Vv E V) [ ||v|| > 0 ]