QUESTION 1:

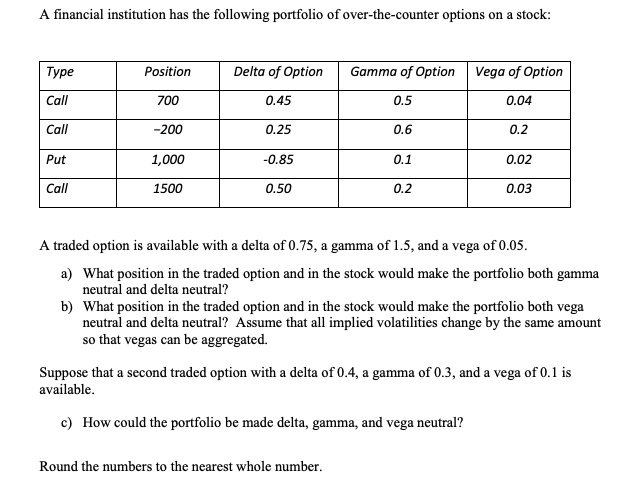
QUESTION 2:

QUESTION 3:

A financial institution has the following portfolio of over-the-counter options on a stock: Type Position Delta of Option Gamma of Option Vega of Option Call 700 0.45 0.5 0.04 Call -200 0.25 0.6 0.2 Put 1,000 -0.85 0.1 0.02 Call 1500 0.50 0.2 0.03 A traded option is available with a delta of 0.75, a gamma of 1.5, and a vega of 0.05. a) What position in the traded option and in the stock would make the portfolio both gamma neutral and delta neutral? b) What position in the traded option and in the stock would make the portfolio both vega neutral and delta neutral? Assume that all implied volatilities change by the same amount so that vegas can be aggregated. Suppose that a second traded option with a delta of 0.4, a gamma of 0.3, and a vega of 0.1 is available. c) How could the portfolio be made delta, gamma, and vega neutral? Round the numbers to the nearest whole number. A company is currently awaiting the outcome of a major lawsuit. This is expected to be known within one month. The stock price is currently $100. If the outcome is positive, the stock price is expected to be $120 at the end of one month. If the outcome is negative, it is expected to be $90 at this time. The one-month risk-free interest rate is 5% per annum. a) What is the risk-neutral probability of a positive outcome in a one-step binomial model? b) Use a one-step binomial model to find the values of one-month call options with strike prices of $95, $100, $105, $110, and $115? c) Use DerivaGem to calculate a volatility smile for one-month call options. d) Verify that the same volatility smile is obtained for one-month put options with the same strike prices as in part b. Suppose that Australian dollar (AUD) is currently worth $0.7, the risk-free rate in Australia and United States are 5% and 1% per annum, respectively, and the volatility of AUD/USD is 10% per annum. a) Use Black-Scholes-Merton formulas to calculate the value of a 3-month European call option to buy one AUD for 0.75 USD. b) What is the price of a 3-month European put option to sell 0.75 USD for one AUD? c) What is the price of a put option to sell 0.75 USD for one AUD in nine month? Now suppose that a company will receive 1 million AUD in three months. The company decides to use a range forward contract with the higher strike equal to $0.75. d) What should the lower strike be to create a zero-cost contract? Use DerivaGem. e) What positions in calls and puts should the company take? f) Show that your answer to (d) does not depend on interest rates providing the interest rate differential between the two currencies, r- rf, remains the same. Outline solutions and indicate intermediate steps and calculations. A financial institution has the following portfolio of over-the-counter options on a stock: Type Position Delta of Option Gamma of Option Vega of Option Call 700 0.45 0.5 0.04 Call -200 0.25 0.6 0.2 Put 1,000 -0.85 0.1 0.02 Call 1500 0.50 0.2 0.03 A traded option is available with a delta of 0.75, a gamma of 1.5, and a vega of 0.05. a) What position in the traded option and in the stock would make the portfolio both gamma neutral and delta neutral? b) What position in the traded option and in the stock would make the portfolio both vega neutral and delta neutral? Assume that all implied volatilities change by the same amount so that vegas can be aggregated. Suppose that a second traded option with a delta of 0.4, a gamma of 0.3, and a vega of 0.1 is available. c) How could the portfolio be made delta, gamma, and vega neutral? Round the numbers to the nearest whole number. A company is currently awaiting the outcome of a major lawsuit. This is expected to be known within one month. The stock price is currently $100. If the outcome is positive, the stock price is expected to be $120 at the end of one month. If the outcome is negative, it is expected to be $90 at this time. The one-month risk-free interest rate is 5% per annum. a) What is the risk-neutral probability of a positive outcome in a one-step binomial model? b) Use a one-step binomial model to find the values of one-month call options with strike prices of $95, $100, $105, $110, and $115? c) Use DerivaGem to calculate a volatility smile for one-month call options. d) Verify that the same volatility smile is obtained for one-month put options with the same strike prices as in part b. Suppose that Australian dollar (AUD) is currently worth $0.7, the risk-free rate in Australia and United States are 5% and 1% per annum, respectively, and the volatility of AUD/USD is 10% per annum. a) Use Black-Scholes-Merton formulas to calculate the value of a 3-month European call option to buy one AUD for 0.75 USD. b) What is the price of a 3-month European put option to sell 0.75 USD for one AUD? c) What is the price of a put option to sell 0.75 USD for one AUD in nine month? Now suppose that a company will receive 1 million AUD in three months. The company decides to use a range forward contract with the higher strike equal to $0.75. d) What should the lower strike be to create a zero-cost contract? Use DerivaGem. e) What positions in calls and puts should the company take? f) Show that your answer to (d) does not depend on interest rates providing the interest rate differential between the two currencies, r- rf, remains the same. Outline solutions and indicate intermediate steps and calculations