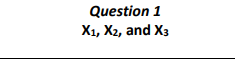
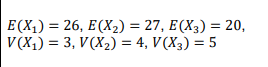
Question 1 X1, X2, and X3 E(X) = 26, E(X) = 27, E(X) = 20, V(X1) = 3, V(X2) = 4, V(X3) = 5 = = Question 1: Functions of Random Variables and Sampling distributions (55 points] Assume that X, X2, and X, are independent and normally distributed random variables with expected values E(X1), E(X2), E(X3), variances V(X1), V(X2), V(X3), and Y = -4+ 9x2 3x2 + 4X3, is a linear function of these random variables. Use your personally assigned expected values and variances for X1, X2, and X; to answer the following questions. The values are based on the last digit of your student ID. (a) E(Y) [5 points) (b) V(Y) [10 points) (c) P(Y > 203) [10 points) (d) P(205.3 SY 239.9). [10 points)