Question 1
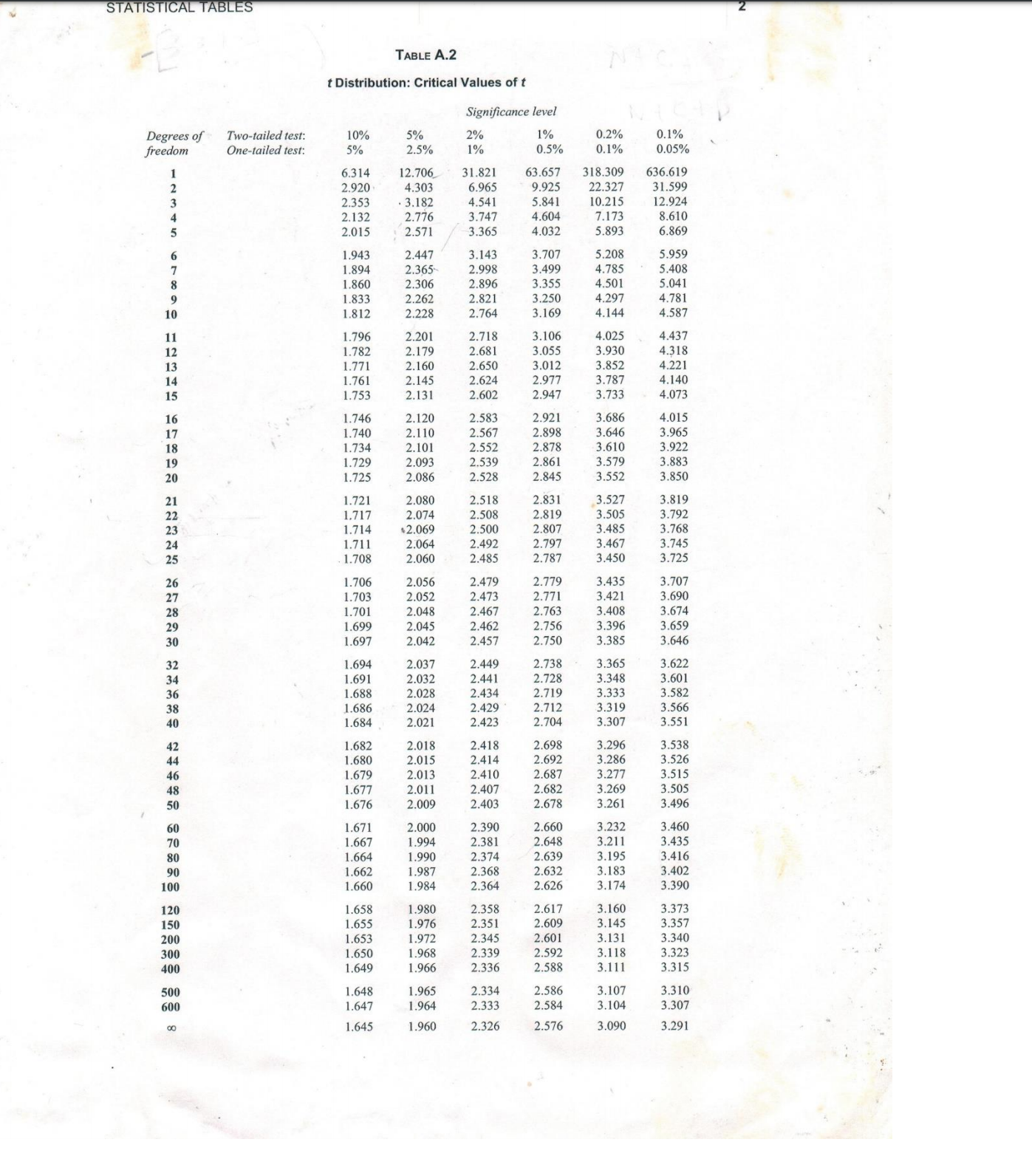
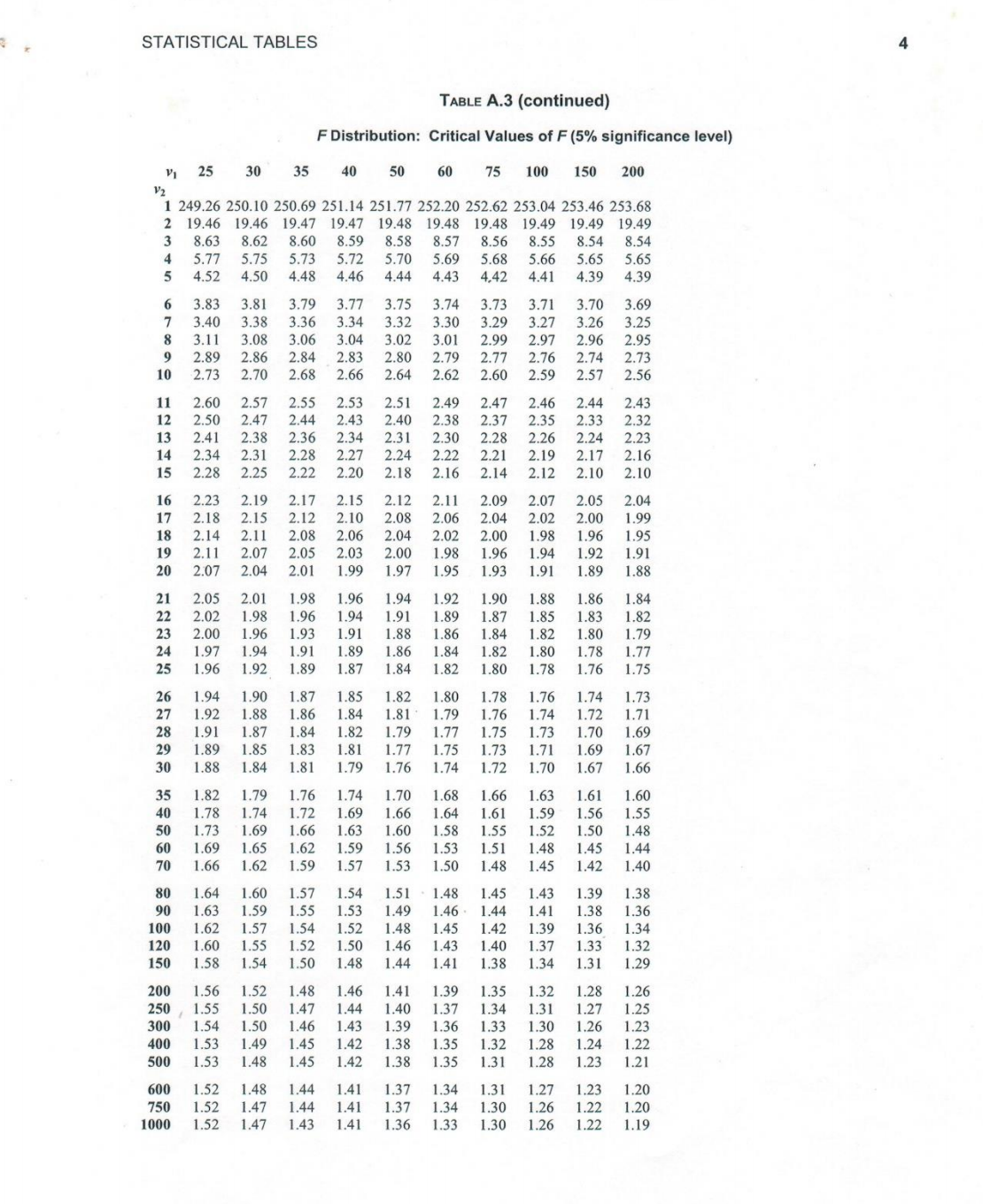
You are an econometrician working in the Ministry of Finance in Trinidad and Tobago and using a database consisting of 108 monthly observations on automobile accidents for Trinidad and Tobago between January 201 1 and December 2019, you estimate the following model: log( totacct) = Bo + Bit + Bzfeb. + B3mart ... + Bizdect + Ht where totacc is the total number of accidents, t is time (measured in months), and feb,, mart, dec, are dummy variables indicating whether time period t corresponds to the appropriate month. You obtain the following OLS results: Source SS df MS Number of obs = 108 Model 1 . 00244071 . 083536726 F ( 12, 95) = 31 . 06 Residual . 255496765 12 Prob > F 95 0 . 0000 00268944 R-squared 0. 7969 Total I 1 . 25793748 Adj R-squared . 011756425 0 . 7712 107 Root MSE . 05186 1totacc Coef . Std. Err. P>Itl [95% Conf. Interval] t 0027471 0001611 0 . 000 feb - . 0426865 . 0244475 17.06 -1 . 75 0 . 084 . 0024274 - . 0912208 0030669 mar . 0798245 0244491 3.26 0 . 002 apr . 0244517 0 . 76 0 . 452 . 031287 . 0058479 . 0184849 - . 030058 1283621 may 0320981 . 0244554 0670277 jun . 0201918 . 0244602 1 . 31 0 . 83 0. 193 0 . 411 - . 0164521 jul 0375826 . 024466 1 . 54 - . 0283678 0806483 0 . 128 . 0687515 aug . 053983 . 0244729 2.21 - . 0109886 . 0861538 sep . 042361 . 0244809 0821135 1 . 73 0. 030 0. 087 0053981 - . 0062397 . 1025679 oct . 0244899 3.35 0 . 001 . 0909617 0712785 . 0334949 2. 91 dec . 0961572 . 0244999 . 130732 . 0245111 3.92 0 . 005 0 . 000 . 02264 1199171 cons 10 . 46857 . 0474966 . 0190028 550.89 1448178 0 . 000 10 . 43084 10 . 50629 The team meeting will be held in 3 days from the date of the assignment and because of the limitation of time the Chief economist has given you the following guidelines: (a) Is there a trend in total accidents? [4 marks] (b) Is there seasonality in total accidents? [3 marks] (c) Consider the following change in the time series model: yt = Q1)t-1 + ut where ut follows a white noise process. What is the condition we need to impose on 41 in order for the series yt to be weakly stationary? Why? [8 marks] (d) Consider the following change in the time series model: yt = Bo + BIXt-1 + B2*t-2 + ut where It is some outcome variable of interest, and Xt-1 and Xt-2 are strictly exogenous Page 9 of 15 explanatory variables. How would you test for the presence of serial correlation in the residual u.?STATISTICAL TABLES TABLE A.2 t Distribution: Critical Values of t Significance level Degrees of Two-tailed test: 10% 1% 0.2% 0.1% One-tailed test: 5% 25% 1% 0.5% 0.1% 0.05% 6.314 2.706 53.657 318.309 636.619 2.920 4.303 6.965 22.327 31.599 2.353 3.182 4.541 5.841 10.215 12.924 2.132 2.776 3.747 4.604 7.173 8.610 2.571 3.365 4.032 5.893 6.869 1.943 2.447 3.143 3.707 5.959 1.894 2.365 2.998 3.499 4.785 5.408 1.860 2.306 2.896 3.355 4.50 5.041 1.833 2.262 2.821 3.250 4.781 2.228 2.764 3.169 4.144 4.587 1.796 2.201 2.718 3.106 4.025 4.437 1.782 2.17 2.681 3.055 3.930 4.318 1.771 2 650 3.012 3.852 4.221 1.761 2.14 2.977 3.787 4.140 1.753 13 2.602 2.947 3.733 4.073 2.12 2.583 2.921 3.686 4.015 1.740 2.110 2.567 2.898 3.646 1.734 2 101 2.552 2.878 3.610 3.922 1.729 .539 2.861 3.579 1.725 2.528 2 845 3.552 3.850 1.721 2.83 3.527 3.819 2.074 2.508 2.819 3.505 3.792 1.714 2.500 2.807 1.711 2.064 2.797 3.467 3.745 1.708 2.060 2.485 2.787 3.450 3.725 1.706 2.056 2.47 2.779 3.435 3.707 2.473 2.771 3.421 3.690 1.701 2.467 2.763 3.408 3.674 1.699 2.045 2.46 2.756 3.396 3.659 1.697 2.457 2.750 3.385 3.646 1.694 2.037 2.738 3.365 3.622 1.691 .032 2.441 2.728 3.348 3.601 1.688 2.434 2.719 3.333 1.686 3.319 3.566 1.684 2.021 2.423 2.704 3.307 3.551 41 2.698 .296 3.538 1.680 2.015 2.414 2.692 3.286 3.526 .679 2.013 2 687 3.277 3.515 .677 2011 2.40 2.682 3.269 3.505 1.676 2.009 2.403 2.678 3.261 3.496 60 1.671 2.39 2.66 3.232 3.460 .667 1.994 2.38 2.648 3.211 3.435 80 .664 1.990 2.639 3.195 3.416 90 .662 2.36 2.632 3.183 100 1.984 2.36 2.626 3.174 3.390 120 1.658 .35 2.61 .16 3.373 1.976 2.351 2.609 3.145 3.357 200 .653 2.601 3.131 3.340 300 .650 1.968 2.33 2.592 3.118 1.649 1.966 3.111 3.315 500 1.648 2.334 2.586 3.107 3.310 1.647 964 2.333 2.584 3.104 3.307 1.645 1.960 2.326 2.576 3.090 3.291\f\f\f