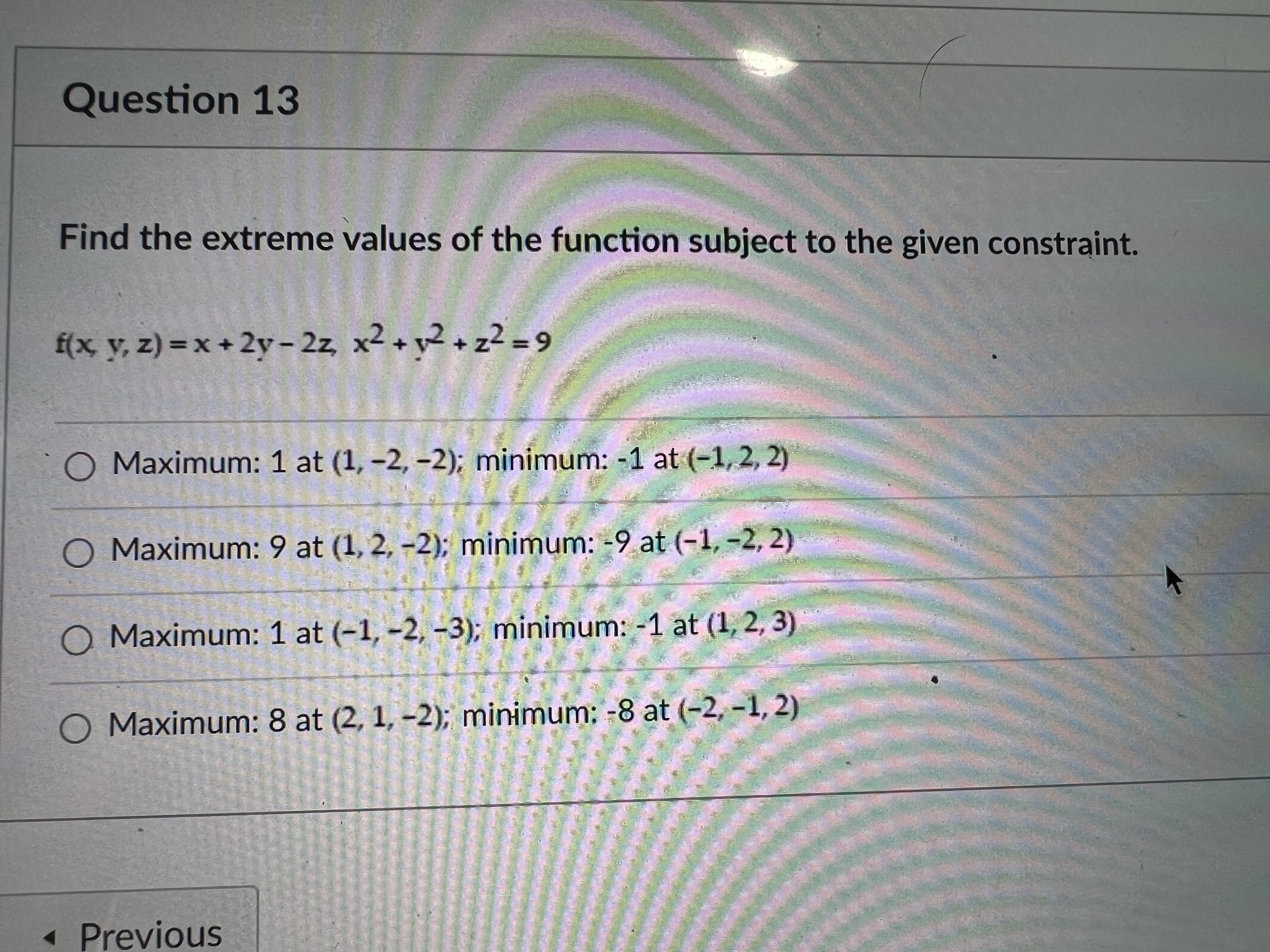
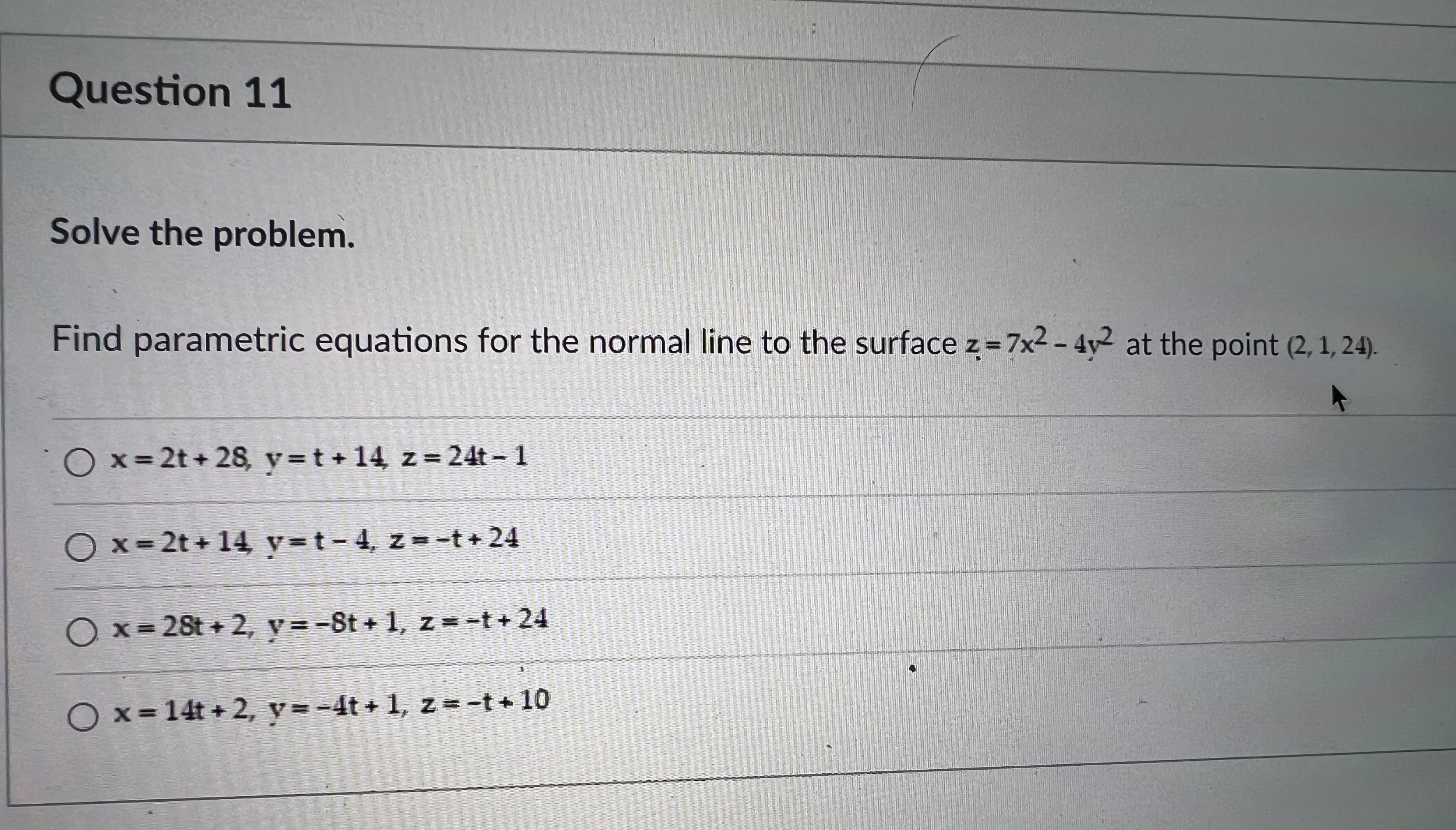
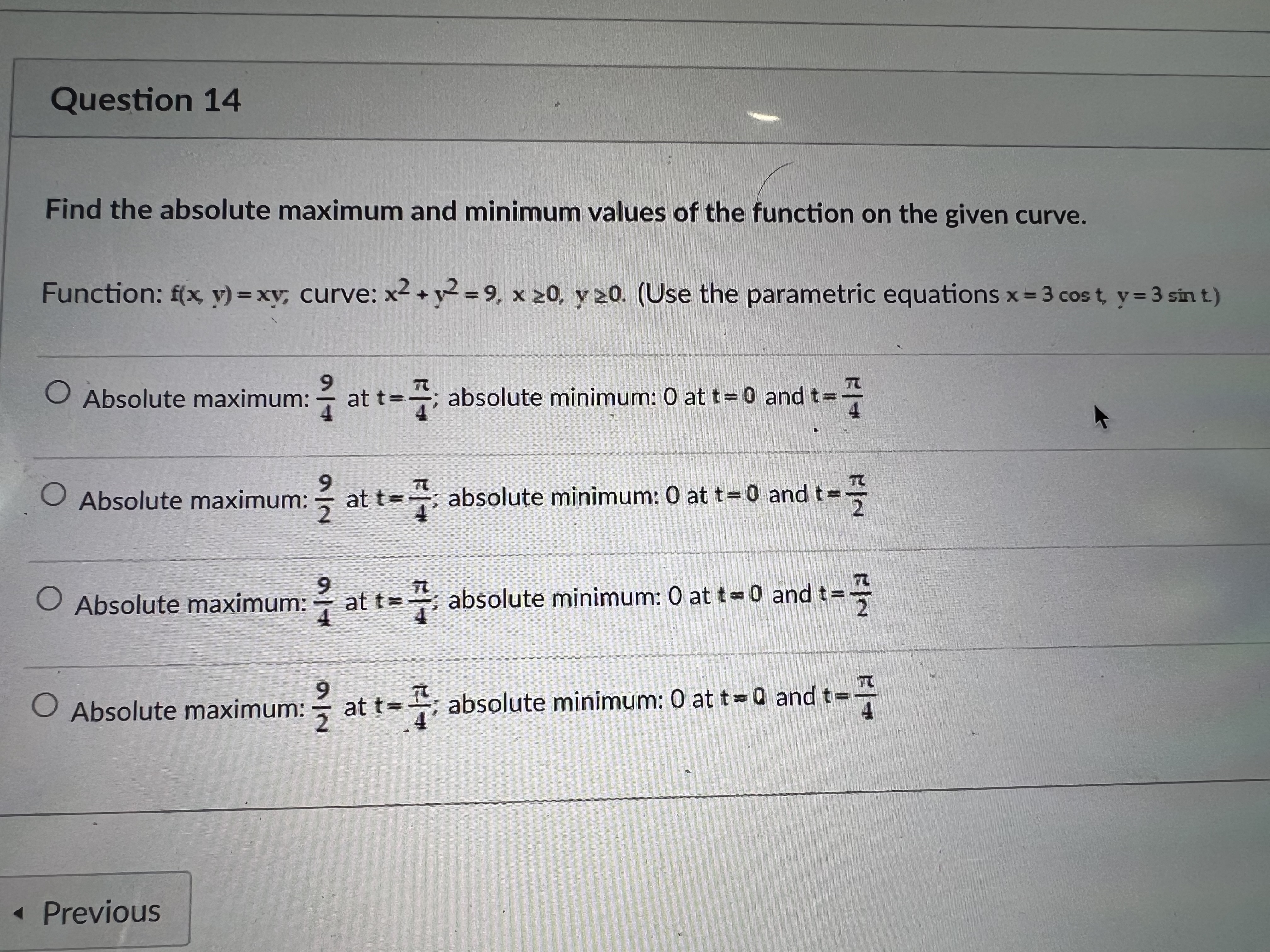
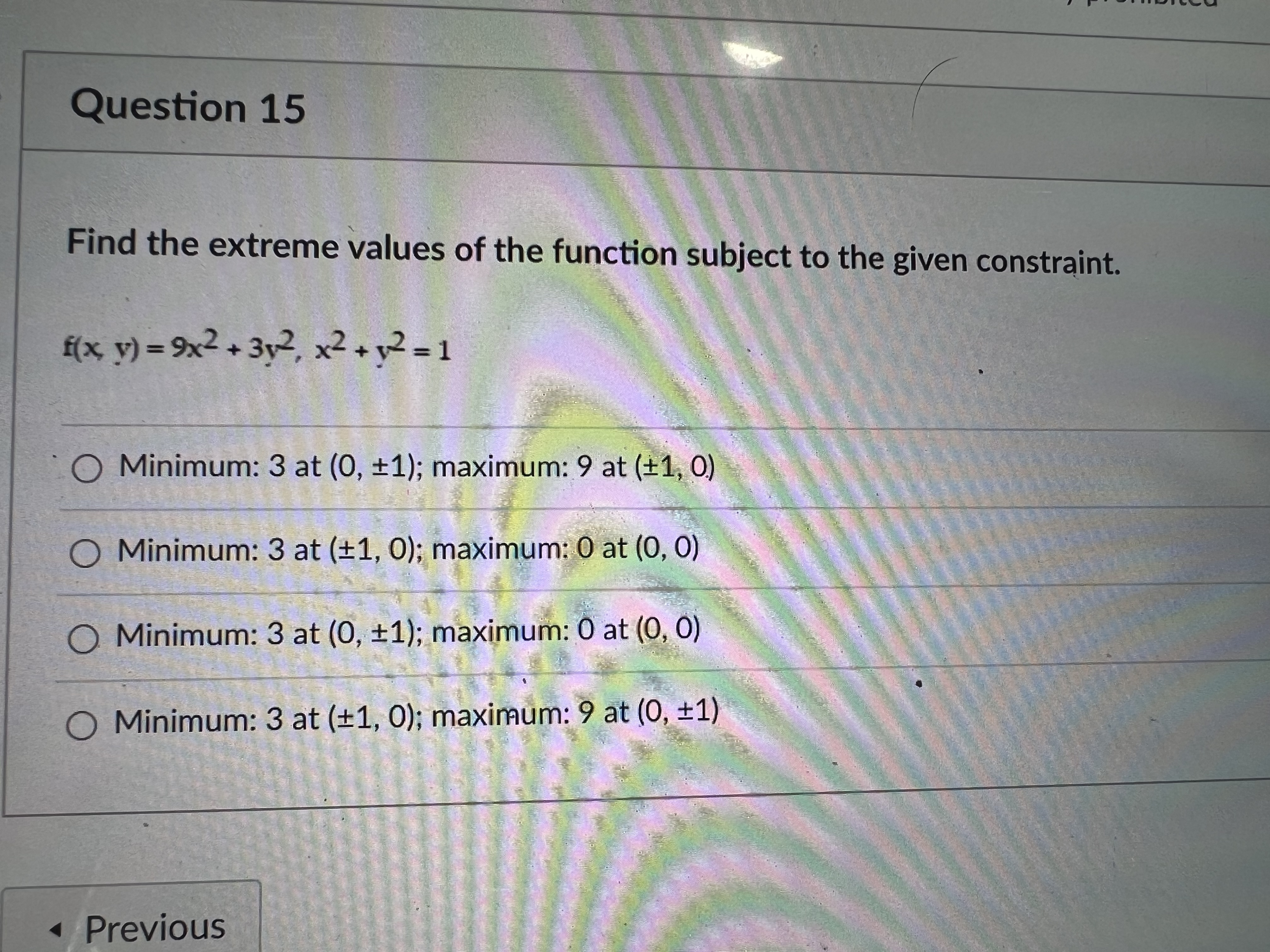
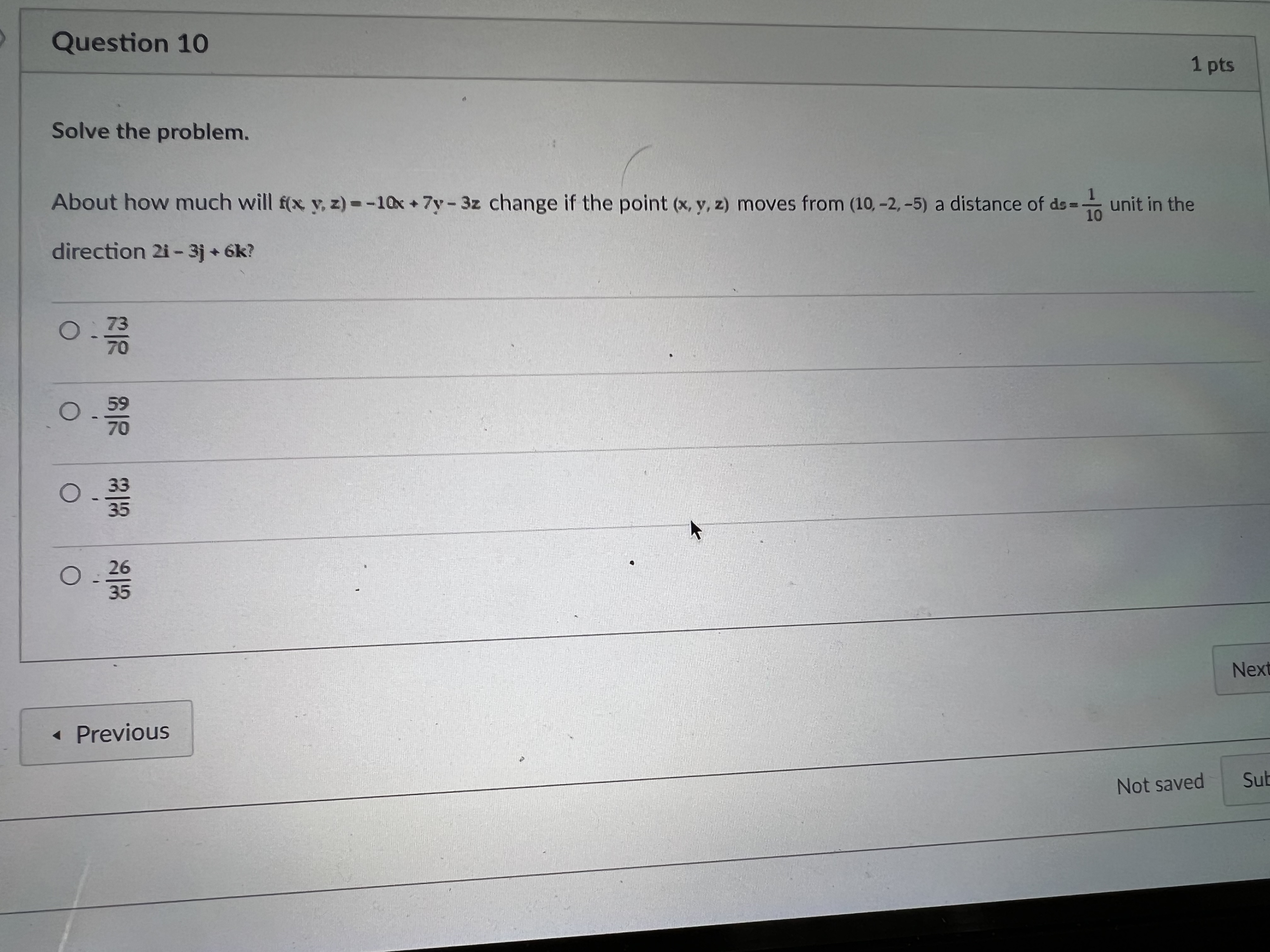
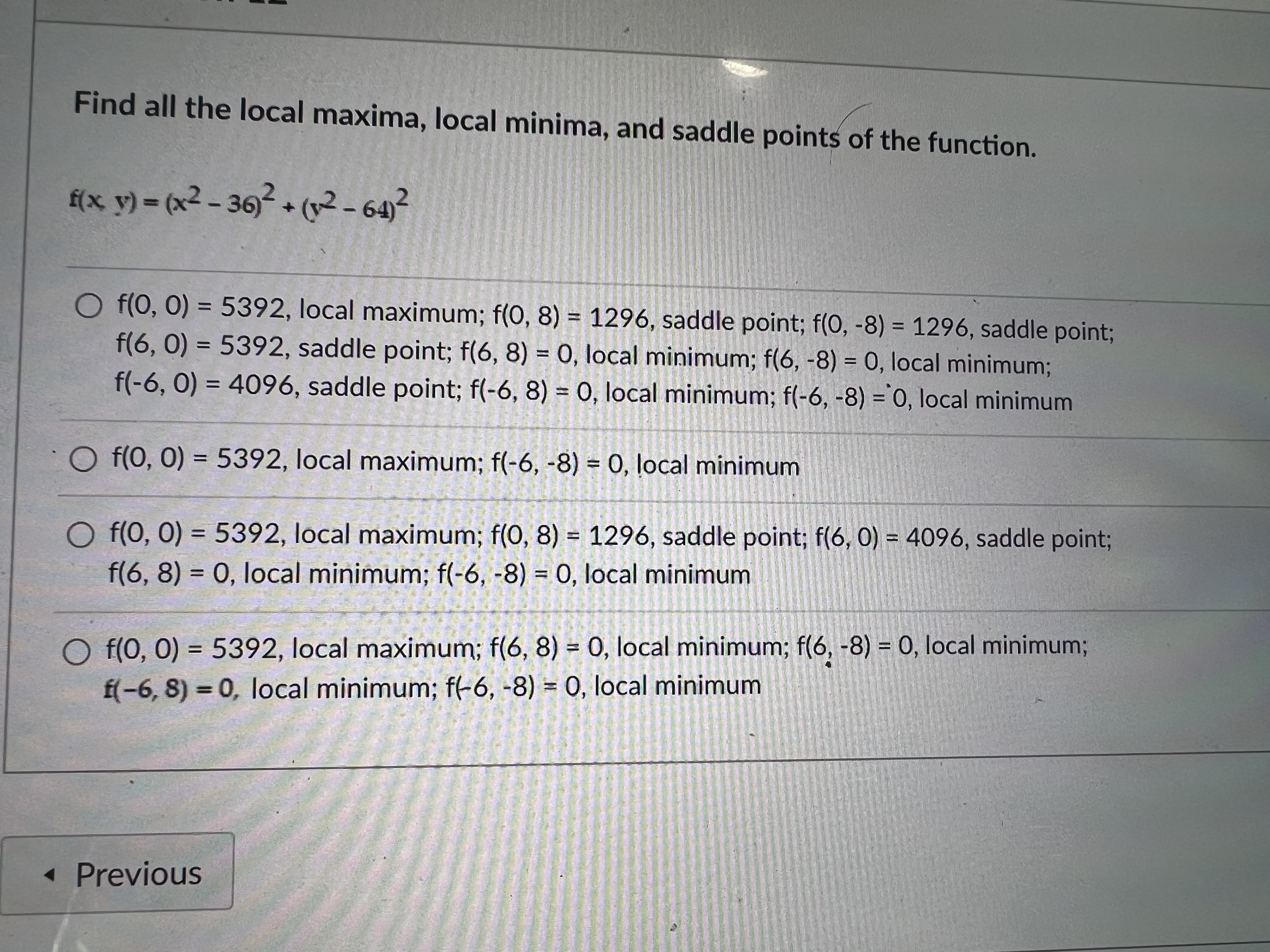
Question 13 Find the extreme values of the function subject to the given constraint. f(x, y, z) = x+2y-2z, x+2+z2=9 Maximum: 1 at (1, -2, -2); minimum: -1 at (-1,2,2) O Maximum: 9 at (1, 2, -2); minimum: -9 at (-1, -2, 2) O Maximum: 1 at (-1, -2, -3); minimum: -1 at (1, 2, 3) O Maximum: 8 at (2, 1, -2); minimum: -8 at (-2, -1, 2) Previous Question 11 Solve the problem. Find parametric equations for the normal line to the surface z=7x - 42 at the point (2, 1, 24). Ox=2t+28, y=t+14, z=24t-1 Ox=2t+14 y=t-4, z=t+24 Ox=28t+2, y=8t+1, z=t+24 Ox=14t+2, y=4t+1, z=-t+10 Question 14 Find the absolute maximum and minimum values of the function on the given curve. Function: f(x, y) = xy, curve: x+12=9, x 20, y 20. (Use the parametric equations x = 3 cost, y = 3 sint) 9 O Absolute maximum: at t=7; absolute minimum: 0 at t=0 and t=1 9 2/2 Absolute maximum: at t=4; absolute minimum: 0 at t=0 and t= O 9 t=1 Absolute maximum: at t=7; absolute minimum: 0 at t=0 and t= 2 9 O Absolute maximum: at t = 1; absolute minimum: 0 at t=0 and t- 2 Previous Question 15 Find the extreme values of the function subject to the given constraint. f(x, y) = 9x + 3y, x + y = 1 O Minimum: 3 at (0, 1); maximum: 9 at (1, 0) O Minimum: 3 at (1, 0); maximum: 0 at (0, 0) O Minimum: 3 at (0, 1); maximum: 0 at (0, 0) Minimum: 3 at (1, 0); maximum: 9 at (0, 1) Previous Question 10 Solve the problem. About how much will f(x, y, z)=-10x+7y-3z change if the point (x, y, z) moves from (10,-2,-5) a distance of ds = 10 unit in the direction 2i - 3j+6k? O 73 70 0.599 70 0.339 O 35 26 35 225 Previous Not saved 1 pts Next Sub Find all the local maxima, local minima, and saddle points of the function. f(x y) = (x-36)+(12-64) Of(0, 0) = 5392, local maximum; f(0, 8) = 1296, saddle point; f(0, -8) = 1296, saddle point; f(6, 0) = 5392, saddle point; f(6, 8) = 0, local minimum; f(6, -8) = 0, local minimum; f(-6, 0) = 4096, saddle point; f(-6, 8) = 0, local minimum; f(-6, -8) = 0, local minimum Of(0, 0) = 5392, local maximum; f(-6, -8) = 0, local minimum Of(0, 0) = 5392, local maximum; f(0, 8) = 1296, saddle point; f(6, 0) = 4096, saddle point; f(6, 8) = 0, local minimum; f(-6, -8) = 0, local minimum Of(0, 0) = 5392, local maximum; f(6, 8) = 0, local minimum; f(6, -8) = 0, local minimum; f(-6, 8) = 0, local minimum; f(-6, -8) = 0, local minimum Previous