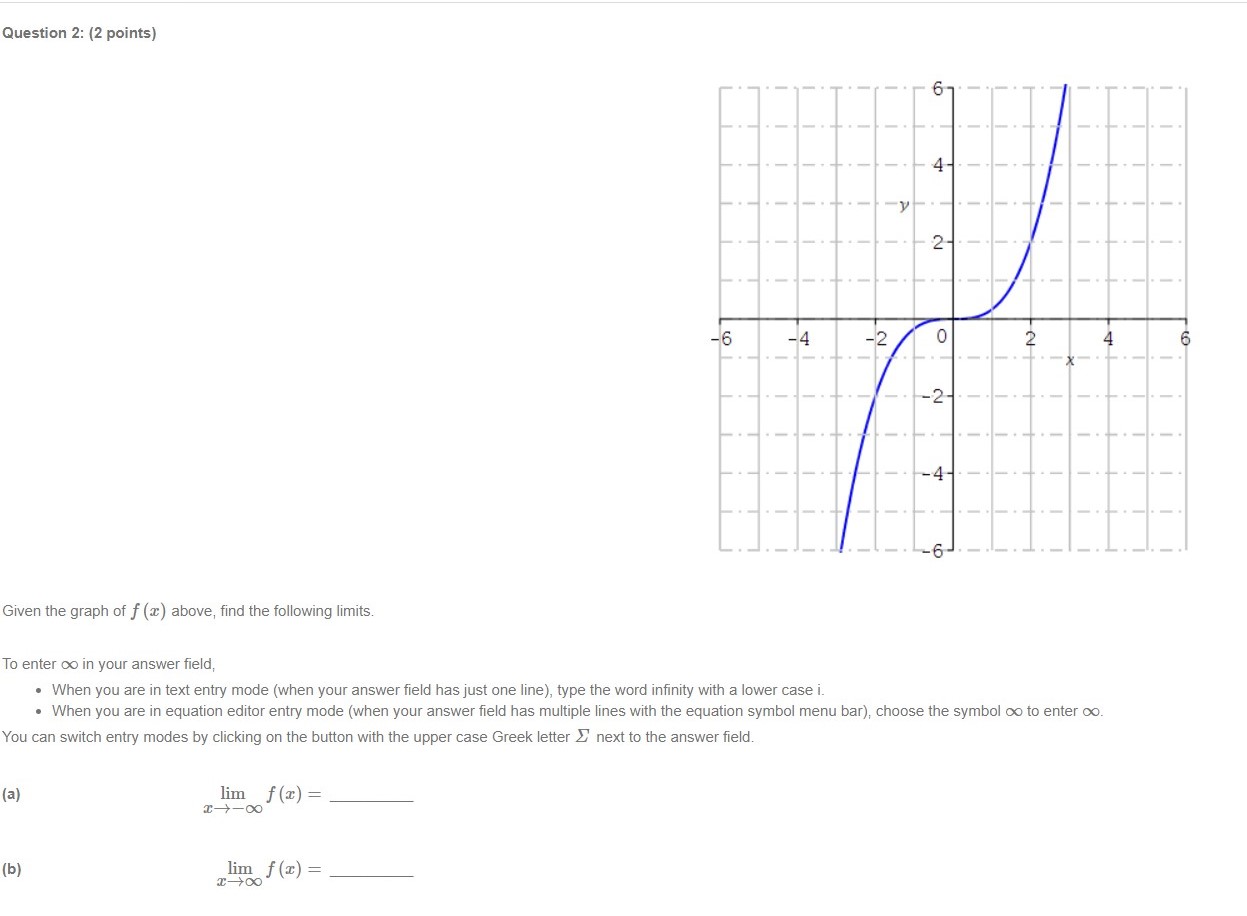
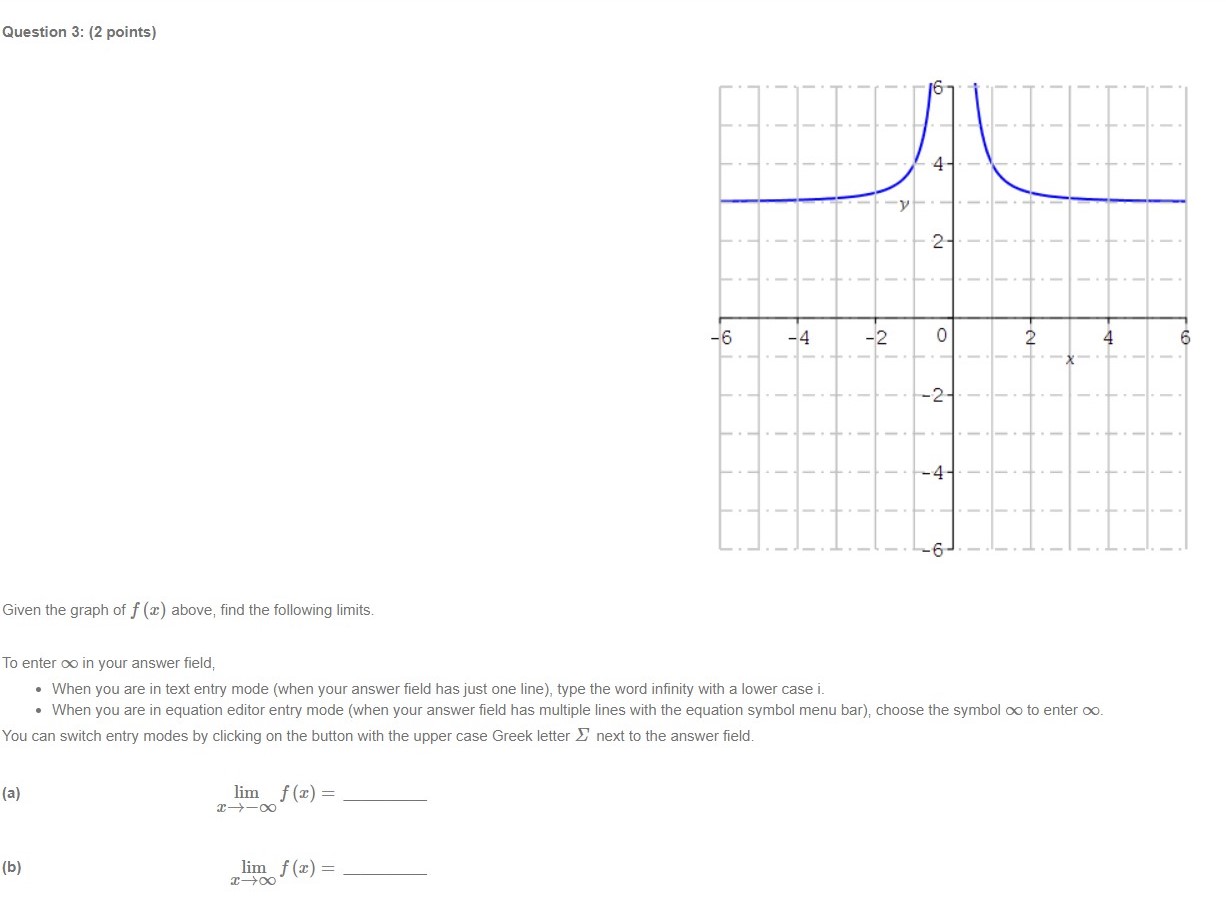
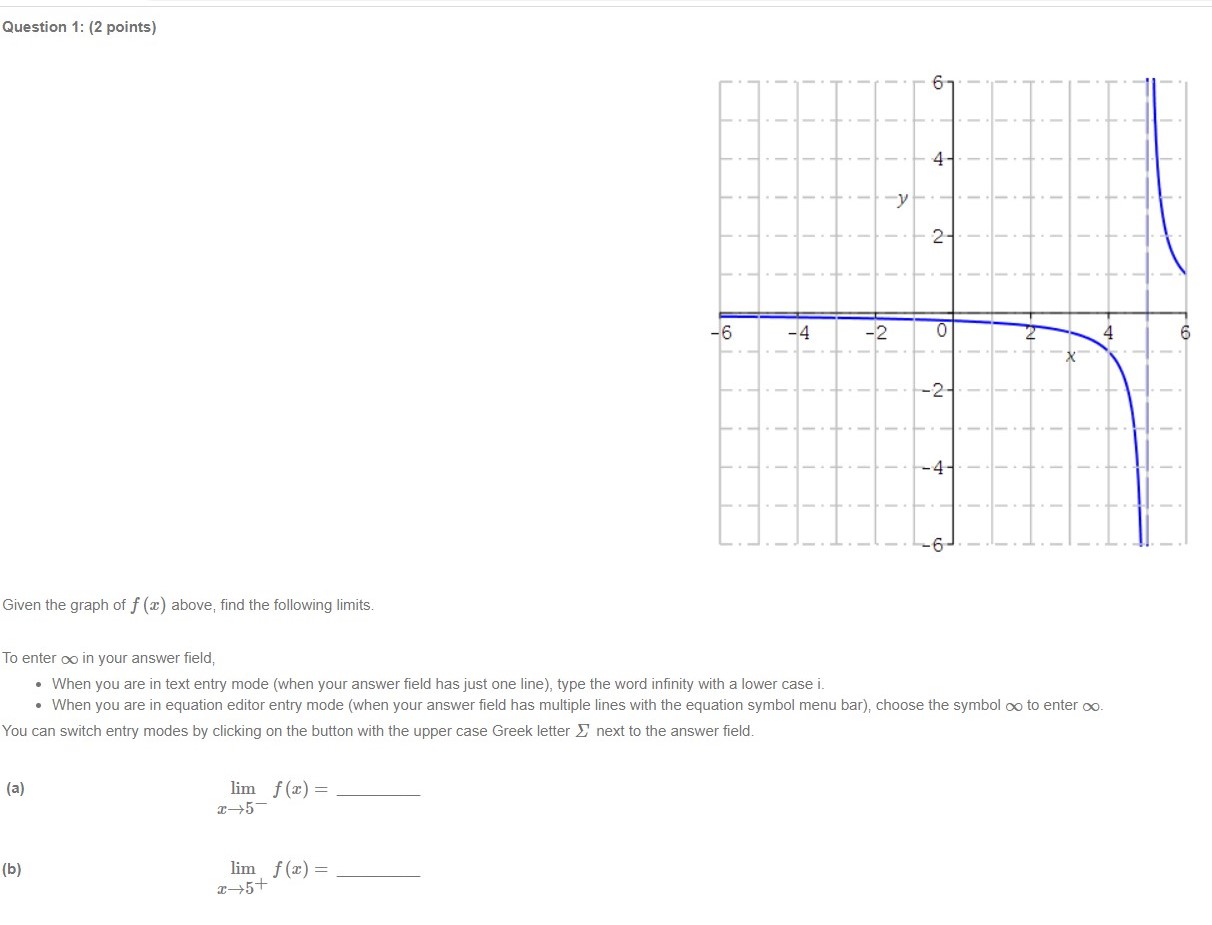
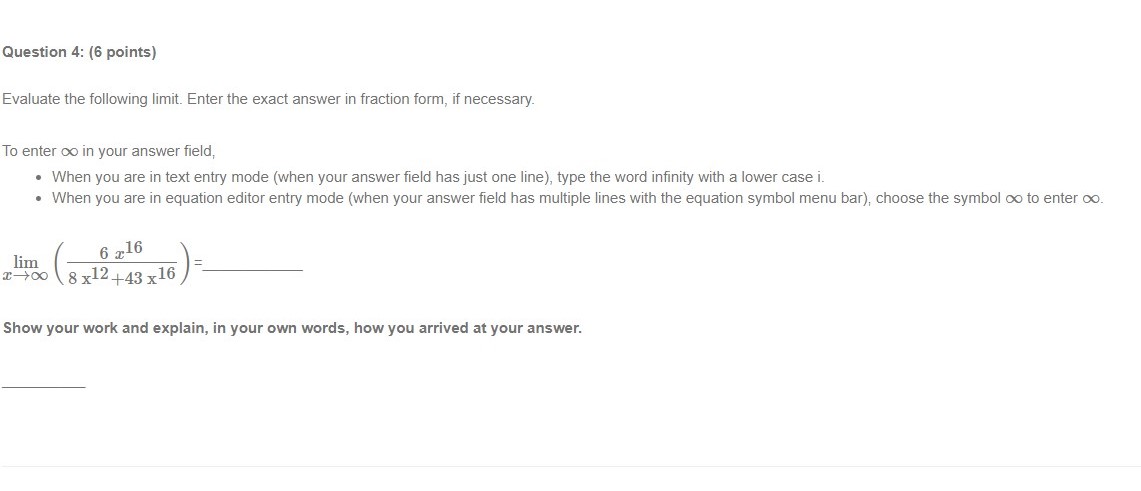
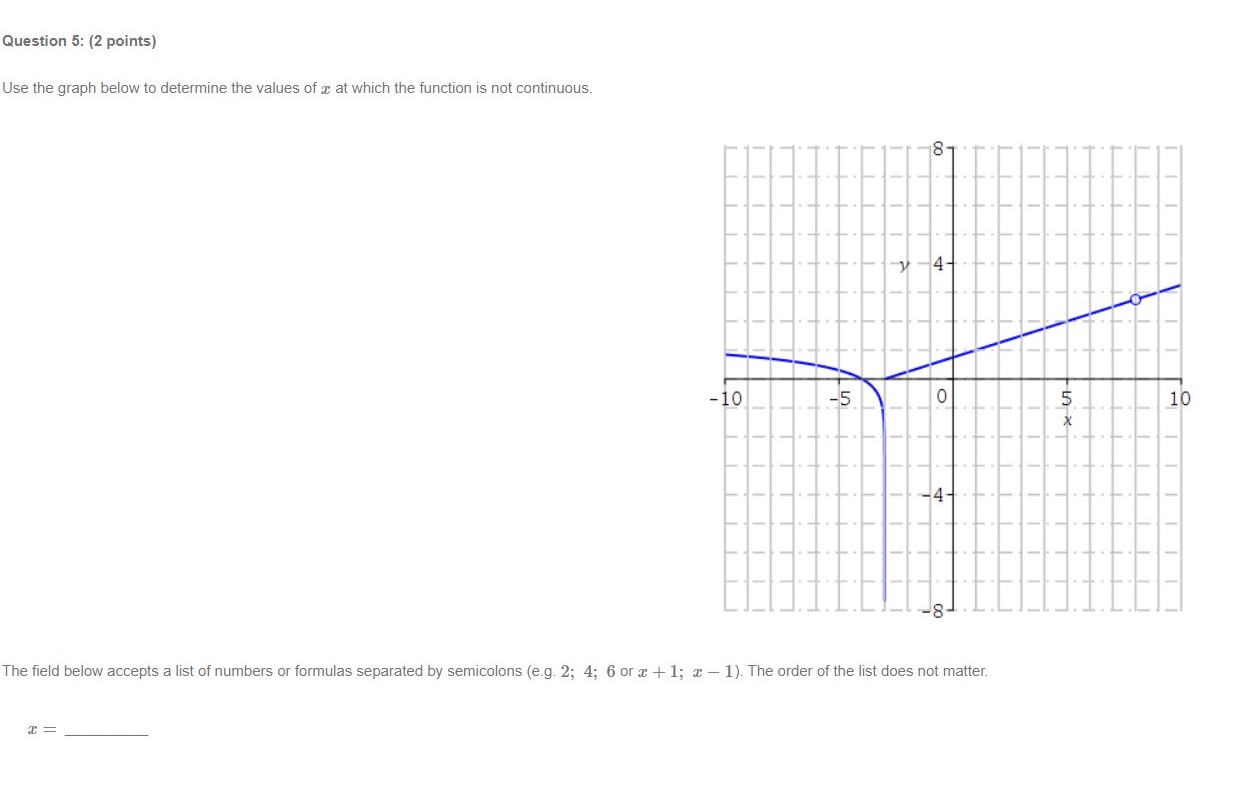
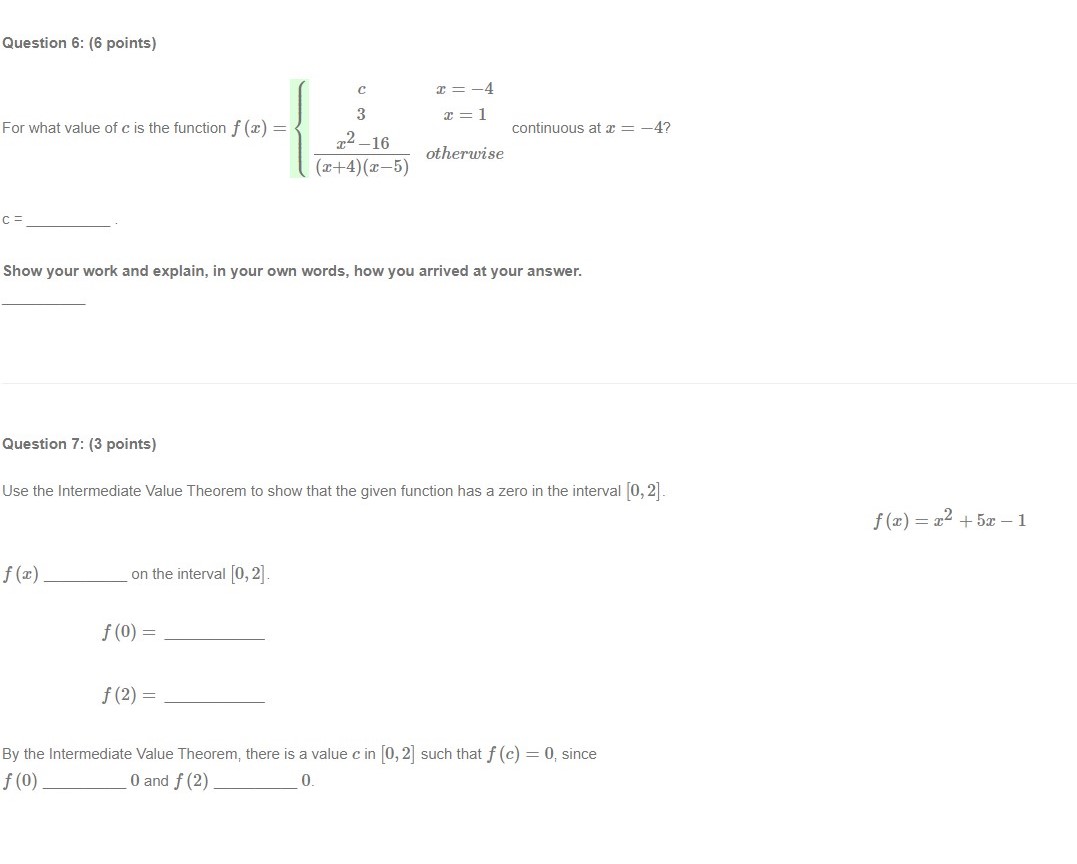
Question 2: (2 points) 4 6 -4 -2 0 -2- -4 Given the graph of f (a) above, find the following limits. To enter co in your answer field, . When you are in text entry mode (when your answer field has just one line), type the word infinity with a lower case i. . When you are in equation editor entry mode (when your answer field has multiple lines with the equation symbol menu bar), choose the symbol co to enter co. You can switch entry modes by clicking on the button with the upper case Greek letter _ next to the answer field. (a) lim f () = (b) lim f (x) =Question 3: (2 points) 2- -6 -4 -2 0 -2- Given the graph of f () above, find the following limits. To enter co in your answer field, . When you are in text entry mode (when your answer field has just one line), type the word infinity with a lower case i. . When you are in equation editor entry mode (when your answer field has multiple lines with the equation symbol menu bar), choose the symbol co to enter co. You can switch entry modes by clicking on the button with the upper case Greek letter _ next to the answer field. (a) lim f (x) = (b) lim f (x) =Question 1: (2 points) 2- 6 -4 -2 0 -2- Given the graph of f () above, find the following limits. To enter co in your answer field, . When you are in text entry mode (when your answer field has just one line), type the word infinity with a lower case i. . When you are in equation editor entry mode (when your answer field has multiple lines with the equation symbol menu bar), choose the symbol co to enter co. You can switch entry modes by clicking on the button with the upper case Greek letter _ next to the answer field. (a) lim f (x) = (b) lim f (x) =Question 4: (6 points) Evaluate the following limit. Enter the exact answer in fraction form, if necessary. To enter co in your answer field, . When you are in text entry mode (when your answer field has just one line), type the word infinity with a lower case i. . When you are in equation editor entry mode (when your answer field has multiple lines with the equation symbol menu bar), choose the symbol co to enter co. lim 8 x12 +43 x16 Show your work and explain, in your own words, how you arrived at your answer.Question 5: (2 points) Use the graph below to determine the values of a at which the function is not continuous. -10 -5 0 10 4- The field below accepts a list of numbers or formulas separated by semicolons (e.g. 2; 4; 6 or x + 1; x - 1). The order of the list does not matter.Question 6: {6 points} (.2 :I: 4 3 = 1 For what value of c is the function f (2:) = 2 continuous at 2 = 4? :E16 aha-wise (I+4)(I5) Show your work and explain, in your own words, how you arrived at your answer. Question T: {3 points} Use the Intermediate Value Theorem to show that the given function has a zero in the interval [0, 2]. f[z]=a:2+52:1 f {3) on the interval [0, 2]. J' (0) = H2) = By the Intermediate Value Theorem, there is a value c in [01 2] such that f (c) = 0. since f(|l]) O and f(2) 0. Question 8: {5 points] The following is Mobius' explanation for a solution to this question. You can use this and other online references as a guide, but your explanation should be in your own words. The derivative of a function of f at a: is given by .l' . f($+h)f(z) f (1:) 2 11m h hi provided the limit exists. 2 Use the denition of the derivative to nd the derivative of f (:3) = 72: + 52 + 1. Enter the fully simplied expression for f (:I: + h.) .f (:3) Do not factor Make sure there is a space between variables, f(=+hJ-f(3) = 3"(3) = Show your work and explain, in your own words, how you arrived at your answers. Question 9: {2 points] Find the derivative off [2!] : 6211 2:4 + 9. flit): Question 10: (2 points) Find the derivative of f (w) = w4 + 2w. Enclose numerators and denominators in parentheses. For example (a - b) / (1 + n). f' (w) = Question 11: (3 points) Given f (9) = 5, f (9) = 11, g(9) = -1, and g' (9) = 9, find the values of the following. (a) (fg)' (9) = (b) Question 12: (6 points) Find the equation of the tangent line to the graph of the function f (x) = (x2 + 7 ) (x - 3) at the point (0, -21). y = Show your work and explain, in your own words, how you arrived at your