Question
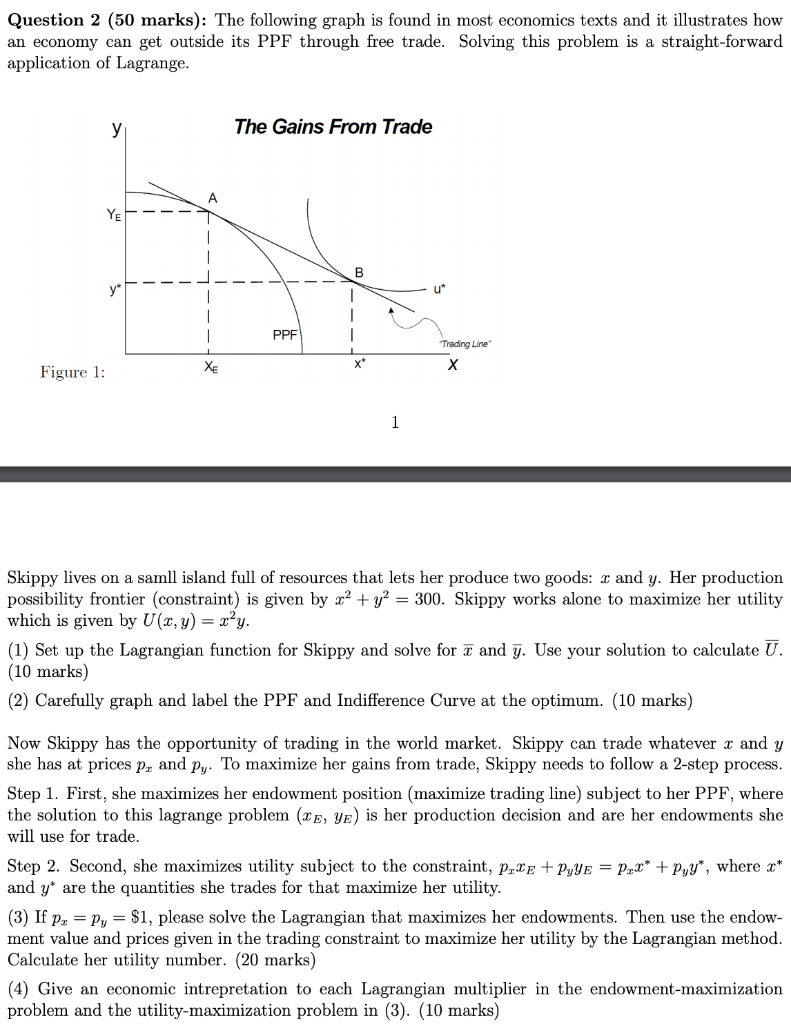
Question 2 (50 marks): The following graph is found in most economics texts and it illustrates how an economy can get outside its PPF through
Question 2 (50 marks): The following graph is found in most economics texts and it illustrates how
an economy can get outside its PPF through free trade. Solving this problem is a straight-forward
application of Lagrange.
1
Skippy lives on a small island full of resources that lets her produce two goods: x and y. Her production
possibility frontier (constraint) is given by x2 + y2 = 300. Skippy works alone to maximize her utility
which is given by U(x; y) = x2y.
(1) Set up the Lagrangian function for Skippy and solve for x and y. Use your solution to calculate U.
(10 marks)
(2) Carefully graph and label the PPF and Indifference Curve at the optimum. (10 marks)
Now Skippy has the opportunity of trading in the world market. Skippy can trade whatever x and y
she has at prices px and py. To maximize her gains from trade, Skippy needs to follow a 2-step process.
Step 1. First, she maximizes her endowment position (maximize trading line) subject to her PPF, where
the solution to this Lagrange problem (xE, yE) is her production decision and are her endowments she
will use for trade.
Step 2. Second, she maximizes utility subject to the constraint, pxxE + pyyE = pxx + pyy, where x
and y are the quantities she trades for that maximize her utility.
(3) If px = py = $1, please solve the Lagrangian that maximizes her endowments. Then use the endow-
ment value and prices are given in the trading constraint to maximize her utility by the Lagrangian method.
Calculate her utility number. (20 marks)
(4) Give an economic interpretation to each Lagrangian multiplier in the endowment-maximization
problem and the utility-maximization problem in (3). (10 marks)
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


