Question 2 consists of parts a, b, and c -

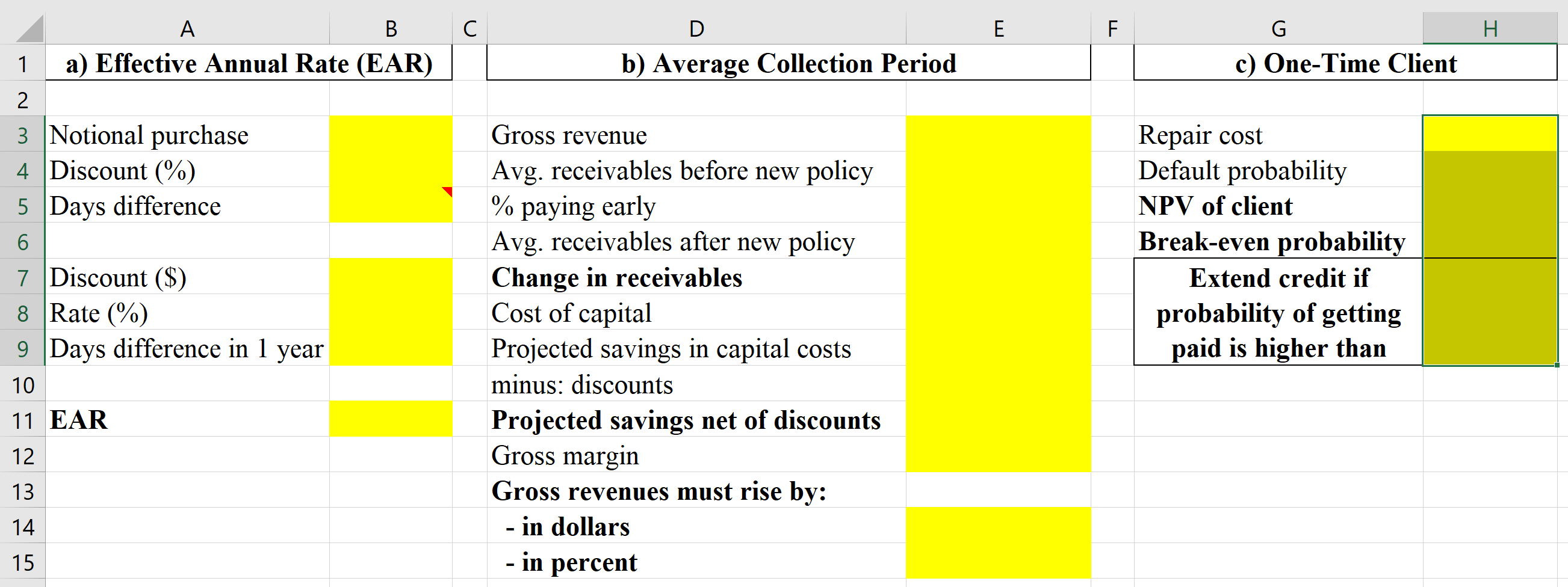
a. Argo sells maintenance services to various private jet operators. For these, it demands payment within 15 days. Argo is considering changing this policy to 1.1%/5, net 15. What is the implicit effective annual rate in this payment policy?

b. Argo's maintenance service business grosses some $33M per year before discounts and its average days receivable is 20 (unlike the overall business where this number is ~15). If 20% of Argo's clients opt to pay earlier and get the 1.1% discount, what will be the change in the service business's receivables? If Argo's cost of capital is 6%, what are the projected savings of this change in policy? If Argo's gross margin is 33%, by how much will gross dollar revenues have to rise to offset the loss from discounts? In percent?

c. A new client from out of town is quoted $5,500 for a repair. The service people ask you to approve this. You do a quick check on the client and assess a 10% default risk. What is the NPV of the client? What is the break-even probability? What is the minimum probability of collecting for you to approve the service?

IMPORTANT: PLEASE SHOW FORMULAS USED TO CALCULATE INSIDE THE FORMULAS ( I ONLY NEED TO COMPLETE THE INFORMATION IN THE YELLOW CELLS)

E F G D b) Average Collection Period c) One-Time Client A B 1 a) Effective Annual Rate (EAR) 2 3 Notional purchase 4 Discount (%) 5 Days difference 6 7 Discount ($) 8 Rate (%) 9 Days difference in 1 year 10 11 EAR Gross revenue Avg. receivables before new policy % paying early Avg. receivables after new policy Change in receivables Cost of capital Projected savings in capital costs minus: discounts Projected savings net of discounts Gross margin Gross revenues must rise by: - in dollars - in percent Repair cost Default probability NPV of client Break-even probability Extend credit if probability of getting paid is higher than 12 13 14 15 E F G D b) Average Collection Period c) One-Time Client A B 1 a) Effective Annual Rate (EAR) 2 3 Notional purchase 4 Discount (%) 5 Days difference 6 7 Discount ($) 8 Rate (%) 9 Days difference in 1 year 10 11 EAR Gross revenue Avg. receivables before new policy % paying early Avg. receivables after new policy Change in receivables Cost of capital Projected savings in capital costs minus: discounts Projected savings net of discounts Gross margin Gross revenues must rise by: - in dollars - in percent Repair cost Default probability NPV of client Break-even probability Extend credit if probability of getting paid is higher than 12 13 14 15