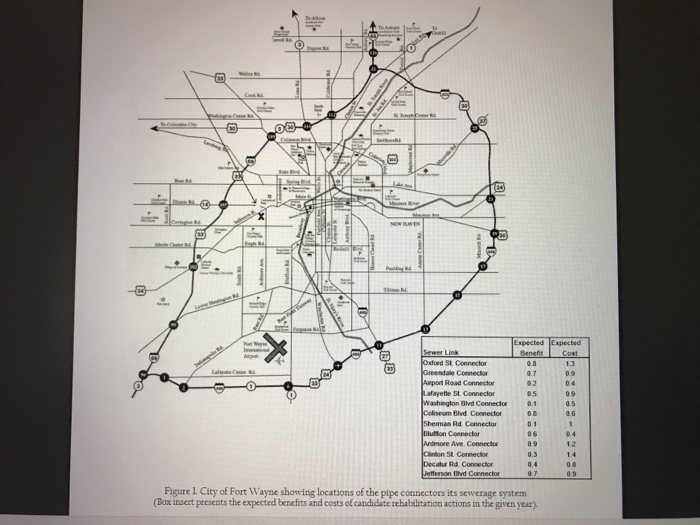
QUESTION 2 (Discrete variable Optimization, Unconstrained). Tool to use: Knapsack or binary programming. (A Sample Excel Solver application, is provided on Blackboard, for your convenience) As most sewer pipes in developed countries approach the end of their service lives, there is increasing danger of pipe failures, leakages, and violent explosions due to methane gas accumulations. Therefore, there exists an urgent need to carry out rehabilitation in order to extend sewer pipe service lives. However, most cities are finding that budgets are limited and therefore not all sewer pipes can be rehabilitated with available budgets. The sewerage system for the City of Fort Wayne (Figure I) consists of 12 major connecting pipe ctions along the streets shown in the figure. It is planned to carry out rehabilitation in 2016 on the connector pipes in order to extend their service life, and to improve their condition and performance. However, due to budgetary limitations, not all the connector pipes can be rehabilitated The table insert in Figure 1 shows, for each connector, the anticipated overall benefits (in terms of enhanced pipe durability and condition, customer satisfaction, etc.) and costs (in millions of dollars) if the rehabilitation is carried out. The rehabilitation budget for that year is $5 M (i.e. 5 units of cost) and the city's mayor seeks to maximize the total benefits, under the given budget, to be earned due to the rehabilitation projects selected in that year As a consultant for the City of Fort Wayne, you are advising the city to identify the optimal solution ch pipes must be rehabilitated and which must not, in order to satisfy the objective and constraints) (a) Write the stated objective in mathematical notation he constraints in mathematical notation. Don't forget the binary choice constraints! (c) Use Solver to solve this problem (i.e, find the optimal solution) (d) Adding a political constraint: Now assume that the city mayor requests that rehabilitation work on the erman Road Connector should definitely be among those to be carried out, irrespective of its costs or e this additional constraint in mathematical notation. (e) Use Solver to determine the new optimal solution due to the addition of this political constraint and discuss how the solution changed compared to that in ( (t) For each of (C) and (e). attach a 1-page output printout of the Solver output solution