Question 2: Explain how the equations for the shadow are found in this example and how this helps find the y-limits and x-limits of the triple integral. Note that the equation of the shadow is not given here and must be found. Do not just state the equation of the shadow for this. Generally, the equation(s) for the shadow can be found based this way, though sometimes you have to be careful about this.

Hint 1: Read Example 4 (p. 927 - 928).

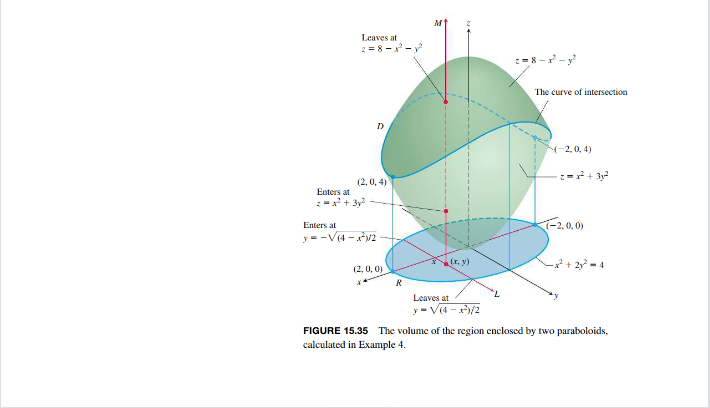
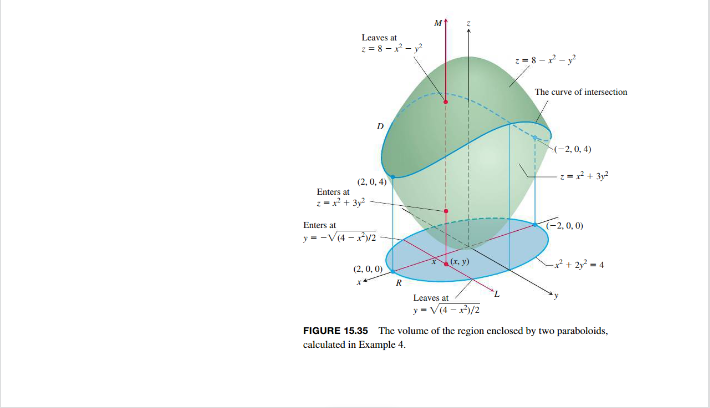
15.5 Triple Integrals in Rectangular Coordinates 927 J. [a - xx - {n - x dx = -6 (1 - x) = 1. Next we set up and evaluate a triple integral over a more complicated region. EXAMPLE 4 Find the volume of the region / enclosed by the surfaces z = x3 + 3y2 and z = 8 - x - yz. Solution The volume is V = dz dy dx. the integral of F(x, y, z) = 1 over D. To find the limits of integration for evaluating the integral, we first sketch the region. The surfaces (Figure 15.35) intersect on the elliptical cylinder x' + 3y' = 8 - x - y' or x + 2y- = 4,z > 0. The boundary of the region R, the projection of D onto the xy-plane, is an ellipse with the same equation: x' + 2y = 4. The "upper" boundary of R is the curve y = V(4 - x)/2. The lower boundary is the curve y = - V(4 - x)/2. Now we find the z-limits of integration. The line My passing through a typical point (x, y) in R parallel to the z-axis enters D atz = x7 + 3y' and leaves at z = 8 - x - y.Leaves at 238-7-12 - v The curve of intersection D mmm. (- 2. 0. 4) (2, 0, 4) Enters at Enters at 7-2,0, 0) 1- -V(4-x-V2 (2, 0, 0) -x- + 2-4 R Leaves at - V(4-13)/2 FIGURE 15.35 The volume of the region enclosed by two paraboloids, calculated in Example 4.928 Chapter 15 Multiple Integrals Next we find the y-limits of integration. The line Z through (x. y) that lies parallel to the y-axis enters the region R when y - -V(4 - x3)/2 and leaves when y = V (4 - x )/2. Finally we find the x-limits of integration. As L sweeps across R, the value of x varies from x = -2 at (-2, 0. 0) to x = 2 at (2. 0, 0). The volume of D is v = Integrand is 1 when computing volume. V14-F/2 LL. dz dy dx Substitute limits of integration. 4-17/2 LL. (8 - 212 - 4y= ) dy dx Integrate over z and evaluate. dx Integrate over y Evaluate. = 8TV/2. After integration with the substitution x = 2 xin a Average Value of a Function in Space The average value of a function F over a region D in space is defined by the formula Average value of F over D = volume of D F dv . (2) For example, if F(x, y.=) = Vx + y + 2, then the average value of F over D is the average distance of points in D from the origin. If F(x, y, 2) is the temperature at (x, y, 2) on a solid that occupies a region D in space, then the average value of F over D is the average temperature of the solid.EXAMPLE 5 Find the average value of F(x, y. 2) = 12 throughout the cubical region D bounded by the coordinate planes and the planes x = 2, y = 2, and z = 2 in the first octant. Solution We sketch the cube with enough detail to show the limits of integration (Figure 15.36). We then use Equation (2) to calculate the average value of F over the cube. The volume of the region D is (2)(2)(2) = 8. The value of the integral of F over the cube is -2 xyz dx dy dz 2yz dy dz. 12 = 8. With these values, Equation (2) gives Average value of wyz dV = (8) = 1. xyz over the cube volume cube FIGURE 15.36 The region of integration In evaluating the integral, we chose the order dx dy de, but any of the other five possible in Example 5. orders would have done as well