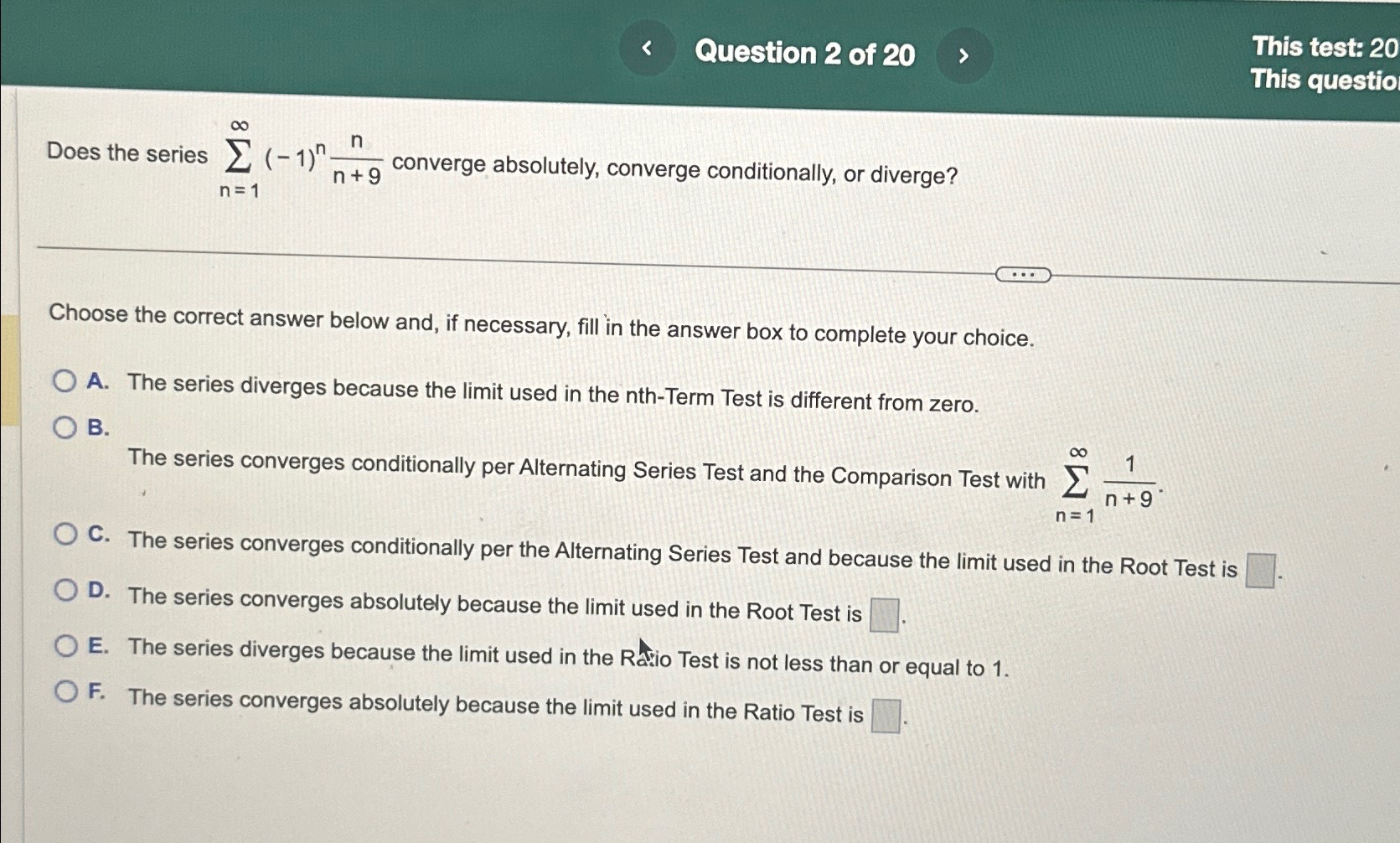
Question $2$ of $20$

This test: $20$

This questio

Does the series ${\displaystyle \underset{n=1}{\overset{}{}}}(-1{)}^n\frac{n}{n+9}$ converge absolutely$,$ converge conditionally, or diverge?

Choose the correct answer below and, if necessary, fill in the answer box to complete your choice.

A$.$ The series diverges because the limit used in the nth$-$Term Test is different from zero.

B$.$ The series converges conditionally per Alternating Series Test and the Comparison Test with ${\displaystyle \underset{n=1}{\overset{}{}}}\frac{1}{n+9}.$

C$.$ The series converges conditionally per the Alternating Series Test and because the limit used in the Root Test is

D$.$ The series converges absolutely because the limit used in the Root Test is

E$.$ The series diverges because the limit used in the Ratio Test is not less than or equal to $1.$

F$.$ The series converges absolutely because the limit used in the Ratio Test is