Question:
20 Use the paragraph below to answer questions :
Breast cancer is the most common malignancy in women worldwide. Tea has anticarcinogenic effects against breast cancer in laboratory studies. However, epidemiologic evidence that tea protects against breast cancer has been inconsistent. A study was conducted in Southeast China between 2004 and 2005. The cases were 1009 female patients aged 20-87 years with histologically confirmed breast cancer. The 1009 age-matched controls were healthy women randomly recruited from breast disease clinics. Information on duration, frequency, quantity, preparation, type of tea consumption, diet and lifestyle were collected by face-to-face interview using a validated and reliable questionnaire. Conditional logistic regression analyses were used to estimate odds ratios (ORs) and associated 95% confidence intervals. Compared with non-tea drinkers, green tea drinkers tended to reside in urban areas, have better education and have higher consumption of coffee, alcohol, soy, vegetables and fruits. After adjusting established and potential confounders, green tea consumption was associated with a reduced odds of breast cancer. The ORs were 0.87 (0.73-1.04) in women consuming 1-249 g of dried green tea leaves per annum, 0.68 (0.54-0.86) for 250-499 g per annum, 0.59 (0.45-0.77) for 500-749 g per annum and 0.61 (0.48-0.78) for >or=750 g per annum, with a statistically significant test for trend (P
Which OR for the association of dried green tea leaves (which amount) presented by the study shows the strongest association between green tea and breast cancer?
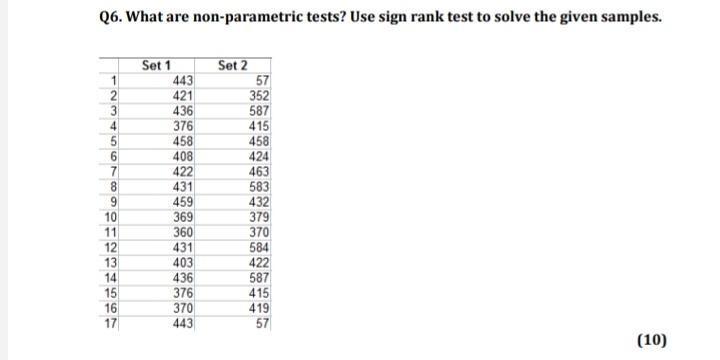
Q6. What are non-parametric tests? Use sign rank test to solve the given samples. Set 1 Set 2 443 57 421 352 436 587 376 415 458 458 408 424 422 463 431 583 459 432 369 379 11 360 370 12 431 584 13 403 422 14 436 587 15 376 415 16 370 419 17 443 57 (10)Q6. What are non-parametric tests? Use sign rank test to solve the given samples. Set 1 Set 2 443 57 421 352 436 587 376 415 458 458 408 424 422 463 431 583 459 432 369 379 11 360 370 12 431 584 13 403 422 14 436 587 15 376 415 16 370 419 17 443 57 (10)2. Contour of bivariate Gaussian. Sketch the contour defined by f(x, y) = 0.06, where f(x, y) is the bivariate normal density with (a) Ax = 1, My = 2,02 = 03 = 1 and pry = 0. (b) Hz = 0, My = 0, 03 = of = 1 and Pry = 0.2. (c) #x = 0, My = 0,02 = 07 = 1 and Pxy = 0.8. (d) Ax = 0, My = 0,02 = 4, 0% = 1 and pry = 0.8. Here, o2 := VarX, o2 := VarY, and the correlation coefficient is defined as Pry := E(X -HI) ( Y-Hy) What is the distribution of X - Y, when (X, Y) has each of the bivariate distributions given above?2. Contour of bivariate Gaussian. Sketch the contour defined by f(x, y) = 0.06, where f(x, y) is the bivariate normal density with (a) Ax = 1, My = 2,02 = 03 = 1 and pry = 0. (b) Hz = 0, My = 0, 03 = of = 1 and Pry = 0.2. (c) #x = 0, My = 0,02 = 07 = 1 and Pxy = 0.8. (d) Ax = 0, My = 0,02 = 4, 0% = 1 and pry = 0.8. Here, o2 := VarX, o2 := VarY, and the correlation coefficient is defined as Pry := E(X -HI) ( Y-Hy) What is the distribution of X - Y, when (X, Y) has each of the bivariate distributions given above?Question 1 What is a non-parametric test? How is it different then a parametric test? What are some reasons that we might want to use a non-parametric test instead of a parametric test? QUESTION 2 What are the two different version of R-Squared? What is the difference between the two of them? (3)Question 1 What is a non-parametric test? How is it different then a parametric test? What are some reasons that we might want to use a non-parametric test instead of a parametric test? QUESTION 2 What are the two different version of R-Squared? What is the difference between the two of them? (3)8:24 46:38 Exit Which is true about the difference between the statistical power of parametric vs. non- parametric tests (i.e., the probability that each type of test will detect a significant effect when one exists)? Parametric tests will definitely have more statistical power than non- parametric tests only if the data meet the assumptions of parametric tests (such as having a normally distributed sampling distribution) Parametric tests always have more statistical power than non-parametric tests Non-parametric tests always have more statistical power than parametric tests No difference; parametric and non- parametric tests have equivalent statistical power for any given set of data 11. When running a non-parametric test on8:24 46:38 Exit Which is true about the difference between the statistical power of parametric vs. non- parametric tests (i.e., the probability that each type of test will detect a significant effect when one exists)? Parametric tests will definitely have more statistical power than non- parametric tests only if the data meet the assumptions of parametric tests (such as having a normally distributed sampling distribution) Parametric tests always have more statistical power than non-parametric tests Non-parametric tests always have more statistical power than parametric tests No difference; parametric and non- parametric tests have equivalent statistical power for any given set of data 11. When running a non-parametric test on