Question 3 please

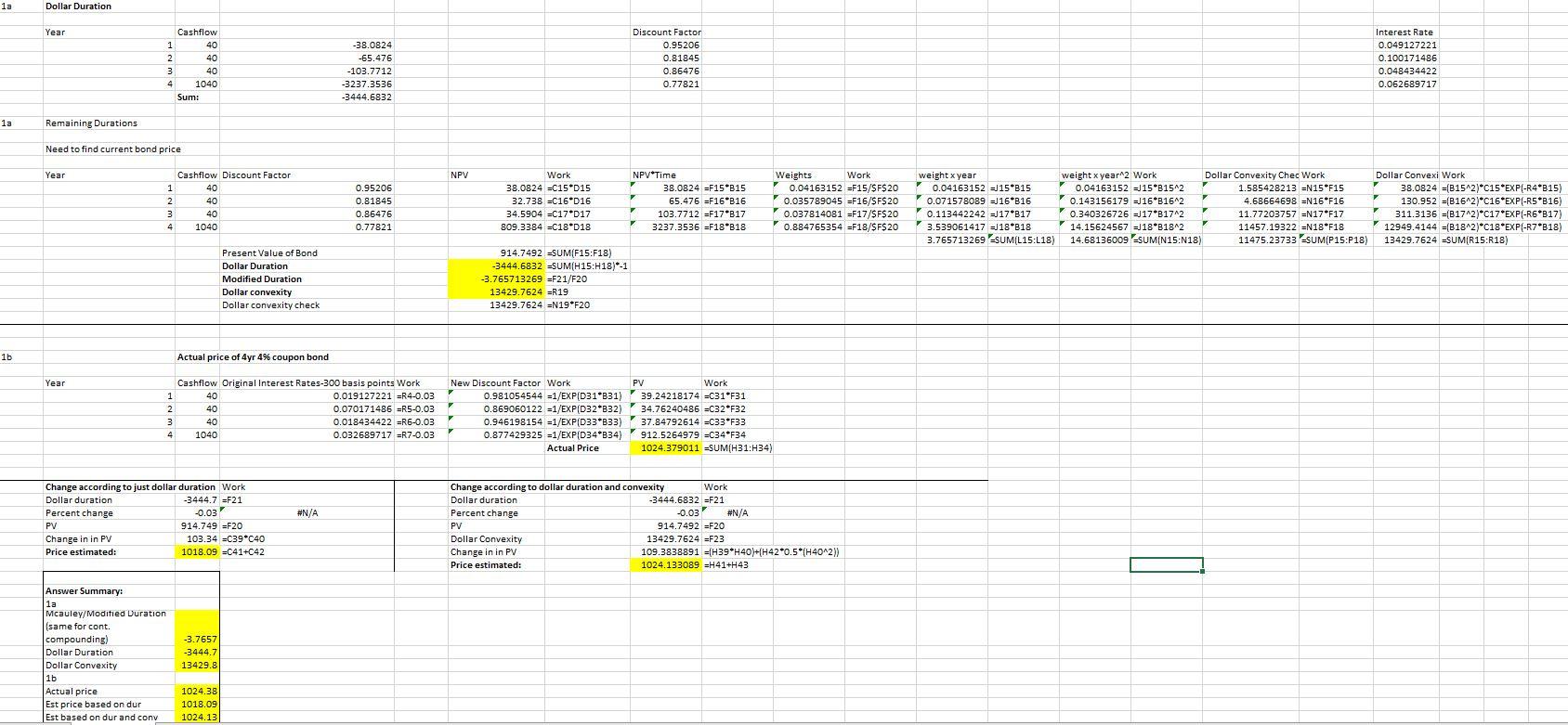
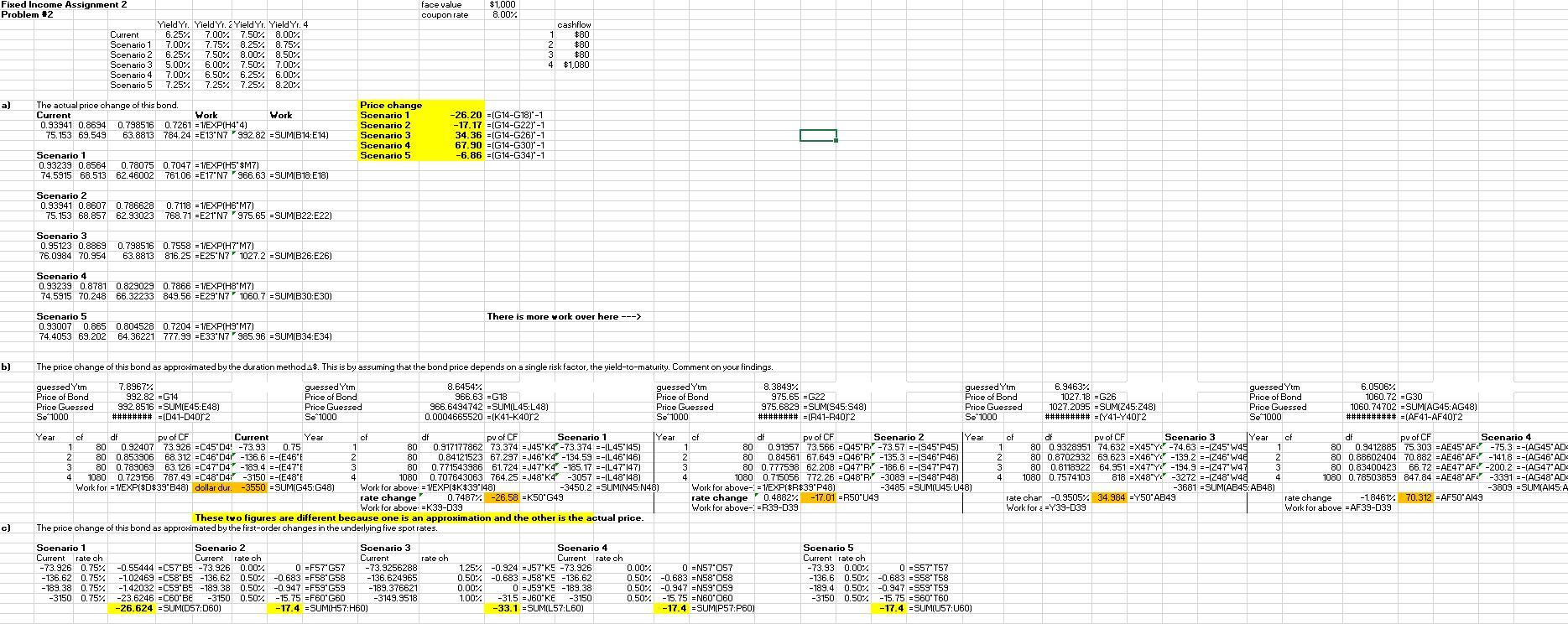
1. Risk Measurement, Dollar Duration, Converily, and Macaulay Duration - 30 points The following discount factors are given: B(0,1)= 0.95206 B(0, 2) = 0.81845 B(0,3)=0.86476 B(0,4)= 0.77821 As a reminder, S Duration, for a bond with continuously compounded yields is: T As - Key =1 (a) Using continuous compounding, calculate the duration D(y), modified duration MD(y),the dollar duration As, and the dollar convexity T's of a 4 year 4% annual coupon bond with face value $1,000. (b) If there is a 300 basis point downward shift in the continuously compounded zero- yield curve (assume all shifts in the continuously compounded zero yield curve are uniform) calculate the following: i. The actual price of this 4-year, 4% coupon bond; ii. The price of the 4 year bond as estimated by As alone; iii. The price of the 4 year bond as estimated by both As and I's. 2. Risk Measurement, Duration - 30 points Dollar duration and convexity are used to characterize and to control the riskiness of fixed income securities. However, several examples were presented in the lectures to exhibit the limitations of these measures. One way we might attempt to improve these measures is by making them more robust to non-uniform shifts in the term structure. For a fixed income security that makes annual payments over four years, 4 P(R1, R2, R3, R)-Ke-R, L=1 where Ris short for the spot rate R(0,1), we can perform a Taylor expansion to arrive at an expression relating the change in price of the bond to changes in the zero coupon term structure by -. (1) aR Consider an 8% coupon bond maturing in four years with a face value of $1000. You are given the following information about the current state of the continuously compounded zero yield curve, and four possible scenarios that might occur instantaneously. Yield Yr. 1 Yield Yr. 2 Yield Yr. 3 Yield Yr. 4 Current 6.25% 7.00% 7.50% 8.00% Scenario 1 7.00% 7.75% 8.25% 8.75% Scenario 2 6.25% 7.50% 8.00% 8.50% Scenario 3 5.00% 6.00% 7.50% 7.00% Scenario 4 7.00% 6.50% 6.25% 6.00% Scenario 5 7.25% 7.25% 7.25% 8.20% For each scenario, compute the following: (a) The actual price change of this bond. (b) The price change of this bond as approximated by the duration method As. This is by assuming that the bond price depends on a single risk factor, the yield to maturity. Comment on your findings. (e) The price change of this bond as approximated by the first-order changes in the underlying five spot rates. 3. Risk Management, Duralion, and Conuerity - 40 points Consider the following three securities: Security A is a 2 year zero which matures two years from today, and pays $1 at maturity; Security B is a 3 year zero which matures three years from today, and pays $1 at maturity; Security C is a 1-year forward contract which matures one year from today, and delivers a 1-year zero (with face value $1) at maturity. My portfolio currently consists of a long position of 5,000 units of security B and a short position (liability) of 3,000 units of security A. Suppose the only securities I can currently trade (buy/sell) are Security A and Security C. The current term structure based on zero coupon bonds (with 1, 2, 3, and 4 year maturity from today) in annualized rates with continuous compounding is: R(0,1)= 3% R(0,2) = 5% R(0, 3) = 6% R(0,4)= 6.5% 2 (a) What are the current value, the dollar duration and the convexity of my portfolio? Interpret the dollar duration and the convexity numbers (i.e. for a 100 basis point parallel increase in the term structure, what do the duration and convexity numbers say?). (b) Without changing the value of my portfolio (found in part (a)), what do I have to do now (i.e., if anything, long/short what? how much?) to achieve a dollar duration of zero for my portfolio? (Suppose I don't care about convexity.) (e) How long is the hedge in part (b) (i.e., the zero dollar duration position) good for? Why? Explain. 1a Dollar Duration Year Cashflow 1 40 2 40 3 40 4 4 1040 Sum: -38.0824 -65.476 -103.7712 -3237.3536 -3444.6832 Discount Factor 0.95206 0.81845 0.86476 0.77821 Interest Rate 0.049127221 0.100171486 0.048434422 0.062689717 1a Remaining Durations Need to find current bond price Year NPV 1 2 3 4 Cashflow Discount Factor 40 40 40 1040 0.95206 0.81845 0.86476 0.77821 Work 38.0824 =C15D15 32.738 =C16*D16 34.5904 =C17*D17 809.3384 =C18D18 NPV Time 38.0824 =F15*B15 65.476 =F16*816 103.7712 =F17B17 3237.3536 =F18*B18 Weights Work 0.04163152 =F15/$F$20 0.035789045 =F16/$F$20 0.037814081 =F17/$F$20 0.884765354 =F18/$F$20 weight x year 0.04163152 =J15*B15 0.071578089 - 16*B16 0.113442242 = 17*B17 3.539061417 18B18 3.765713269 SUM{L15:L18) weight x year 2 Work Dollar Convexity Chec Work 0.04163152 -J15*31542 1.585428213 EN15 F15 0.143156179 -J16*B16-2 4.68664698 =N16*F16 0.340326726 =17*B1742 11.77203757 =N17F17 14.15624567 = 18*81842 11457.19322 =N18F18 14.68136009 -SUM(N15:N18) 11475.23733 SUM(P15:P18) Dollar Convexi Work 38.0824 =(B1542)*C15*EXP(-R4*815) 130.952 =(B16-2)*C16*EXP(-R5*816) 311.3136 =(81742)*C17*EXP(-R6*B17) 12949.4144 =(B1842)*C18*EXP(-R7*818) 13429.7624 SUM(R15:R18) Present Value of Bond Dollar Duration Modified Duration Dollar convexity Dollar convexity check 914.7492 -SUM(F15:F18) -3444.6832 =SUM(H15:H18)-1 -3.765713269 =F21/F20 13429.7624 =R19 13429.7624 =N19F20 1b Actual price of 4yr 4% coupon bond Year 1 2 3 4 Cashflow Original Interest Rates-300 basis points Work 40 0.019127221 =R4-0.03 40 0.070171486 =R5-0.03 40 0.018434422 =R6-0.03 1040 0.032689717 =R7-0.03 New Discount Factor Work PV Work 0.981054544 =1/EXP(D31*B31) 39.24218174 C31F31 0.869060122 =1/EXP(D32 B32) 34.76240486 =C32*F32 0.946198154 =1/EXP(D33*833) 37.84792614 =C33*F33 0.877429325 =1/EXP(D34*834) 912.5264979 -C34*F34 * = Actual Price 1024.379011 SUM(H31:34) Change according to just dollar duration Work Dollar duration -3444.7 =F21 Percent change -0.03 PV 914.749 =F20 Change in in PV 103.34 =C39C40 Price estimated: 1018.09 =C41+C42 #N/A #N Change according to dollar duration and convexity Work Dollar duration -3444.6832 =F21 Percent change -0.03 #N/A PV 914.7492 =F20 Dollar Convexity 13429.7624 =F23 Change in in PV 109.3838891 =(H39*H40)+(H42*0.5*(H4042) Price estimated: 1024 133089 =H41+H43 Answer Summary: 1a Mcauley/Modified Duration (same for cont. compounding) Dollar Duration Dollar Convexity 1b Actual price Est price based on dur Est based on dur and conv -3.7657 -3444.7 13429.8 1024.38 1018.09 1024.13 face value coupon rate $1,000 8.00% Fixed Income Assignment 2 Problem #2 Yield Yr. Yield Yr. 2 Yield Yr. Yield Yr. 4 Current 6.25% 7.00% 7.50% 8.00% Scenario 1 7.00% % 7.75% 8.25% 8.75% Scenario 2 6.25%. 7.50% 8.00% 8.50% Scenario 3 5.00% 6.00% 7.50% 7.00% Scenario 4 7.00% 6.50% 6.25%. 6.00% Scenario 5 7.25% 5 . 7.25% 7.25%. 8.20% cashflow 1 $80 2 $80 3 $80 4 4 $1,080 a) The actual price change of this bond. Current Work Work 0.93941 0.8694 0.798516 0.7261 -1/EXP(H4'4) 75.153 69.549 63.8813 784.24 =E13 N7 992.82 = SUM(B14:E14) Price change Scenario 1 Scenario 2 Scenario 3 3 Scenario 4 Scenario 5 -26.20 = (G14-G18)-1 -17.17 =(G14-G22)-1 34.36 = (G14-G26)*-1 67.90 = (G14-G30)-1 -6.86 = (G14-G34)-1 Scenario 1 0.93239 0.8564 0.78075 0.7047 = 1/EXP(H5'$M7) 74.5915 68.513 62.46002 761.06 =E17'N7 966.63 = SUM(B18:E18) Scenario 2 0.93941 0.8607 0.786628 0.7118 = 1/EXP(H6'M7) 1/ 75.153 68.857 62.93023 768.71 =E21N7 975.65 - SUM(B22:E22) Scenario 3 0.95123 0.8869 0.798516 0.7558 = 1/EXP(H7+M7) = /) 76.0984 70.954 63.8813 816.25 =E25'N7' 1027.2 -SUM(B26:E26) ' = Scenario 4 4 0.93239 0.8781 0.829029 0.7866 = 1/EXP(H8*M7) 74.5915 70.248 66.32233 849.56 =E29 N71060.7 = SUM(B30:E30) There is more work over here ---> Scenario 5 5 0.93007 0.865 0.804528 0.7204 = 1/EXP(H9"M7) 74.4053 69.202 64.36221 777.99 =E33'N7985.96 = SUM(B34:E34) b) The price change of this bond as approximated by the duration method 4$. This is by assuming that the bond price depends on a single risk factor, the yield-to-maturity. Comment on your findings. , guessed Ytm Price of Bond Price Guessed Se 1000 7.8967% 992.82 =G14 992.8516 = SUME45:E48) ######## = (D41-D402 guessed Ytm Price of Bond Price Guessed Se 1000 8.6454% 966.63 =G18 966.6494742 =SUM(L45:L48) 0.0004665520 = (K41-K402 guessed Ytm Price of Bond Price Guessed Se 1000 8.3849% 975.65 =G22 975.6829 - SUM(S45:S48) ######## -(R41-R4082 guessed Ytm Price of Bond Price Guessed Se 1000 6.9463% 1027.18 =G26 1027.2095 = SUMIZ45:248) ######### = (Y41-Y4052 guessed Ytm Price of Bond Price Guessed Se 1000 6.0506% 1060.72 =G30 1060.74702 =SUMAG45:AG48) ########## =(AF41-AF4012 Year of df py of CF Current Year of df py of CF Scenario 1 Year 1 80 0.92407 73.926 =C45'D4! -73.93 0.75 1 80 0.917177862 73.374 - J45 K4 -73.374 =-(L45'145) 2 80 0.853906 68.312 =C46'041 -136.6 =-(E46' 2 80 0.84121523 67.297 = J46'K4-134.59 =-(L46'146) 3 3 80 0.789069 63.126 =C47"04" -189.4 =-(E47" ='( 3 80 0.771543986 61.724 - J47"K4 -185.17 =-(L47*147) 4 1080 0.729156 787.49 =C48'D4: -3150 --(E48' 4 1080 0.707643063 764.25 = J48 K4-3057 =-(L48'148) Work for = 1/EXP($D$39'B48) dollar dur. -3550 = SUM(G45:G48) Work for above = 1/EXP($K$39*148) -3450.2 = SUM(N45:N48) rate change' 0.7487% -26.58 EK50'G49 Work for above. =K39-039 These two figures are different because one is an approximation and the other is the actual price. The price change of this bond as approximated by the first-order changes in the underlying five spot rates. of df py of CF Scenario 2 Year 1 80 0.91957 73.566 =Q45'R' -73.57 =-(S45'P45) 2 80 0.84561 67.649 =Q46'R-135.3 =-(S46'P46) 3 80 0.777598 62.208 =Q47'R-186.6 --(S47'P47) 4 1080 0.715056 772.26 =Q48'R' -3089 =-(S48'P48) Work for above- = 1/EXP($R$39'P48) -3485 - SUM(U45:048) rate change 0.4882% -17.01 = R50'049 Work for above- =R39-039 ch df pv of CF Scenario 3 Year of di py of CF Scenario 4 1 80 0.9328951 74.632 =X45'Y2 -74.63 =-(Z45'W45 1 80 0.9412885 75.303 = AE45'AF -75.3 =-(AG45'AD 2 80 0.8702932 69.623 =X46'Y-139.2 --(246'W4 2 80 0.88602404 70.882 -AE46'AF-141.8 --(AG46'AD 3 80 0.8118922 64.951 =X47"Y2 -194.9 =-(247"W47 3 80 0.83400423 66.72 = AE47'AF!-200.2 --(AG47"AD == 4 1080 0.7574103 818 =X48"Y! -3272 --1248 W48 4 1080 0.78503859 847.84 EAE48*AF -3391 =-(AG48*AD -3681 ESUMAB45:AB48) -3809 = SUM(A145:A rate char -0.9505%. 34.984 -Y50'AB49 rate change -1.8461% 70.312 - AF50 A149 Work for a =Y39-039 Work for above =AF39-039 c) Scenario 1 Scenario 2 Scenario 3 Current rate ch Current rate ch Current ratech -73.926 0.75%. -0.55444 =C57B5 -73.926 0.00% 0 =F57"G57 -73.9256288 - 136.62 0.75%. .-1.02469 =C58'B5 -136.62 0.50% -0.683 =F58'G58 -136.624965 -189.38 0.75%. -1.42032 =C59'B5 -189.38 0.50% -0.947 =F59'G59 -189.376621 -3150 0.75% -23.6246 =C60'BE-3150 0.50% -15.75 =F60"G60 %. % -3149.9518 -26.624 =SUM(D57:060) -17.4 = SUM(H57:H60) Scenario 4 Current rate ch 1.25% -0.924 = J57"K5 -73.926 0.00% 0 =N57'057 0.50% -0.683 = 358 K5 -136.62 0.50% -0.683 =N58'058 0.00% 0 = J59'K5 -189.38 0.50% -0.947 =N59'059 1.00% -31.5 = 60'KE -3150 0.50% -15.75 +N60'060 = -33.1 = SUM(L57:L60) -17.4 = SUM(P57:P60) :) Scenario 5 Current rate ch -73.93 0.00% 0 =S57' T57 -136.6 0.50% -0.683 = S58'T58 -189.4 0.50% -0.947 =559*759 % -3150 0.50% -15.75 -560'T60 -17.4 =SUM(U57:U60) = 1. Risk Measurement, Dollar Duration, Converily, and Macaulay Duration - 30 points The following discount factors are given: B(0,1)= 0.95206 B(0, 2) = 0.81845 B(0,3)=0.86476 B(0,4)= 0.77821 As a reminder, S Duration, for a bond with continuously compounded yields is: T As - Key =1 (a) Using continuous compounding, calculate the duration D(y), modified duration MD(y),the dollar duration As, and the dollar convexity T's of a 4 year 4% annual coupon bond with face value $1,000. (b) If there is a 300 basis point downward shift in the continuously compounded zero- yield curve (assume all shifts in the continuously compounded zero yield curve are uniform) calculate the following: i. The actual price of this 4-year, 4% coupon bond; ii. The price of the 4 year bond as estimated by As alone; iii. The price of the 4 year bond as estimated by both As and I's. 2. Risk Measurement, Duration - 30 points Dollar duration and convexity are used to characterize and to control the riskiness of fixed income securities. However, several examples were presented in the lectures to exhibit the limitations of these measures. One way we might attempt to improve these measures is by making them more robust to non-uniform shifts in the term structure. For a fixed income security that makes annual payments over four years, 4 P(R1, R2, R3, R)-Ke-R, L=1 where Ris short for the spot rate R(0,1), we can perform a Taylor expansion to arrive at an expression relating the change in price of the bond to changes in the zero coupon term structure by -. (1) aR Consider an 8% coupon bond maturing in four years with a face value of $1000. You are given the following information about the current state of the continuously compounded zero yield curve, and four possible scenarios that might occur instantaneously. Yield Yr. 1 Yield Yr. 2 Yield Yr. 3 Yield Yr. 4 Current 6.25% 7.00% 7.50% 8.00% Scenario 1 7.00% 7.75% 8.25% 8.75% Scenario 2 6.25% 7.50% 8.00% 8.50% Scenario 3 5.00% 6.00% 7.50% 7.00% Scenario 4 7.00% 6.50% 6.25% 6.00% Scenario 5 7.25% 7.25% 7.25% 8.20% For each scenario, compute the following: (a) The actual price change of this bond. (b) The price change of this bond as approximated by the duration method As. This is by assuming that the bond price depends on a single risk factor, the yield to maturity. Comment on your findings. (e) The price change of this bond as approximated by the first-order changes in the underlying five spot rates. 3. Risk Management, Duralion, and Conuerity - 40 points Consider the following three securities: Security A is a 2 year zero which matures two years from today, and pays $1 at maturity; Security B is a 3 year zero which matures three years from today, and pays $1 at maturity; Security C is a 1-year forward contract which matures one year from today, and delivers a 1-year zero (with face value $1) at maturity. My portfolio currently consists of a long position of 5,000 units of security B and a short position (liability) of 3,000 units of security A. Suppose the only securities I can currently trade (buy/sell) are Security A and Security C. The current term structure based on zero coupon bonds (with 1, 2, 3, and 4 year maturity from today) in annualized rates with continuous compounding is: R(0,1)= 3% R(0,2) = 5% R(0, 3) = 6% R(0,4)= 6.5% 2 (a) What are the current value, the dollar duration and the convexity of my portfolio? Interpret the dollar duration and the convexity numbers (i.e. for a 100 basis point parallel increase in the term structure, what do the duration and convexity numbers say?). (b) Without changing the value of my portfolio (found in part (a)), what do I have to do now (i.e., if anything, long/short what? how much?) to achieve a dollar duration of zero for my portfolio? (Suppose I don't care about convexity.) (e) How long is the hedge in part (b) (i.e., the zero dollar duration position) good for? Why? Explain. 1a Dollar Duration Year Cashflow 1 40 2 40 3 40 4 4 1040 Sum: -38.0824 -65.476 -103.7712 -3237.3536 -3444.6832 Discount Factor 0.95206 0.81845 0.86476 0.77821 Interest Rate 0.049127221 0.100171486 0.048434422 0.062689717 1a Remaining Durations Need to find current bond price Year NPV 1 2 3 4 Cashflow Discount Factor 40 40 40 1040 0.95206 0.81845 0.86476 0.77821 Work 38.0824 =C15D15 32.738 =C16*D16 34.5904 =C17*D17 809.3384 =C18D18 NPV Time 38.0824 =F15*B15 65.476 =F16*816 103.7712 =F17B17 3237.3536 =F18*B18 Weights Work 0.04163152 =F15/$F$20 0.035789045 =F16/$F$20 0.037814081 =F17/$F$20 0.884765354 =F18/$F$20 weight x year 0.04163152 =J15*B15 0.071578089 - 16*B16 0.113442242 = 17*B17 3.539061417 18B18 3.765713269 SUM{L15:L18) weight x year 2 Work Dollar Convexity Chec Work 0.04163152 -J15*31542 1.585428213 EN15 F15 0.143156179 -J16*B16-2 4.68664698 =N16*F16 0.340326726 =17*B1742 11.77203757 =N17F17 14.15624567 = 18*81842 11457.19322 =N18F18 14.68136009 -SUM(N15:N18) 11475.23733 SUM(P15:P18) Dollar Convexi Work 38.0824 =(B1542)*C15*EXP(-R4*815) 130.952 =(B16-2)*C16*EXP(-R5*816) 311.3136 =(81742)*C17*EXP(-R6*B17) 12949.4144 =(B1842)*C18*EXP(-R7*818) 13429.7624 SUM(R15:R18) Present Value of Bond Dollar Duration Modified Duration Dollar convexity Dollar convexity check 914.7492 -SUM(F15:F18) -3444.6832 =SUM(H15:H18)-1 -3.765713269 =F21/F20 13429.7624 =R19 13429.7624 =N19F20 1b Actual price of 4yr 4% coupon bond Year 1 2 3 4 Cashflow Original Interest Rates-300 basis points Work 40 0.019127221 =R4-0.03 40 0.070171486 =R5-0.03 40 0.018434422 =R6-0.03 1040 0.032689717 =R7-0.03 New Discount Factor Work PV Work 0.981054544 =1/EXP(D31*B31) 39.24218174 C31F31 0.869060122 =1/EXP(D32 B32) 34.76240486 =C32*F32 0.946198154 =1/EXP(D33*833) 37.84792614 =C33*F33 0.877429325 =1/EXP(D34*834) 912.5264979 -C34*F34 * = Actual Price 1024.379011 SUM(H31:34) Change according to just dollar duration Work Dollar duration -3444.7 =F21 Percent change -0.03 PV 914.749 =F20 Change in in PV 103.34 =C39C40 Price estimated: 1018.09 =C41+C42 #N/A #N Change according to dollar duration and convexity Work Dollar duration -3444.6832 =F21 Percent change -0.03 #N/A PV 914.7492 =F20 Dollar Convexity 13429.7624 =F23 Change in in PV 109.3838891 =(H39*H40)+(H42*0.5*(H4042) Price estimated: 1024 133089 =H41+H43 Answer Summary: 1a Mcauley/Modified Duration (same for cont. compounding) Dollar Duration Dollar Convexity 1b Actual price Est price based on dur Est based on dur and conv -3.7657 -3444.7 13429.8 1024.38 1018.09 1024.13 face value coupon rate $1,000 8.00% Fixed Income Assignment 2 Problem #2 Yield Yr. Yield Yr. 2 Yield Yr. Yield Yr. 4 Current 6.25% 7.00% 7.50% 8.00% Scenario 1 7.00% % 7.75% 8.25% 8.75% Scenario 2 6.25%. 7.50% 8.00% 8.50% Scenario 3 5.00% 6.00% 7.50% 7.00% Scenario 4 7.00% 6.50% 6.25%. 6.00% Scenario 5 7.25% 5 . 7.25% 7.25%. 8.20% cashflow 1 $80 2 $80 3 $80 4 4 $1,080 a) The actual price change of this bond. Current Work Work 0.93941 0.8694 0.798516 0.7261 -1/EXP(H4'4) 75.153 69.549 63.8813 784.24 =E13 N7 992.82 = SUM(B14:E14) Price change Scenario 1 Scenario 2 Scenario 3 3 Scenario 4 Scenario 5 -26.20 = (G14-G18)-1 -17.17 =(G14-G22)-1 34.36 = (G14-G26)*-1 67.90 = (G14-G30)-1 -6.86 = (G14-G34)-1 Scenario 1 0.93239 0.8564 0.78075 0.7047 = 1/EXP(H5'$M7) 74.5915 68.513 62.46002 761.06 =E17'N7 966.63 = SUM(B18:E18) Scenario 2 0.93941 0.8607 0.786628 0.7118 = 1/EXP(H6'M7) 1/ 75.153 68.857 62.93023 768.71 =E21N7 975.65 - SUM(B22:E22) Scenario 3 0.95123 0.8869 0.798516 0.7558 = 1/EXP(H7+M7) = /) 76.0984 70.954 63.8813 816.25 =E25'N7' 1027.2 -SUM(B26:E26) ' = Scenario 4 4 0.93239 0.8781 0.829029 0.7866 = 1/EXP(H8*M7) 74.5915 70.248 66.32233 849.56 =E29 N71060.7 = SUM(B30:E30) There is more work over here ---> Scenario 5 5 0.93007 0.865 0.804528 0.7204 = 1/EXP(H9"M7) 74.4053 69.202 64.36221 777.99 =E33'N7985.96 = SUM(B34:E34) b) The price change of this bond as approximated by the duration method 4$. This is by assuming that the bond price depends on a single risk factor, the yield-to-maturity. Comment on your findings. , guessed Ytm Price of Bond Price Guessed Se 1000 7.8967% 992.82 =G14 992.8516 = SUME45:E48) ######## = (D41-D402 guessed Ytm Price of Bond Price Guessed Se 1000 8.6454% 966.63 =G18 966.6494742 =SUM(L45:L48) 0.0004665520 = (K41-K402 guessed Ytm Price of Bond Price Guessed Se 1000 8.3849% 975.65 =G22 975.6829 - SUM(S45:S48) ######## -(R41-R4082 guessed Ytm Price of Bond Price Guessed Se 1000 6.9463% 1027.18 =G26 1027.2095 = SUMIZ45:248) ######### = (Y41-Y4052 guessed Ytm Price of Bond Price Guessed Se 1000 6.0506% 1060.72 =G30 1060.74702 =SUMAG45:AG48) ########## =(AF41-AF4012 Year of df py of CF Current Year of df py of CF Scenario 1 Year 1 80 0.92407 73.926 =C45'D4! -73.93 0.75 1 80 0.917177862 73.374 - J45 K4 -73.374 =-(L45'145) 2 80 0.853906 68.312 =C46'041 -136.6 =-(E46' 2 80 0.84121523 67.297 = J46'K4-134.59 =-(L46'146) 3 3 80 0.789069 63.126 =C47"04" -189.4 =-(E47" ='( 3 80 0.771543986 61.724 - J47"K4 -185.17 =-(L47*147) 4 1080 0.729156 787.49 =C48'D4: -3150 --(E48' 4 1080 0.707643063 764.25 = J48 K4-3057 =-(L48'148) Work for = 1/EXP($D$39'B48) dollar dur. -3550 = SUM(G45:G48) Work for above = 1/EXP($K$39*148) -3450.2 = SUM(N45:N48) rate change' 0.7487% -26.58 EK50'G49 Work for above. =K39-039 These two figures are different because one is an approximation and the other is the actual price. The price change of this bond as approximated by the first-order changes in the underlying five spot rates. of df py of CF Scenario 2 Year 1 80 0.91957 73.566 =Q45'R' -73.57 =-(S45'P45) 2 80 0.84561 67.649 =Q46'R-135.3 =-(S46'P46) 3 80 0.777598 62.208 =Q47'R-186.6 --(S47'P47) 4 1080 0.715056 772.26 =Q48'R' -3089 =-(S48'P48) Work for above- = 1/EXP($R$39'P48) -3485 - SUM(U45:048) rate change 0.4882% -17.01 = R50'049 Work for above- =R39-039 ch df pv of CF Scenario 3 Year of di py of CF Scenario 4 1 80 0.9328951 74.632 =X45'Y2 -74.63 =-(Z45'W45 1 80 0.9412885 75.303 = AE45'AF -75.3 =-(AG45'AD 2 80 0.8702932 69.623 =X46'Y-139.2 --(246'W4 2 80 0.88602404 70.882 -AE46'AF-141.8 --(AG46'AD 3 80 0.8118922 64.951 =X47"Y2 -194.9 =-(247"W47 3 80 0.83400423 66.72 = AE47'AF!-200.2 --(AG47"AD == 4 1080 0.7574103 818 =X48"Y! -3272 --1248 W48 4 1080 0.78503859 847.84 EAE48*AF -3391 =-(AG48*AD -3681 ESUMAB45:AB48) -3809 = SUM(A145:A rate char -0.9505%. 34.984 -Y50'AB49 rate change -1.8461% 70.312 - AF50 A149 Work for a =Y39-039 Work for above =AF39-039 c) Scenario 1 Scenario 2 Scenario 3 Current rate ch Current rate ch Current ratech -73.926 0.75%. -0.55444 =C57B5 -73.926 0.00% 0 =F57"G57 -73.9256288 - 136.62 0.75%. .-1.02469 =C58'B5 -136.62 0.50% -0.683 =F58'G58 -136.624965 -189.38 0.75%. -1.42032 =C59'B5 -189.38 0.50% -0.947 =F59'G59 -189.376621 -3150 0.75% -23.6246 =C60'BE-3150 0.50% -15.75 =F60"G60 %. % -3149.9518 -26.624 =SUM(D57:060) -17.4 = SUM(H57:H60) Scenario 4 Current rate ch 1.25% -0.924 = J57"K5 -73.926 0.00% 0 =N57'057 0.50% -0.683 = 358 K5 -136.62 0.50% -0.683 =N58'058 0.00% 0 = J59'K5 -189.38 0.50% -0.947 =N59'059 1.00% -31.5 = 60'KE -3150 0.50% -15.75 +N60'060 = -33.1 = SUM(L57:L60) -17.4 = SUM(P57:P60) :) Scenario 5 Current rate ch -73.93 0.00% 0 =S57' T57 -136.6 0.50% -0.683 = S58'T58 -189.4 0.50% -0.947 =559*759 % -3150 0.50% -15.75 -560'T60 -17.4 =SUM(U57:U60) =