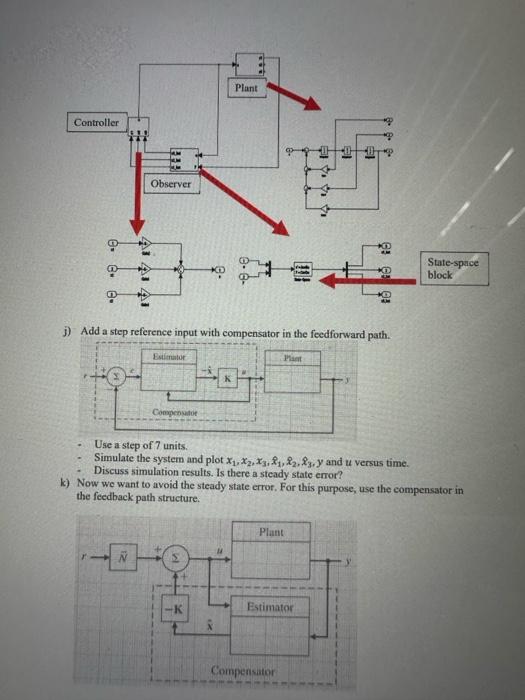
Question 3: x1x2x3=000100010x1x2x3+001uy=[100]x1x2x3 a) Discuss whether the system should be controllable or not. Check your intuition by forming the controllability matrix and checking its rank. b) Assume that all of the state variables can be measured directly; that is, x is measured. Find a state feedback law that places the dominant closed-loop poles of the system so that tr0.1sec and Mp5%. Place the remaining pole of the system 4-5 times farther to the left so that the design specifications are more likely to hold. c) Find the state feedback gains by first matching the coefficients of the desired polynomial and closed-loop characteristic equation. Then check your result by using the Matlab function "acker.m" or "place.m". d) Simulate the closed loop system with a Simullink model. - Model the plant with Simulink integrators and Simulink gains Find the values of these gains from the plant transfer function. Enter the following initial conditions into the simulink integrators - Model the the state feedback controller with a Simulink gain. - Add "time" and "to workspace" blocks. - Simulate the system and plot x1,x2,x3,y and u versus time. - Discuss simulation results. e) Check if this system is observable or not. (Form the observability matrix and check if it is invertable or not.) f) Suppose now that the state variables are not all available for measurement. Design an observer which has poles with magnitudes about 4 times larger than the real parts of the closed-loop system. Determine the observer poles. g) Do coefficient matching to find observer gains. h) Verify the computed observer gains by acker.m. i) Simulate the closed loop system with the observer. - Model the observer with a Simulink "State-Space" block. - Simulate the system and plot x1,x2,x3,x^1,x^2,x^3,y and u versus time. - Discuss simulation results. j) Add a step reference input with compensator in the feedforward path. - Use a step of 7 units. - Simulate the system and plot x1,x2,x3,x1,x2,x3,y and u versus time. - Discuss simulation results. Is there a steady state crror? k) Now we want to avoid the steady state error. For this purpose, use the compensator in the feedback path structure