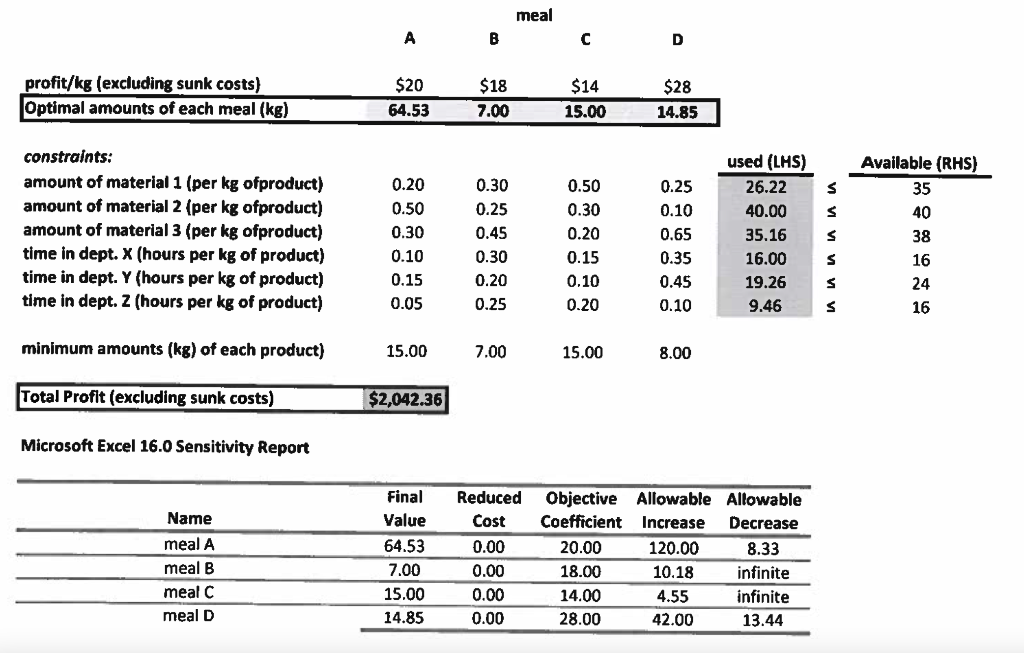
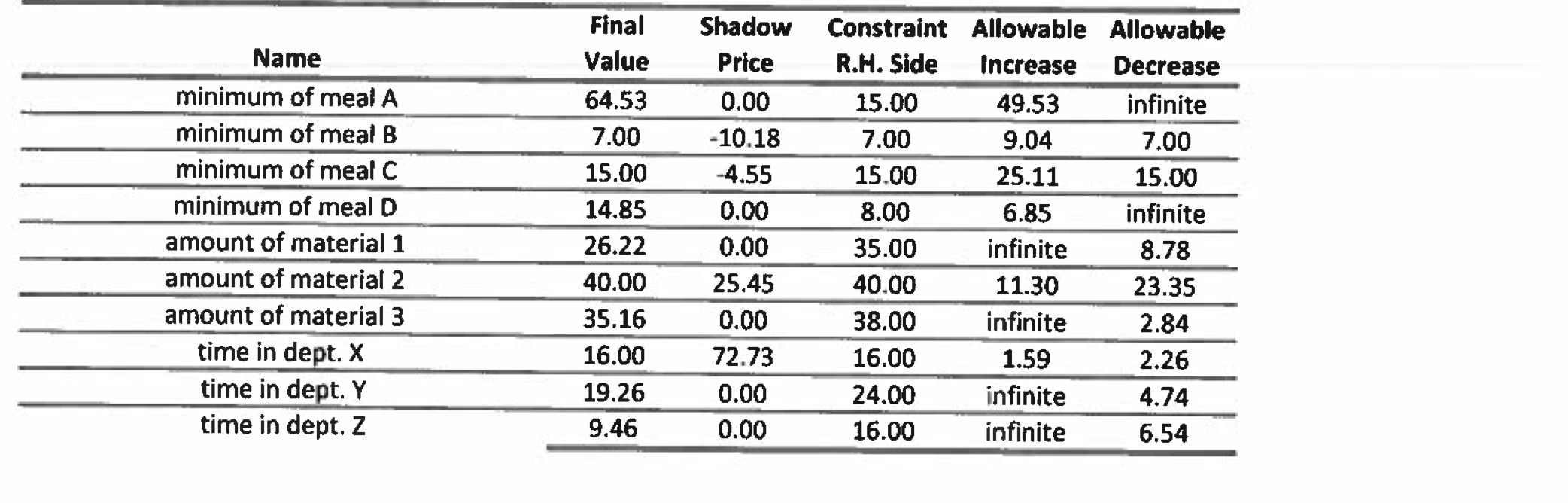
Question 4 (10 marks) A small catering business is expanding its take-out business as a result of the restrictions placed on businesses due to the Covid pandemic. It has decided to prepare 4 different meals using the same 3 food materials but in different proportions, with its customers being allowed to order any size meals that they want. For the next batch of meals that are to be prepared, the attached computer output includes the inputs to the model for this problem and its Solver solution including its sensitivity report: The profits per kg of each different meal, not including any sunk costs The optimal amounts of each meal to produce (in kg's) for its next batch of orders The amounts of each material (in kg's) to go into each kg of each different meal The amounts of time (in hours) required to prepare each kg of each different meal The amounts of each material (in kg's) that are available for producing the next batch of meals The amounts of time (in hours) that are available for producing the next batch of meals in each of the 3 departments the business currently has available The minimum amounts (in kg's) of each type of meal that need to be prepared The amounts of each of the materials and the amounts of time actual used The sensitivity report produced by Solver . . . When answering the following questions, you are to assume that every meal that is prepared is sold and that the following costs are either sunk or relevant as follows: . The material costs per kg are $5 for material 1, $6 for material 2 and $4 for material 3 and that these costs are sunk costs because all the available material must be paid for in advance The labour costs per hour are $6.00 and these costs are relevant costs in that the caterer only pays for the hours needed. When answering each of the following questions, if there is not enough information to answer the question, state that there is 'not enough info' and briefly state why. In addition, if you can answer a question, show any calculations necessary for arriving at your answer. a) What is the optimal amounts of each meal (in kg) that should be produced and what is the total profit (excluding sunk costs) b) Which constraints are binding? c) After producing all the meals, how much of material 3 is left over? d) If the minimum requirement for meal B was decreased by 4kg, what would be the change in total profit (excluding sunk costs)? meal A B profit/kg (excluding sunk costs) Optimal amounts of each meal (kg) $20 64.53 $18 7.00 $14 15.00 $28 14.85 0.20 0.30 s 0.50 s constraints: amount of material 1 (per kg ofproduct) amount of material 2 (per kg ofproduct) amount of material 3 (per kg ofproduct) time in dept. X (hours per kg of product) time in dept. Y (hours per kg of product) time in dept. Z (hours per kg of product) s 0.25 0.45 0.30 0.20 0.25 0.30 0.10 0.15 0.05 0.50 0.30 0.20 0.15 0.10 0.20 used (LMS) 26.22 40.00 35.16 16.00 19.26 9.46 0.25 0.10 0.65 0.35 0.45 0.10 Available (RHS) 35 40 38 16 24 16 $ s s minimum amounts (kg) of each product) 15.00 7.00 15.00 8.00 Total Profit (excluding sunk costs) $2,042.36 Microsoft Excel 16.0 Sensitivity Report Reduced Cost Name meal A meal B meal C meal D Final Value 64.53 7.00 15.00 14.85 0.00 0.00 0.00 0.00 Objective Allowable Allowable Coefficient Increase Decrease 20.00 120.00 8.33 18.00 10.18 infinite 14.00 4.55 infinite 28.00 42.00 13.44 Name minimum of meal A minimum of meat B minimum of meal C minimum of meal D amount of material 1 amount of material 2 amount of material 3 time in dept. X time in dept. Y time in dept. Z Final Value 64.53 7.00 15.00 14.85 26.22 40.00 35.16 16.00 19.26 9.46 Shadow Price 0.00 -10.18 -4.55 0.00 0.00 25.45 0.00 72.73 0.00 0.00 Constraint Allowable Allowable R.H. Side Increase Decrease 15.00 49.53 infinite 7.00 9.04 7.00 15.00 25.11 15.00 8.00 6.85 infinite 35.00 infinite 8.78 40.00 11.30 23.35 38.00 infinite 2.84 16.00 1.59 2.26 24.00 infinite 4.74 16.00 infinite 6.54 Question 4 (10 marks) A small catering business is expanding its take-out business as a result of the restrictions placed on businesses due to the Covid pandemic. It has decided to prepare 4 different meals using the same 3 food materials but in different proportions, with its customers being allowed to order any size meals that they want. For the next batch of meals that are to be prepared, the attached computer output includes the inputs to the model for this problem and its Solver solution including its sensitivity report: The profits per kg of each different meal, not including any sunk costs The optimal amounts of each meal to produce (in kg's) for its next batch of orders The amounts of each material (in kg's) to go into each kg of each different meal The amounts of time (in hours) required to prepare each kg of each different meal The amounts of each material (in kg's) that are available for producing the next batch of meals The amounts of time (in hours) that are available for producing the next batch of meals in each of the 3 departments the business currently has available The minimum amounts (in kg's) of each type of meal that need to be prepared The amounts of each of the materials and the amounts of time actual used The sensitivity report produced by Solver . . . When answering the following questions, you are to assume that every meal that is prepared is sold and that the following costs are either sunk or relevant as follows: . The material costs per kg are $5 for material 1, $6 for material 2 and $4 for material 3 and that these costs are sunk costs because all the available material must be paid for in advance The labour costs per hour are $6.00 and these costs are relevant costs in that the caterer only pays for the hours needed. When answering each of the following questions, if there is not enough information to answer the question, state that there is 'not enough info' and briefly state why. In addition, if you can answer a question, show any calculations necessary for arriving at your answer. a) What is the optimal amounts of each meal (in kg) that should be produced and what is the total profit (excluding sunk costs) b) Which constraints are binding? c) After producing all the meals, how much of material 3 is left over? d) If the minimum requirement for meal B was decreased by 4kg, what would be the change in total profit (excluding sunk costs)? meal A B profit/kg (excluding sunk costs) Optimal amounts of each meal (kg) $20 64.53 $18 7.00 $14 15.00 $28 14.85 0.20 0.30 s 0.50 s constraints: amount of material 1 (per kg ofproduct) amount of material 2 (per kg ofproduct) amount of material 3 (per kg ofproduct) time in dept. X (hours per kg of product) time in dept. Y (hours per kg of product) time in dept. Z (hours per kg of product) s 0.25 0.45 0.30 0.20 0.25 0.30 0.10 0.15 0.05 0.50 0.30 0.20 0.15 0.10 0.20 used (LMS) 26.22 40.00 35.16 16.00 19.26 9.46 0.25 0.10 0.65 0.35 0.45 0.10 Available (RHS) 35 40 38 16 24 16 $ s s minimum amounts (kg) of each product) 15.00 7.00 15.00 8.00 Total Profit (excluding sunk costs) $2,042.36 Microsoft Excel 16.0 Sensitivity Report Reduced Cost Name meal A meal B meal C meal D Final Value 64.53 7.00 15.00 14.85 0.00 0.00 0.00 0.00 Objective Allowable Allowable Coefficient Increase Decrease 20.00 120.00 8.33 18.00 10.18 infinite 14.00 4.55 infinite 28.00 42.00 13.44 Name minimum of meal A minimum of meat B minimum of meal C minimum of meal D amount of material 1 amount of material 2 amount of material 3 time in dept. X time in dept. Y time in dept. Z Final Value 64.53 7.00 15.00 14.85 26.22 40.00 35.16 16.00 19.26 9.46 Shadow Price 0.00 -10.18 -4.55 0.00 0.00 25.45 0.00 72.73 0.00 0.00 Constraint Allowable Allowable R.H. Side Increase Decrease 15.00 49.53 infinite 7.00 9.04 7.00 15.00 25.11 15.00 8.00 6.85 infinite 35.00 infinite 8.78 40.00 11.30 23.35 38.00 infinite 2.84 16.00 1.59 2.26 24.00 infinite 4.74 16.00 infinite 6.54