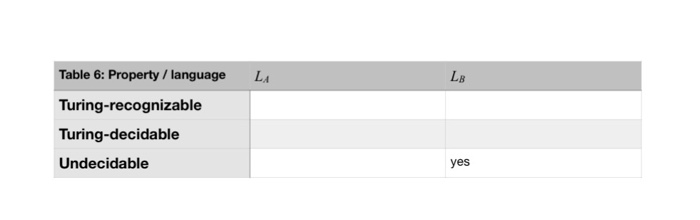
Question 4 (6 marks). In class we discussed the concept of reduction for the purpose of using this technique for proving that a language is undecidable To reduce a language LA to a language LB, one is to give an algorithm M that for any string x outputs a string y such that "x E L?" can be concluded from an answer to "y E LB?". Consider the following scenarios for reduction M from La to LB (Tables 1-6). For in each blank cell fill in either 'yes' or 'no'. Here, 'yes' means that, given the condition specified in the non- blank cell, one can conclude in all cases that Li satisfies the property specified; 'no' means that one cannot conclude in all cases that Li satisfies the property specified. (To be more specific, consider the first table below. Here we know that Ls is a a Turing-recognizable language. That is, LA can be any Turing-recognizable language We also know that there exists a reduction from LA to LB. To enter 'yes' or 'no' in the blank cell below the 'yes', you have to figure out whether or not you can conclude from that information that LA is Turing-decidable. To enter 'yes' or 'no'in the cell to the right of 'yes', one you have to figure out whether or not you can conclude from that information that LB is Turing-recognizable also.) Question 4 (6 marks). In class we discussed the concept of reduction for the purpose of using this technique for proving that a language is undecidable To reduce a language LA to a language LB, one is to give an algorithm M that for any string x outputs a string y such that "x E L?" can be concluded from an answer to "y E LB?". Consider the following scenarios for reduction M from La to LB (Tables 1-6). For in each blank cell fill in either 'yes' or 'no'. Here, 'yes' means that, given the condition specified in the non- blank cell, one can conclude in all cases that Li satisfies the property specified; 'no' means that one cannot conclude in all cases that Li satisfies the property specified. (To be more specific, consider the first table below. Here we know that Ls is a a Turing-recognizable language. That is, LA can be any Turing-recognizable language We also know that there exists a reduction from LA to LB. To enter 'yes' or 'no' in the blank cell below the 'yes', you have to figure out whether or not you can conclude from that information that LA is Turing-decidable. To enter 'yes' or 'no'in the cell to the right of 'yes', one you have to figure out whether or not you can conclude from that information that LB is Turing-recognizable also.)